精品解析：浙江省金华市婺城区八年级上学期期末数学试题

第一学期调研抽测试题卷

八年级数学

考生须知：

1．全卷共三大题，24小题，满分为120分．考试时间为120分钟，本次考试采用闭卷形式．

2．全卷分试卷Ⅰ（选择题）和试卷Ⅱ（非选择题）两部分，全部在答题纸上作答．卷Ⅰ的答案必须用2B铅笔填涂；卷Ⅱ的答案必须用黑色字迹钢笔或签字笔写在答题纸相应位置上．

3．请用黑色字迹钢笔或签字笔在“答题纸”上填写姓名和准考证号．

4．作图时，可先使用2B铅笔，确定后必须使用黑色字迹的钢笔或签字笔涂黑．

5．本次考试不得使用计算器．

卷Ⅰ

说明：本卷共有1大题，10小题，共30分．请用2B铅笔在答题纸上将你认为正确的选项对应的小方框涂黑、涂满．

一、选择题（本题有10小题，每小题3分，共30分）

1. 在平面直角坐标系中，点位于　　

A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限

2. 下列四个数字图形，是轴对称图形的是（    ）．

A.  B.  C.  D.

3. 一个不等式的解在数轴上表示如图，则这个不等式可以是（    ）

A.  B.  C.  D.

4. 线段首尾顺次相接组成三角形，若，则的长度可以是（    ）

A. 3 B. 4 C. 5 D. 6

5. 等腰三角形的底角为50°，则它的顶角度数是（　　）

A. 50° B. 80° C. 65°或80° D. 50°或80°

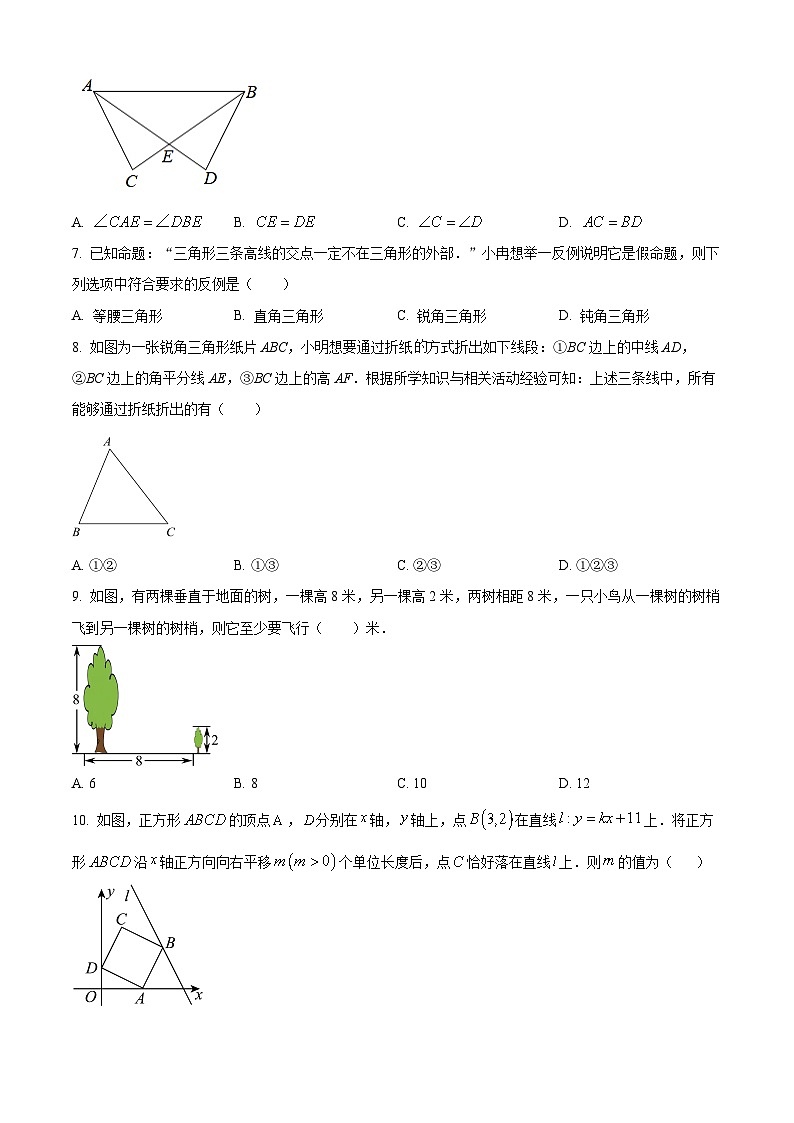
6. 如图，，添加下列条件，不能使的是（    ）

A.  B.  C.  D.

7. 已知命题：“三角形三条高线的交点一定不在三角形的外部．”小冉想举一反例说明它是假命题，则下列选项中符合要求的反例是（　　）

A. 等腰三角形 B. 直角三角形 C. 锐角三角形 D. 钝角三角形

8. 如图为一张锐角三角形纸片ABC，小明想要通过折纸方式折出如下线段：①BC边上的中线AD，②BC边上的角平分线AE，③BC边上的高AF．根据所学知识与相关活动经验可知：上述三条线中，所有能够通过折纸折出的有（　　）

A. ①② B. ①③ C. ②③ D. ①②③

9. 如图，有两棵垂直于地面的树，一棵高8米，另一棵高2米，两树相距8米，一只小鸟从一棵树的树梢飞到另一棵树的树梢，则它至少要飞行（　　）米．

A. 6 B. 8 C. 10 D. 12

10. 如图，正方形的顶点，分别在轴，轴上，点在直线上．将正方形沿轴正方向向右平移个单位长度后，点恰好落在直线上．则的值为（    ）

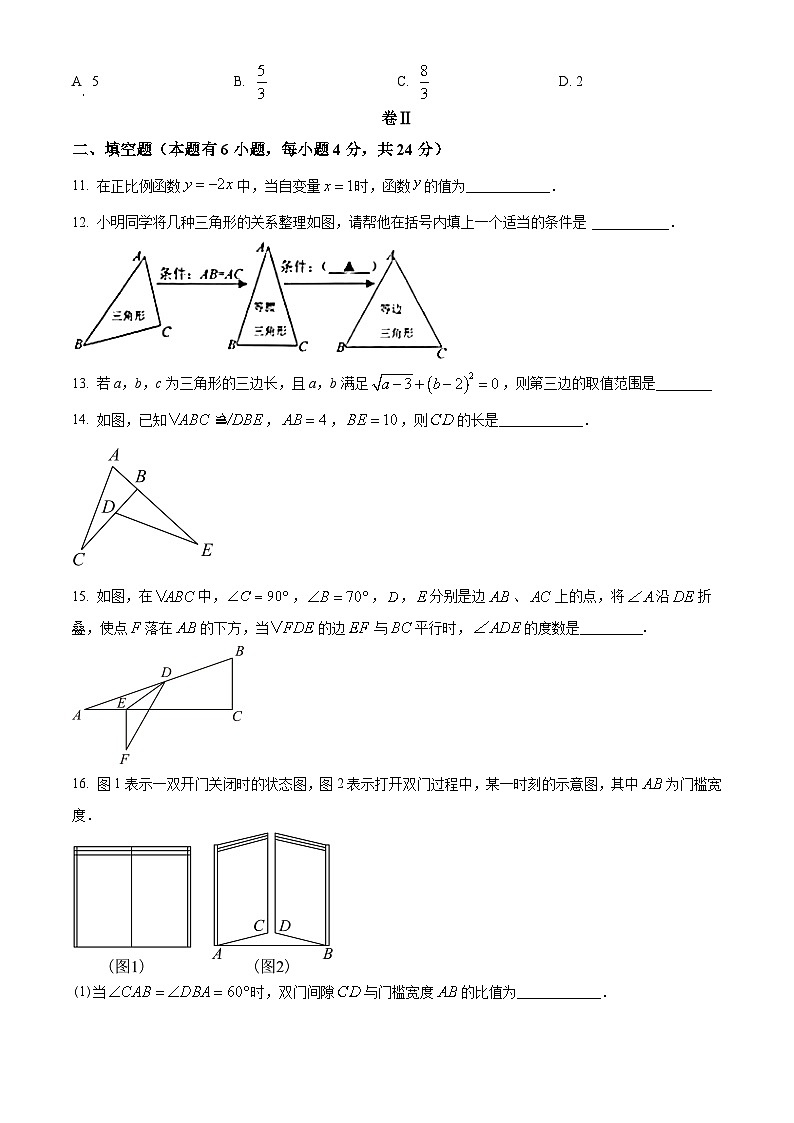
A 5 B.  C.  D. 2

卷Ⅱ

二、填空题（本题有6小题，每小题4分，共24分）

11. 在正比例函数中，当自变量时，函数的值为____________．

12. 小明同学将几种三角形的关系整理如图，请帮他在括号内填上一个适当的条件是 ___________．

13. 若a，b，c为三角形的三边长，且a，b满足，则第三边的取值范围是________

14. 如图，已知，，，则的长是____________．

15. 如图，在中，，，，分别是边、上的点，将沿折叠，使点落在的下方，当的边与平行时，的度数是_________．

16. 图1表示一双开门关闭时的状态图，图2表示打开双门过程中，某一时刻的示意图，其中为门槛宽度．

(1)当时，双门间隙与门槛宽度的比值为____________．

(2)若双门间隙的距离为寸，点和点距离都为尺(尺寸)，则门槛宽度是____________寸．

三、解答题（本题有8小题，共66分）

17. 解不等式组．

18 如图，，．求证：．

19. 如图，在的方格纸中，点，在格点上．请按要求画出格点线段（线段的端点在格点上），并写出结论．

（1）在图1中画一条平行于，且与相等的线段．

（2）在图2中画一条与垂直的线段．

（3）在图3中画一条平分的线段．

20. 如图，在涪江笔直的河流一侧有一旅游地C，河边有两个景点A、B．其中，因C到A的路不通，为方便游客决定在河边新建一个景点H（A、H、B三点在同一直线上），并新修一条路CH，测得千米，千米，千米．

（1）判断△BCH的形状，并说明理由；

（2）求原路线AC的长．

21. 为更好地推进生活垃圾分类工作，改善城市生态环境，某小区准备购买A、B两种型号的垃圾箱，通过对市场调研得知：购买3个A型垃圾箱和2个B型垃圾箱共需390元，购买2个A型垃圾箱比购买1个B型垃圾箱少用20元．

（1）求每个A型垃圾箱和每个B型垃圾箱分别多少元？

（2）该小区计划用不多于1500元的资金购买A、B两种型号的垃圾箱共20个，且A型号垃圾箱个数不多于B型垃圾箱个数的3倍，则该小区购买A、B两种型号垃圾箱的方案有哪些？

22. 某学校STEAM社团在进行项目化学习时，根据古代的沙漏模型（图1）制作了一套“沙漏计时装置”，该装置由沙漏和精密电子秤组成，电子秤上放置盛沙容器．沙子缓慢匀速地从沙漏孔漏到精密电子称上的容器内，可以通过读取电子秤的读数计算时间（假设沙子足够）．该实验小组从函数角度进行了如下实验探究：实验观察：实验小组通过观察，每两小时记录一次电子秤读数，得到表1．

表1

探索发现：

（1）建立平面直角坐标系，如图2，横轴表示漏沙时间x，纵坐标表示精密电子称的读数y，描出以表1中的数据为坐标的各点．

（2）观察上述各点的分布规律，判断它们是否在同一条直线上，如果在同一条直线上，请你建立适当的函数模型，并求出函数表达式，如果不在同一条直线上，请说明理由．结论应用：应用上述发现的规律估算：

（3）若漏沙时间为9小时，精密电子称的读数为多少？

（4）若本次实验开始记录的时间是上午7:30，当精密电子秤的读数为72克时是几点钟？

23. 定义：如果三角形有两个内角的差为60°，那么这样的三角形叫做“准等边三角形”．

（1）【理解概念】

顶角为120°的等腰三角形_____________“准等边三角形”．（填“是”或“不是”）

（2）【巩固新知】

已知是“准等边三角形”，其中，．求的度数．

（3）【解决问题】

如图，在中，，，，点在边上，若是“准等边三角形”，求的长．

24. 如图，直线与轴、轴分别交于点、点，点是射线上的动点，过点作直线的垂线交轴于点，垂足为点，连接．

（1）当点在线段上时，

①求证：；

②若点为中点，求的面积．

（2）在点运动过程中，是否存在某一位置，使得成为等腰三角形？若存在，求点的坐标；若不存在，请说明理由．