初中华师大版2 轴对称的再认识课后练习题

这是一份初中华师大版2 轴对称的再认识课后练习题，共11页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
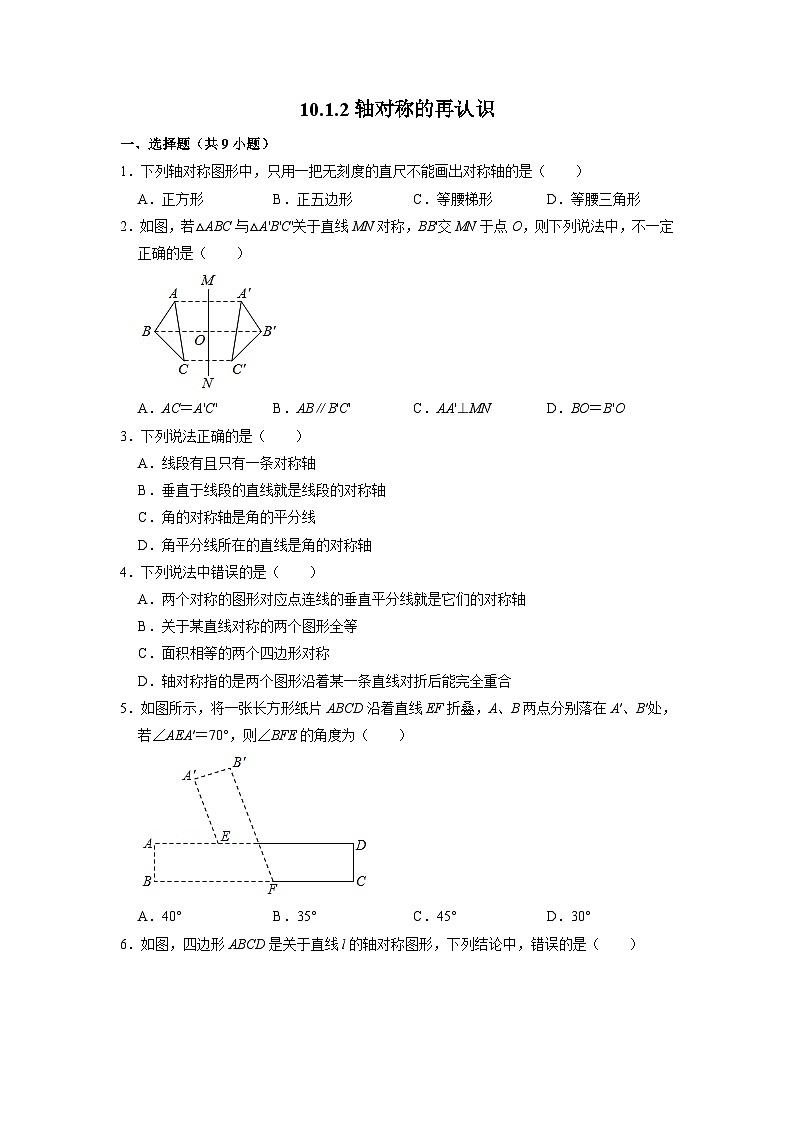
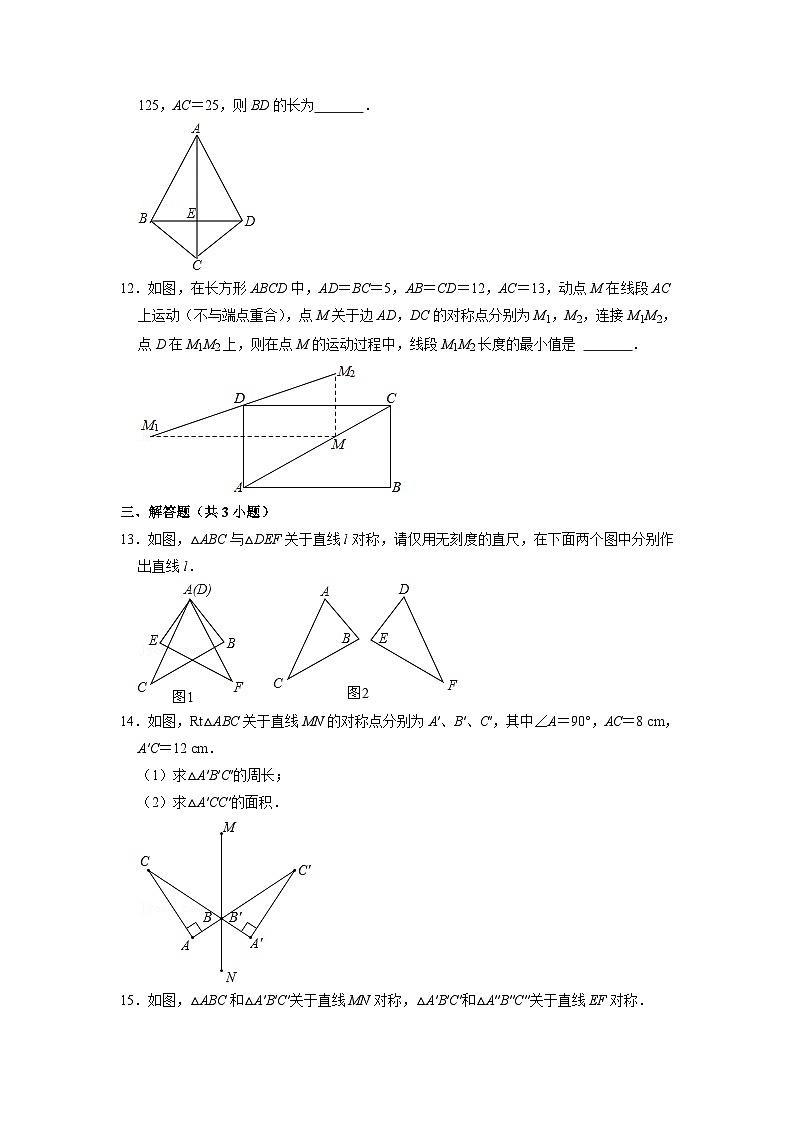
10.1.2轴对称的再认识一、选择题（共9小题）1．下列轴对称图形中，只用一把无刻度的直尺不能画出对称轴的是（　　）A．正方形 B．正五边形 C．等腰梯形 D．等腰三角形2．如图，若△ABC与△A'B'C'关于直线MN对称，BB'交MN于点O，则下列说法中，不一定正确的是（　　）A．AC＝A'C' B．AB∥B'C' C．AA'⊥MN D．BO＝B'O3．下列说法正确的是（　　）A．线段有且只有一条对称轴 B．垂直于线段的直线就是线段的对称轴 C．角的对称轴是角的平分线 D．角平分线所在的直线是角的对称轴4．下列说法中错误的是（　　）A．两个对称的图形对应点连线的垂直平分线就是它们的对称轴 B．关于某直线对称的两个图形全等 C．面积相等的两个四边形对称 D．轴对称指的是两个图形沿着某一条直线对折后能完全重合5．如图所示，将一张长方形纸片ABCD沿着直线EF折叠，A、B两点分别落在A′、B′处，若∠AEA′＝70°，则∠BFE的角度为（　　）A．40° B．35° C．45° D．30°6．如图，四边形ABCD是关于直线l的轴对称图形，下列结论中，错误的是（　　）A．AD＝BC B．AD⊥BC C．AC，BD的交点在L上 D．直线AD，BC的交点在L上7．如图，△ABC中，∠ACB＝90°，沿CD折叠△CBD，使点B恰好落在AC边上的点E处．若∠A＝22°，则∠BDC等于（　　）A．44° B．60° C．67° D．77°8．如图，将一个三角形纸片ABC沿过点B的直线折叠，使点C落在AB边上的点E处，折痕为BD，则下列结论一定正确的是（　　）A．AD＝BD B．BE＝AC C．ED+EB＝DB D．AE+CB＝AB9．如图，将矩形纸片ABCD沿BE折叠，使点A落在对角线BD上的A′处．若∠DBC＝24°，则∠A′EB等于（　　）A．24° B．33° C．57° D．66°二、填空题（共4小题）10．如图，将△ABC折叠，使点A与BC边中点D重合，折痕为MN，若AB＝9，BC＝6，则△DNB的周长为　   　．11．如图，△ABC与△ADC关于直线AC对称，连接BD，若已知四边形ABCD的面积是125，AC＝25，则BD的长为　   　．12．如图，在长方形ABCD中，AD＝BC＝5，AB＝CD＝12，AC＝13，动点M在线段AC上运动（不与端点重合），点M关于边AD，DC的对称点分别为M1，M2，连接M1M2，点D在M1M2上，则在点M的运动过程中，线段M1M2长度的最小值是 　   　．三、解答题（共3小题）13．如图，△ABC与△DEF关于直线l对称，请仅用无刻度的直尺，在下面两个图中分别作出直线l．14．如图，Rt△ABC关于直线MN的对称点分别为A′、B′、C′，其中∠A＝90°，AC＝8 cm，A′C＝12 cm．（1）求△A′B′C′的周长；（2）求△A′CC′的面积．15．如图，△ABC和△A′B′C′关于直线MN对称，△A′B′C′和△A″B″C″关于直线EF对称．（1）画出直线EF，并写出作法；（2）直线MN与EF相交于点O，试探究∠BOB″与直线MN，EF所夹锐角α的数量关系．
10.1.2轴对称的再认识参考答案与试题解析一、选择题（共9小题）1．下列轴对称图形中，只用一把无刻度的直尺不能画出对称轴的是（　　）A．正方形 B．正五边形 C．等腰梯形 D．等腰三角形【解答】解：A、正方形，对角线所在的直线即为对称轴，可以用直尺画出，故A选项错误；B、正五边形，作一条对角线把正五边形分成一等腰三角形与以等腰梯形，根据正五边形的对称性，过等腰三角形的顶点与梯形的对角线的交点的直线即为对称轴，故B选项错误；C、等腰梯形，延长两腰相交于一点，作两对角线相交于一点，根据等腰梯形的对称性，过这两点的直线即为对称轴，故C选项错误；D、等腰三角形，只用一把无刻度的直尺无法画出，故D选项正确．故选：D．2．如图，若△ABC与△A'B'C'关于直线MN对称，BB'交MN于点O，则下列说法中，不一定正确的是（　　）A．AC＝A'C' B．AB∥B'C' C．AA'⊥MN D．BO＝B'O【解答】解：∵△ABC与△A'B'C'关于直线MN对称，∴AC＝A′C′，AA′⊥MN，BO＝OB′，故选项A，C，D正确，故选：B．3．下列说法正确的是（　　）A．线段有且只有一条对称轴 B．垂直于线段的直线就是线段的对称轴 C．角的对称轴是角的平分线 D．角平分线所在的直线是角的对称轴【解答】解：A、根据线段有两条对称轴，故此选项错误；B、根据垂直平分线段的直线就是线段的对称轴，故此选项错误；C、根据角的对称轴是角的平分线所在直线，故此选项错误；D、根据角平分线所在的直线是角的对称轴，故此选项正确；故选：D．4．下列说法中错误的是（　　）A．两个对称的图形对应点连线的垂直平分线就是它们的对称轴 B．关于某直线对称的两个图形全等 C．面积相等的两个四边形对称 D．轴对称指的是两个图形沿着某一条直线对折后能完全重合【解答】解：A、B、D都正确；C、面积相等的两个四边形不一定全等，故不一定轴对称，错误．故选：C．5．如图所示，将一张长方形纸片ABCD沿着直线EF折叠，A、B两点分别落在A′、B′处，若∠AEA′＝70°，则∠BFE的角度为（　　）A．40° B．35° C．45° D．30°【解答】解：由平行线的性质得，∠AEA'＝∠1＝70°，∵AD∥BC，∴∠1＝∠BFB'＝70°，由折叠性质得，∠BFE＝∠EFB'＝∠BFB'＝35°，故选：B．6．如图，四边形ABCD是关于直线l的轴对称图形，下列结论中，错误的是（　　）A．AD＝BC B．AD⊥BC C．AC，BD的交点在l上 D．直线AD，BC的交点在l上【解答】解：A、四边形ABCD是关于直线l的轴对称图形，必有AD＝BC，正确；B、AD、BC与l的夹角相等，但不一定垂直，错误；C、AC，BD的交点在l上，正确；D、直线AD，BC的交点在l上，正确．故选：B．7．如图，△ABC中，∠ACB＝90°，沿CD折叠△CBD，使点B恰好落在AC边上的点E处．若∠A＝22°，则∠BDC等于（　　）A．44° B．60° C．67° D．77°【解答】解：△ABC中，∠ACB＝90°，∠A＝22°，∴∠B＝90°﹣∠A＝68°，由折叠的性质可得：∠CED＝∠B＝68°，∠BDC＝∠EDC，∴∠ADE＝∠CED﹣∠A＝46°，∴∠BDC＝＝67°．故选：C．8．如图，将一个三角形纸片ABC沿过点B的直线折叠，使点C落在AB边上的点E处，折痕为BD，则下列结论一定正确的是（　　）A．AD＝BD B．BE＝AC C．ED+EB＝DB D．AE+CB＝AB【解答】解析：∵△BDE是由△BDC翻折而成，∴BE＝BC，∵AE+BE＝AB，∴AE+CB＝AB，故D正确，无法得出AD＝CD，AE＝AD，AD＝DE，故选：D．9．如图，将矩形纸片ABCD沿BE折叠，使点A落在对角线BD上的A′处．若∠DBC＝24°，则∠A′EB等于（　　）A．24° B．33° C．57° D．66°【解答】解：∵四边形ABCD是矩形，∴∠A＝∠ABC＝90°，AD∥BC，由折叠的性质得：∠BA'E＝∠A＝90°，∠A'BE＝∠ABE，∵AD∥BC，∴∠ADB＝∠DBC＝24°，∴∠A'BE＝∠ABE＝（90°﹣∠ADB）＝（90°﹣24°）＝33°，∴∠A'EB＝90°﹣∠A'BE＝90°﹣33°＝57°．故选：C．二、填空题（共4小题）10．如图，将△ABC折叠，使点A与BC边中点D重合，折痕为MN，若AB＝9，BC＝6，则△DNB的周长为　12　．【解答】解：∵D为BC的中点，且BC＝6，∴BD＝BC＝3，由折叠性质知NA＝ND，则△DNB的周长＝ND+NB+BD＝NA+NB+BD＝AB+BD＝3+9＝12，故答案为：12．11．如图，△ABC与△ADC关于直线AC对称，连接BD，若已知四边形ABCD的面积是125，AC＝25，则BD的长为　10　．【解答】解：∵△ABC与△ADC关于直线AC对称，∴△ABC与△ADC的面积相等；四边形ABCD的面积等于△ABC与△ADC的面积之和；四边形ABCD的面积＝AC×BD＝125AC＝25，则BD＝10．12．如图，在长方形ABCD中，AD＝BC＝5，AB＝CD＝12，AC＝13，动点M在线段AC上运动（不与端点重合），点M关于边AD，DC的对称点分别为M1，M2，连接M1M2，点D在M1M2上，则在点M的运动过程中，线段M1M2长度的最小值是 　　．【解答】解：过D作DM'⊥AC于M'，连接DM，如图：长方形ABCD中，AD＝BC＝5，AB＝CD＝12，AC＝13，∴S△ADC＝AD•CD＝AC•DM'，∴DM'＝＝，∵M关于边AD，DC的对称点分别为M1，M2，∴DM1＝DM＝DM2，∴M1M2＝2DM，线段M1M2长度最小即是DM长度最小，此时DM⊥AC，即M与M'重合，M1M2最小值为2DM'＝．故答案为：．三、解答题（共3小题）13．如图，△ABC与△DEF关于直线l对称，请仅用无刻度的直尺，在下面两个图中分别作出直线l．【解答】解：如图所示．14．如图，Rt△ABC关于直线MN的对称点分别为A′、B′、C′，其中∠A＝90°，AC＝8cm，A′C＝12 cm．（1）求△A′B′C′的周长；（2）求△A′CC′的面积．【解答】解：（1）∵Rt△ABC关于直线MN的对称点分别为A′、B′、C′，AC＝8cm，A′C＝12cm，∴AB＝A′B′，BC＝B′C′，∴△A′B′C′的周长为：A′C′+B′C′+A′B′＝A′C+AC＝12+8＝20（cm）； （2）由（1）得：△A′CC′的面积为：A′C×A′C′＝×12×8＝48（cm2）．15．如图，△ABC和△A′B′C′关于直线MN对称，△A′B′C′和△A″B″C″关于直线EF对称．（1）画出直线EF，并写出作法；（2）直线MN与EF相交于点O，试探究∠BOB″与直线MN，EF所夹锐角α的数量关系．【解答】解：（1）作法：连接B′B″，作线段B′B″的垂直平分线EF． （2）连接B′O，则α＝∠MOB′+∠B′OE，∠BOB″＝∠BOM+∠MOB′+∠B′OE+∠EOB″．又因为△ABC与△A′B′C′关于直线MN对称，△A′B′C′与△A″B″C″关于直线EF对称，所以∠BOM＝∠MOB′，∠B′OE＝∠EOB″，所以∠BOB″＝2∠MOB′+2∠B′OE，所以∠BOB″＝2α．