数学九年级上册21.2.1 配方法教学演示课件ppt

这是一份数学九年级上册21.2.1 配方法教学演示课件ppt，共20页。PPT课件主要包含了19x2＝1，a＋b，a－b，你发现了什么规律，配方的关键，x2＋4x＋1＝0，x2＋4x＝－1，两边都加上4，x＋22＝3等内容，欢迎下载使用。

1．理解配方法的概念．2．能够用配方法解一元二次方程及解决有关问题．3．探索直接开平方法和配方法之间的区别与联系．
（2）(x－2)2＝2．
1．用直接开平方法解下列方程：
2．你还记得完全平方公式吗？填一填：
（1）a2＋2ab＋b2＝( )2；
（2）a2－2ab＋b2＝( )2．
下列方程能用直接开平方法来解吗?
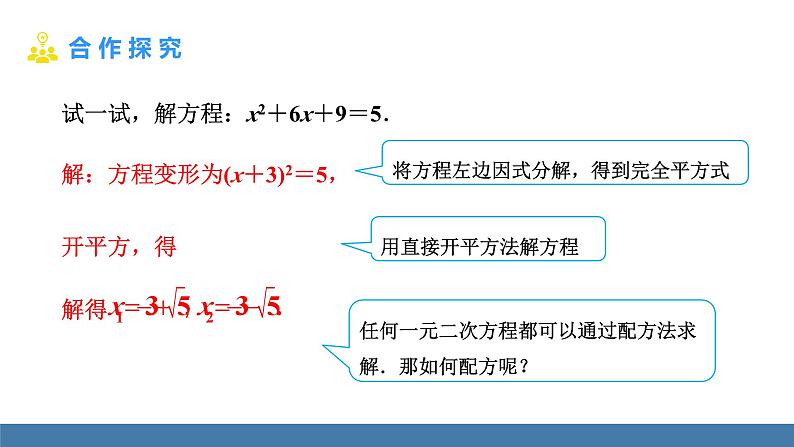
（1）x2＋6x＋9＝5；
（2）x2＋4x＋1＝0．
解：方程变形为(x＋3)2＝5，
试一试，解方程：x2＋6x＋9＝5．
将方程左边因式分解，得到完全平方式
任何一元二次方程都可以通过配方法求解．那如何配方呢？
填上适当的数或式，使下列各等式成立．
（1）x2＋4x＋ ＝(x＋ )2；
（2）x2－6x＋ ＝(x－ )2；
（3）x2＋8x＋ ＝(x＋ )2；
x2－ x＋ ＝(x－ )2．
对于二次项系数为1的二次三项式，将常数项配成一次项系数一半的平方时，可得完全平方式．
把握二次项系数为1的完全平方式的特点：常数项等于一次项系数一半的平方．
想一想 怎样解方程x2＋4x＋1＝0? (I)
问题1 能不能将方程(I)变成(x＋n)2＝p的形式呢？
x2＋4x＋4＝－1＋4
为什么在方程x2＋4x＝－1的两边加上4？加其他的数，行吗？
左边写成完全平方的形式
通过配成完全平方形式来解一元二次方程的方法，叫做配方法．
配方法解一元二次方程的基本思路
把方程化为(x＋n)2＝p的形式，再运用直接开平方法降次，转化为两个一元一次方程求解．
解：（1）移项，得x2－8x＝－1．　　　　　　
例1 解下列方程：（1）x2－8x＋1＝0；　　（2）2x2＋1＝3x；　　（3）3x2－6x＋4＝0．
配方，得x2－8x＋42＝－1＋42，
即(x－4)2＝15．
解：（2）移项，得2x2－3x＝－1．
解：（3）移项，得3x2－6x＝－4．　　
因为实数的平方不会是负数，所以x取任何实数时，(x－1)2都是非负数，上式不成立，即原方程无实数根．　　　　
注意：在(x＋n)2＝p中，只有当p≥0时，才能直接开平方，p＜0时，直接下结论：方程无实数根．
用配方法解一元二次方程的一般步骤：
例2 用配方法求最值．（1）2x2－4x＋5的最小值；　（2）－3x2＋6x－7的最大值．
解：（1）原式＝2(x－1)2＋3．当x＝1时，有最小值3．
（2）原式＝－3(x－1)2－4．当x＝1时，有最大值－4．
ax2＋bx＋c(a，b，c均为常数)型代数式求最值或证明恒为正（负）等问题时，都要想到运用配方法，将含字母部分配成a(x＋m)2＋n的形式来解决．
例3 若a，b，c为△ABC的三边长，且试判断△ABC的形状．
∴△ABC为直角三角形．
1．方程x2－4＝0的解是（　　）A．x＝2　　　　B．x＝－2　　　　C．x＝±2　　　　D．x＝±42．方程2x2－3m－x＋m2＋2＝0有一根为x＝0，则m的值为（　　）A．1　　　　 B．1 C．1或2 D．1或－2
3．解方程：(x＋1)(x－1)＋2(x＋3)＝8．
解：方程化简，得x2＋2x＋5＝8．移项，得x2＋2x＝3．配方，得x2＋2x＋1＝3＋1，即(x＋1)2＝4．开平方，得x＋1＝±2．解得x1＝1，x2＝－3．
4．用配方法解x2－4x＝1．
5．解方程：3x2＋8x－3＝0．