人教版九年级上册23.2.1 中心对称教学演示ppt课件

这是一份人教版九年级上册23.2.1 中心对称教学演示ppt课件，共26页。PPT课件主要包含了特别提醒等内容，欢迎下载使用。
1.理解中心对称的定义.2.探究中心对称的性质.3.能利用中心对称的性质作图.
前面我们研究了旋转及其性质，现在研究一类特殊的旋转——中心对称及其性质.
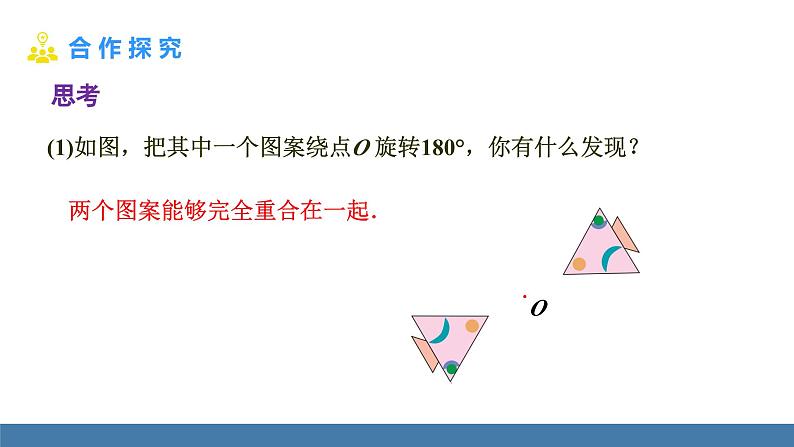
(1)如图，把其中一个图案绕点O 旋转180°，你有什么发现？
两个图案能够完全重合在一起．
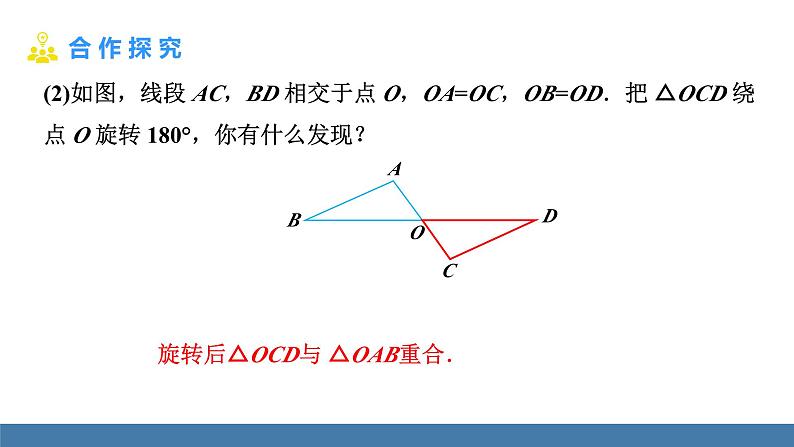
(2)如图，线段 AC，BD 相交于点 O，OA=OC，OB=OD．把 △OCD 绕点 O 旋转 180°，你有什么发现？
旋转后△OCD与 △OAB重合．
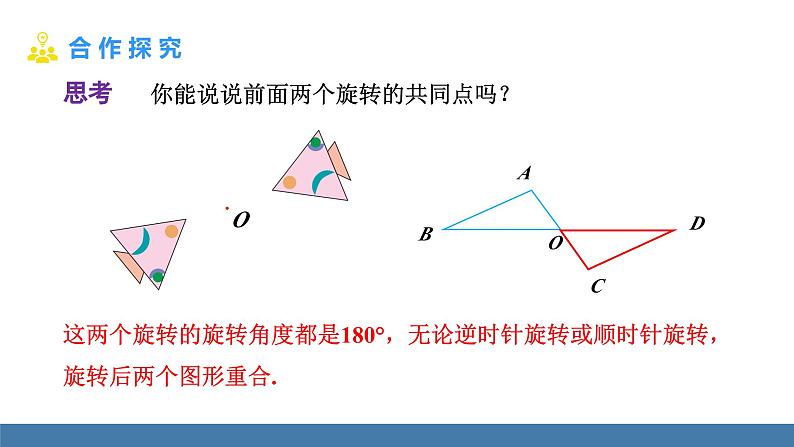
你能说说前面两个旋转的共同点吗？
这两个旋转的旋转角度都是180°，无论逆时针旋转或顺时针旋转，旋转后两个图形重合.
定义：把一个图形绕着某一点旋转 180º，如果它能够与另一个图形重合，那么就说这两个图形关于这个点对称或中心对称，这个点叫做对称中心. 这两个图形在旋转后能重合的对应点叫做关于对称中心的对称点.
特别提醒1.中心对称是指两个图形的位置关系，必须涉及两个图形.2.中心对称的两个图形，只有一个对称中心.这个对称中心可能在每个图形的外部，也可能在每个图形的内部或边上.3.中心对称是特殊的旋转，旋转角为180°.
如图，旋转三角尺，画出关于点O对称的两个三角形：第一步，画出△ABC；第二步，以三角板的一个顶点为中心O ，把三角尺旋转 180°，画出△A′B′C′；第三步，移开三角尺.
这样画出的 △ABC 与 △A′B′C′ 关于点 O 对称，点 O 在线段 AA′上吗？如果在，在什么位置？猜测：△ABC 与△A′B′C′ 有什么关系？
猜测：△ABC ≌ △A′B′C′.
点O是线段AA′的中点.
∵点A′是点A绕点O旋转180°得到的,∴点O在线段AA′上，且OA=OA′,同样地，点O也是线段BB′和CC′的中点.在△AOB与△A′OB′中, OA = OA′，OB = OB′，∠AOB =∠A′OB′， ∴△AOB ≌ △A′OB′.∴AB=A′B′.同理 BC=B′C′，AC=A′C′. ∴ △ABC ≌ △A′B′C′.
说明△ABC ≌ △A′B′C′.
中心对称的性质1.中心对称的两个图形，对称点所连线段都经过对称中心，而且被对称中心平分. 2.中心对称的两个图形是全等图形.
因为中心对称是一种特殊的旋转变换，所以具备旋转的一切性质.成中心对称的两个图形，其对应线段互相平行(或在同一条直线上)且相等.
例1 (1)如图1，选择点O为对称中心，画出点A关于O点的对称点A'；
解：如图，连接AO，在AO的延长线上截取OA′=OA，即可以求得点A关于点O的对称点 A′.
(2)如图2，选择点O为对称中心，画出与△ABC关于点O对称的△A'B'C'.
解：如图，作出 A，B，C 三点关于点 O 的对称点 A'，B'，C'，顺次连接A'B'，B'C'，C'A'，则△A'B'C'即为所作.
例2 如图，已知△ABC与△A′B′C′成中心对称，找出它们的对称中心 O.
解法1：根据观察，B，B′应是对应点，连接BB′，用刻度尺找出BB′的中点O，则点O即为所求（如图）.
解法2：根据观察，B，B′及C、C′应是两组对应点，连接BB′、CC′，BB′、CC′相交于点O，则点O即为所求（如图）.
1.已知四边形ABCD 的中心对称图形是四边形A1B1C1D1，请回答下列问题：(1)点A 的对称点是点______， 点B 的对称点是点______，对称中心是点______ .(2)指出图中在同一条直线上的三点.
解：A，O，A1；B，O，B1；C，O，C1；D，O，D1.
1.已知四边形ABCD 的中心对称图形是四边形A1B1C1D1，请回答下列问题：(3)指出图中相等的线段和全等的三角形.
解：图中相等的线段有OA=OA1，OB=OB1，OC=OC1，OD=OD1，AB=A1B1，BC=B1C1，CD=C1D1，DA=D1A1；全等的三角形有△ ABO 与△ A1B1O，△ ADO 与△ A1D1O，△ BCO 与△ B1C1O，△ DCO 与△ D1C1O.
2.如图，两个五角星关于某一点成中心对称，指出哪一点是对称中心，并指出图中点A，B，C，D 的对称点.
解：从图中易看出旋转中心为点A，故点A为对称中心；点A，B，C，D 绕点A 旋转180°后的位置分别在点A，G，H，E 处，故点A，B，C，D 关于点A 的对称点分别是点A，G，H，E.
3.如图，已知四边形ABCD 和点O，画四边形A′B′C′D′，使四边形A′B′C′D′与四边形ABCD 关于点O 成中心对称．
解：(1)连接AO 并延长AO 到A′，使OA′ = OA，于是得到点A 关于点O 的对称点A′ .(2)同样画出点B，C 和点D 关于点O 的对称点B′，C ′和D′．(3)连接A′B′，B′C′，C′D′，D′A′，则四边形A′B′C′D′即为所求作的图形．