人教版九年级数学上册课件 24.3 正多边形和圆

这是一份人教版九年级数学上册课件 24.3 正多边形和圆，共29页。

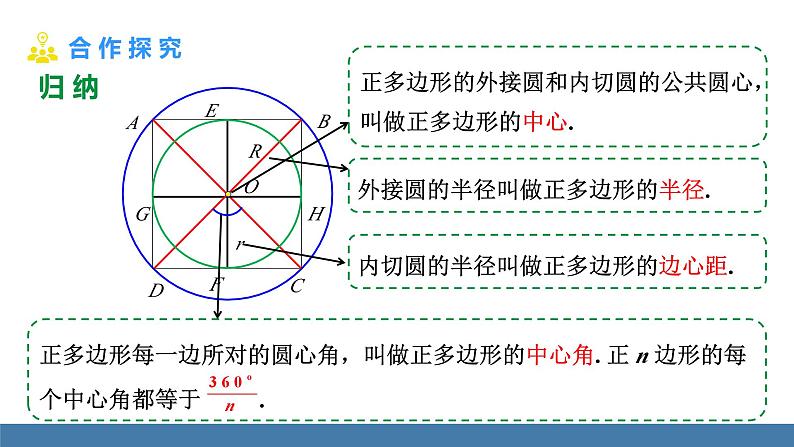
24.3　正多边形和圆1. 了解正多边形和圆的有关概念.2. 理解并掌握正多边形半径、中心角、边心距、边长之间的关系. 3. 会应用正多边形和圆的有关知识解决实际问题.各边相等、各角也相等的多边形是正多边形.利用正多边形，可以得到许多美丽的图案.你能找出下面各个图形中用到的正多边形吗？问题1 什么叫做正多边形？各边相等，各角也相等的多边形叫做正多边形.矩形不是正多边形，因为矩形不符合各边相等；菱形不是正多边形，因为菱形不符合各角相等.问题2 矩形是正多边形吗？为什么？菱形是正多边形吗？为什么？探 究正多边形和圆的关系非常密切，只要把一个圆分成相等的一些弧，就可以作出这个圆的内接正多边形，这个圆就是这个正多边形的外接圆.接下来，以圆内接正五边形为例证明.把⊙O 分成相等的5段弧，依次连接各分点得到五边形ABCDE.·AOEDCB五边形 ABCDE 是正五边形吗？简单说说理由.把圆分成n(n ≥ 3)等份，依次连接各分点得到的多边形就是这个圆的内接正n 边形，这个圆就是这个正n 边形的外接圆.圆的内接正 n 边形 OABCDEFGHRr正多边形的外接圆和内切圆的公共圆心，叫做正多边形的中心.外接圆的半径叫做正多边形的半径.内切圆的半径叫做正多边形的边心距.归 纳所有的正多边形是不是都有一个外接圆和一个内切圆？任何正多边形都有一个外接圆和一个内切圆，并且这两个圆是同心圆.例1 如图，三角形AOB 是正三角形，以点O 为圆心，OA 为半径作⊙ O，直径FC ∥ AB，AO，BO 的延长线交⊙ O 于点D，E，求证：六边形ABCDEF 为圆内接正六边形.分析：紧扣正多边形的定义，结合同圆中弦、弧、圆心角的关系证明.证明一个多边形是圆内接正多边形1.利用正多边形的定义，证明圆内接多边形的每个内角相等，每条边相等；2. 证明圆内接多边形各边所对的弧相等，即证明这个多边形的各顶点等分这个圆.方 法 归 纳例2 有一个亭子，它的地基是半径为 4 m 的正六边形，求地基的周长和面积 ( 结果保留小数点后一位).CDOEFAB解：如图，连接OB，OC.因为六边形ABCDEF是正六边形，所以它的中心角为60°，△OBC是等边三角形，正六边形的边长等于它的半径.CDOEFAB因此，亭子地基的周长l=6×4=24(m).圆内接正多边形的辅助线特别提醒思 考正n边形的一个内角的度数是多少？中心角呢？正多边形的中心角与外角的大小有什么关系？60°120°120°90°90°90°120°60°60°正多边形的外角=中心角归 纳实际生活中，经常遇到画正多边形的问题，比如画一个六角螺帽的平面图，画一个五角星等，这些问题都与等分圆周有关.怎样画任意正n边形呢？将圆 n 等分，然后顺次连接各等分点，即得到所要作的正n 边形.思考：怎样等分圆？1. 用量角器等分圆在⊙ O 中，用直尺和圆规作两条互相垂直的直径，就可把圆周四等分，从而作出正方形，若再逐次平分各边所对的弧，就可以作边数逐次倍增的正多边形，如正八边形、正十六边形等.2. 用尺规等分圆对于一些特殊的正n 边形，如正方形、正八边形，可以用圆规和直尺作图. 如图 ② .1. 画圆内接正n边形，实质是找圆的 n 等分点.2. 用量角器等分圆是一种简单常用的方法，但边数很大时，容易产生较大误差.3. 尺规作图是一种比较准确的等分圆的方法，但只限于作一些特殊的正多边形.特 别 提 醒1.下列说法中，不正确的是(　　)A. 正多边形一定有一个外接圆和一个内切圆B. 各边相等且各角相等的多边形是正多边形C. 正多边形的内切圆和外接圆是同心圆D. 正多边形既是轴对称图形，又是中心对称图形D2.若一个四边形的外接圆与内切圆是同心圆，则这个四边形一定是( )A.矩形 B. 菱形C. 正方形 D. 不能确定A3.一元钱硬币的直径约为 24 mm，则用它能完全覆盖住的正六边形的边长最大不能超过 (　　)A. 12 mm B. 12 mmC. 6 mm D. 6 mmA4.如图，正五边形 ABCDE 内接于⊙O，则∠ADE 的度数是( ) A．60° B．45° C．36° D．30° C解析：由五边形 ABCDE 是正五边形且内接于⊙O，可求出弧 AE 所对的圆心角的度数等于 360°÷5 = 72°，再根据圆周角定理可得到∠ADE 的度数.5. 如图，已知点 O 是正六边形 ABCDEF 的对称中心，G，H 分别是 AF，BC 上的点，且 AG = BH．(1) 求∠FAB 的度数；(2) 求证：OG = OH．证明：连接 OA，OB，∵OA = OB，∴∠OAB =∠OBA.∵∠FAB =∠CBA，∴∠OAG =∠OBH.∴△AOG ≌△BOH（SAS）.∴OG = OH．正多边形和圆有关计算画法中心半径中心角边心距