2021北京北大附中高一（下）期末数学

2021北京北大附中高一下期末

数    学

注意事项

1．考试时间:90分钟；满分:100分。

2．所有试题答案都写在答题纸的规定位置超出范围无效。

3．使用黑色字迹的签字笔或钢笔答题，不得使用铅笔答题。不能使用涂改液、胶带纸、修正带修改。

4．只呈交答题纸，试卷自己留存。

I卷(共87分)

一、选择题：共6小题，每小题3分，共18分.在每小题的四个选项中，选出符合条件的一项。

1．在△ABC中，∠A=30°, AC=2, AB= , 则BC= (    )

A.   B.2   C.   D.3

2．已知复数,,则复数在复平面内所表示的点位于(    )

A.第一象限   B.第二象限  C.第三象限  D.第四象限

3．如右图，在正方体中，面对角线条数、体对角线条数、与AB异面的棱数分别为(    )

A.8，4，5   B.12，8，4

C.12，4，4   D.8，8，4

4．已知圆锥的轴截面是边长为1的等边三角形，则它的侧面展开图中圆心角大小为(    ).

A. π   B. (+1)π    C. π  D.

5．在△ABC中，内角A、B、C所对的边分别为a、b、c. 若a=4，b=5，则当c=(    )时，

△ABC是钝角三角形.

A.1    B.2    C.3  D.4

6．同为瓶装水，有些瓶子的下半部分可以大致地看成是正四棱柱(比如某哈哈)，还有一些瓶子的下半部分可以大致地看成是圆柱(比如一层诚信水站的某山泉)．从数学角度来看，不同的设计各有什么优点呢？现在考虑两个等高、且均无上底面的圆柱和正四棱柱．在正四棱柱中装满水后，再将正四棱柱中的水全部倒入圆柱中，发现这些水也恰好可以注满圆柱．则此正四棱柱和圆柱的底面积、表面积的关系为(    )

A.底面积相等、表面积相等; B.底面积相等、圆柱的表面积小;

C.底面积相等、圆柱的表面积大: D. 底面积和表面积都是正四棱柱比较小.

二、填空题：共6小题，每小题3分，共18分.

7．在△ABC中，c＝1, b＝，C＝，则B＝       ．

8．在△ABC中，a=7，b=4，c=，则△ABC中最小角的大小为        ，△ABC的面积为        ．

9．已知为i虚数单位，且复数z满足.则的最大值为        ．

10.异面直线的判定方法，

文字语言描述为：平面的一条交线与面内不经过交点的直线异面；

图形语言呈现为：

符号语言表达为：                                    ，则直线a与b异面．

11．已知正四棱锥S-ABCD中，底面边长为2，斜高为，则正四棱锥的体积为         ．

12．平面四边形ABCD中，AB=BC=CA=2,AD=DC，∠CDA= 90°，把三角形ABC沿AC折起，使得三角形ABC所在平面与三角形ACD所在平面垂直，连接BD，则直线BD与平面ACD所成角的余弦值为_____，点C到平面ABD的距离为        ．

三、解答题：共4小题，共51分，解答应写出文字说明，演算步骤或证明过程.

13．已知复数其中m∈R,

（1）若已知z为纯虚数，求m的值并求z的虚部；

（2）当m=2时，求；

（3）若，求实数m，x的值．

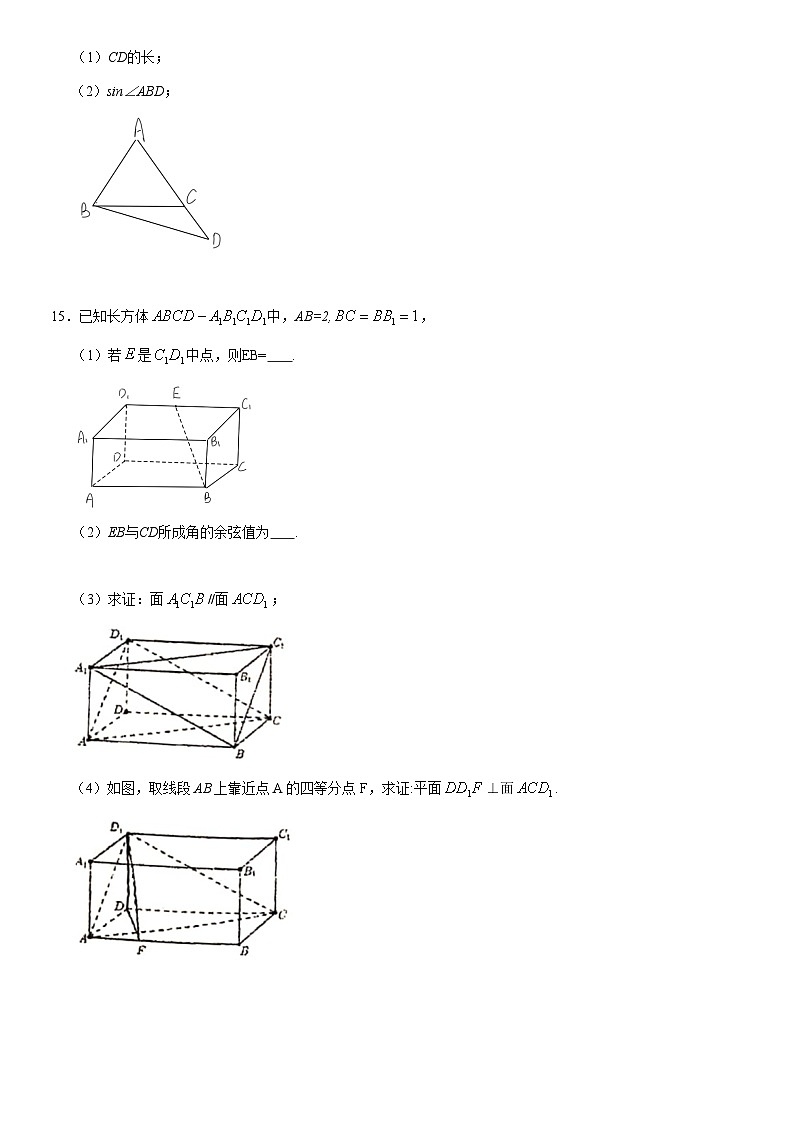
14．如图，△ABC是等边三角形，点D在边AC的延长线上，且AC=2CD，BD=,求

（1）CD的长；

（2）sin∠ABD；

15．已知长方体中，AB=2,，

（1）若是中点，则EB=       .

（2）EB与CD所成角的余弦值为       .

（3）求证：面//面；

（4）如图，取线段AB上靠近点A的四等分点F，求证:平面⊥面.

16．已知△ABC满足条件C＝，试从下列三条件① a＝c. ② cosB= ③ b=中再选出两个，

（1）若选出的两个条件与条件C＝的组合使得△ABC不存在，则选出的两个条件是             .

并说明理由.

（2）若选出的两个条件与条件C＝的组合使得△ABC存在且唯一，则选出的两个条件是             .

并求AB的长度.

II卷(共13分)

一、选择题：共2小题，每小题2分，其4分在每小题的四个选项中，远出符合条件的一项。

17．在△ABC中，若acosB-bcosA=c，则△ABC为(    )三角形.

A.锐角   B.直角   C.钝角   D.无法确定

18．如图，正方体的棱长为2,点O为底面ABCD的中心，点P在侧面的边界及其内部运动，且⊥,则△面积的最大值为(    ).

A.    B. 2 

C.   D.1

二、填空题：共2小题，每小题2分，共4分

19．在△ABC中，a=3，b=2，∠B=2∠A，则cosA=           ， c=          .

20．已知是各棱长均等于a的正三棱柱，D是侧棱的中点，则平面ABC与平面所成角的大小为         .

三、解答题(5分).

21.定义：球冠及其高；

球面与一个平面相交，被该平面截得的其中-个部分称为球冠，球与平面垂直的直径被平面分割的两条线段中，与球冠同侧的部分称为该球冠的高(如图)球冠的表面积，其中h为球冠的高，R为球半径。

2021年7月4日，中国天宫空间站宇航员首次执行了出舱活动，其中国首创的太空7轴智能机器臂起到了很好的辅助作用。多轴机器人，是以三维直角坐标系统为基本数学模型的机器人系统，可以完成在局部空间中任意一点的到达，并遵循可控的运动轨迹。机器臂结构中能够独立运动的关节，称为机器臂的轴，轴的数目称为机器臂的自由度。机器臂的空间几何特点是：轴臂末端可沿着固定线路往返运动，这些线路所在直线或平面之间平行或空间夹角为直角。目前工业用机察臂的自由度一般为3-7.

（1）一种3轴机器臂(如图1)，它的三个轴可以允许机器人沿三个互相垂直的轴的方向进行直线运动，这种机器臂一般被用于简单的搬运工作，例如搬运码头货物的龙门吊和物流仓储立体库房的取货机器人.若该机器臂x，y，z轴长分别为a,b.c. 求：底座固定时机器臂末端手能达到的空间体积.

（2）一种2轴测试用机器臂，结构简化如下(如图2):第一节轴臂视为线段OA,其运动轨迹为以0为圆心，半径为OA的圆；第二节轴臂视为线段AB,其运动轨迹为以A为圆心，半径为AB的圆，且OA⊥AB,两个圆所在平面互相垂真.若两臂长均为1，描述机器臂末端点B能达到的空间区域特征,绘制出图形，并求出区域的面积.

（3）一种3轴测试用机器臂，结构简化如下（如图3）:第一节轴臂视为线段OA,其运动轨迹为以0为球心，半径为OA的球面；第二节轴臂视为线段AB,其运动轨迹为以A为圆心，半径为AB的圆，且始终保持0A⊥AB；第三节轴臂视为线段BC,其运动轨迹为以B为圆心，半径为BC的圆，且始终保持AB⊥BC；若三臂长OA=a，AB=b，BC=c且a,b,c∈，问是否存在数组b，c),使得机器臂末端C能到达以0为球心的单位球体空间任意一点? 若能，例举数组(a，b，c)并证明之；若不能，说明理由。