2022年广东省广州市中考数学试卷（解析版）

这是一份2022年广东省广州市中考数学试卷（解析版），共30页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
2022年广东省广州市中考数学试卷
一、选择题（本大题共10小题，每小题3分，满分30分．在每小题给出的四个选项中，只有一项是符合题目要求的．）
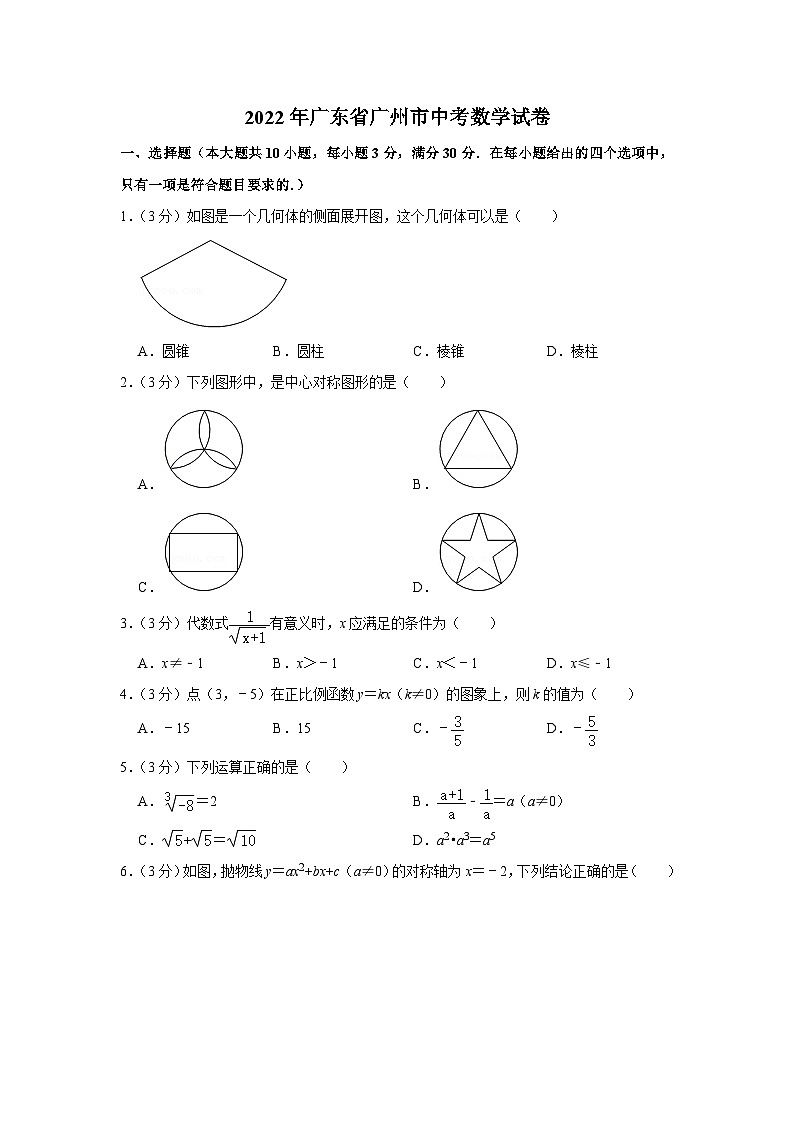
1．（3分）如图是一个几何体的侧面展开图，这个几何体可以是（　　）

A．圆锥 B．圆柱 C．棱锥 D．棱柱
2．（3分）下列图形中，是中心对称图形的是（　　）
A． B．
C． D．
3．（3分）代数式有意义时，x应满足的条件为（　　）
A．x≠﹣1 B．x＞﹣1 C．x＜﹣1 D．x≤﹣1
4．（3分）点（3，﹣5）在正比例函数y＝kx（k≠0）的图象上，则k的值为（　　）
A．﹣15 B．15 C．﹣ D．﹣
5．（3分）下列运算正确的是（　　）
A．＝2 B．﹣＝a（a≠0）
C．+＝ D．a2•a3＝a5
6．（3分）如图，抛物线y＝ax2+bx+c（a≠0）的对称轴为x＝﹣2，下列结论正确的是（　　）

A．a＜0
B．c＞0
C．当x＜﹣2时，y随x的增大而减小
D．当x＞﹣2时，y随x的增大而减小
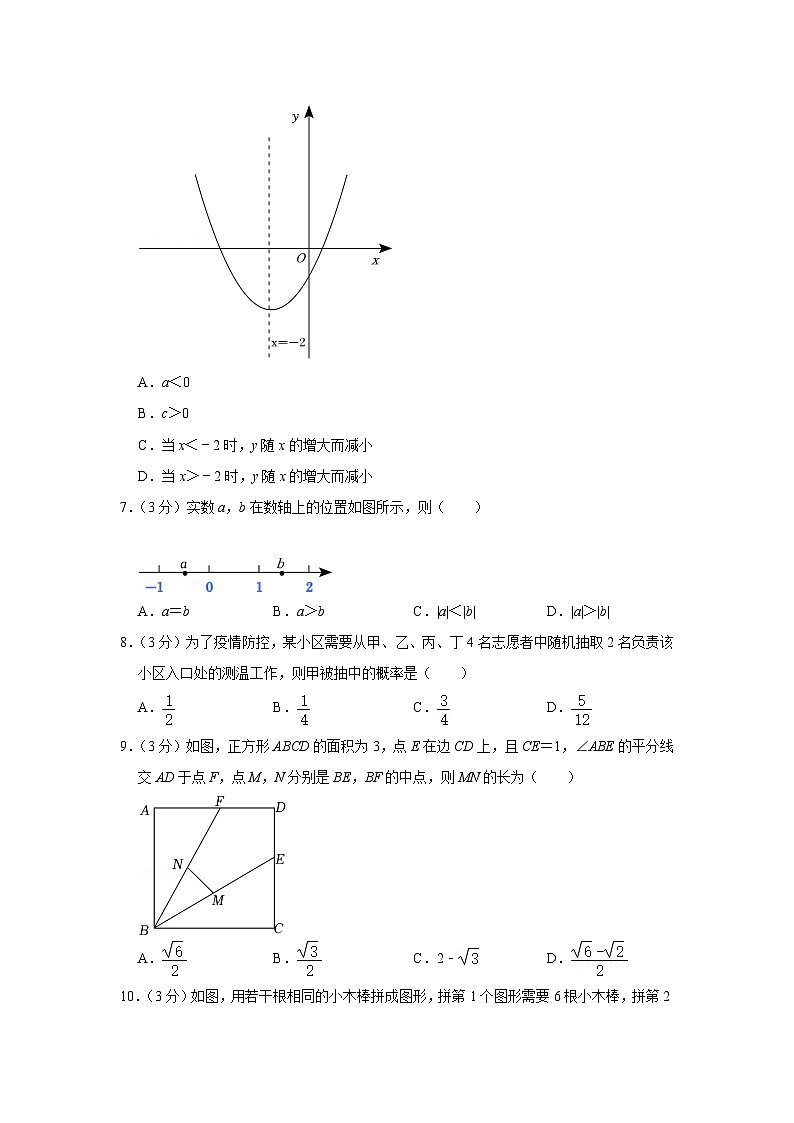
7．（3分）实数a，b在数轴上的位置如图所示，则（　　）


A．a＝b B．a＞b C．|a|＜|b| D．|a|＞|b|
8．（3分）为了疫情防控，某小区需要从甲、乙、丙、丁4名志愿者中随机抽取2名负责该小区入口处的测温工作，则甲被抽中的概率是（　　）
A． B． C． D．
9．（3分）如图，正方形ABCD的面积为3，点E在边CD上，且CE＝1，∠ABE的平分线交AD于点F，点M，N分别是BE，BF的中点，则MN的长为（　　）

A． B． C．2﹣ D．
10．（3分）如图，用若干根相同的小木棒拼成图形，拼第1个图形需要6根小木棒，拼第2个图形需要14根小木棒，拼第3个图形需要22根小木棒……若按照这样的方法拼成的第n个图形需要2022根小木棒，则n的值为（　　）

A．252 B．253 C．336 D．337
二、填空题（本大题共6小题，每小题3分，满分18分。）
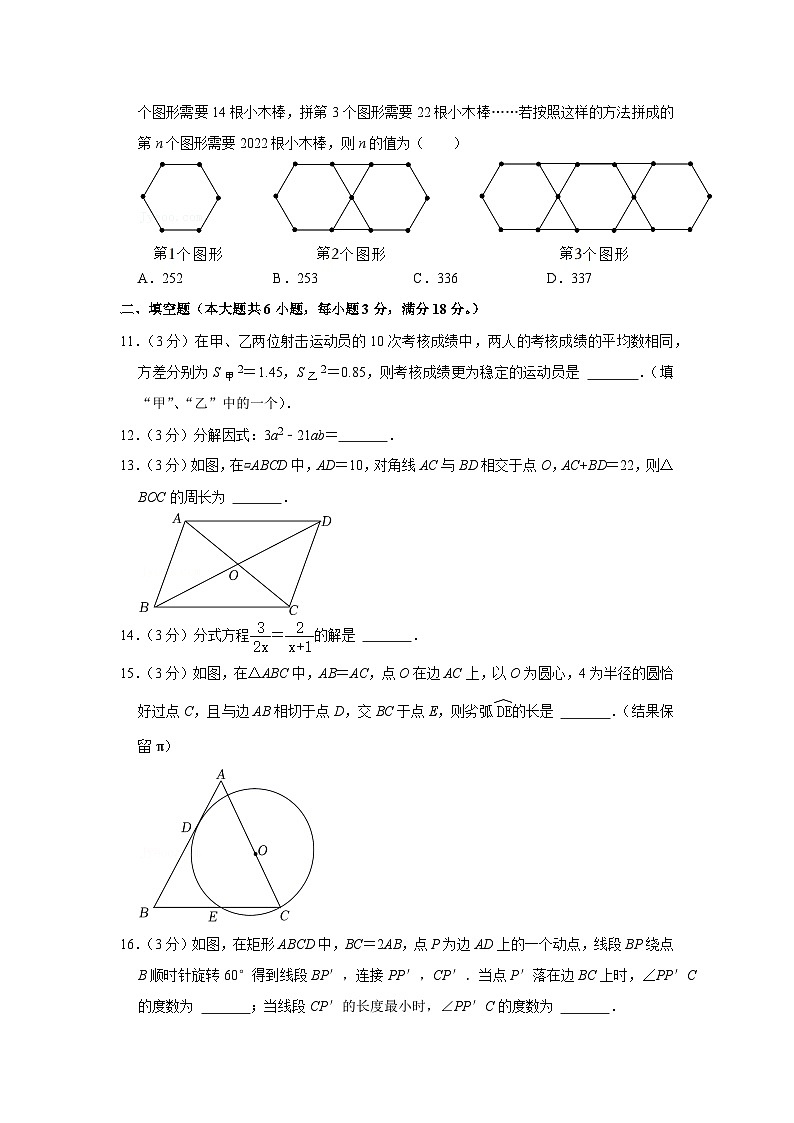
11．（3分）在甲、乙两位射击运动员的10次考核成绩中，两人的考核成绩的平均数相同，方差分别为S甲2＝1.45，S乙2＝0.85，则考核成绩更为稳定的运动员是 　 　．（填“甲”、“乙”中的一个）．
12．（3分）分解因式：3a2﹣21ab＝　 　．
13．（3分）如图，在▱ABCD中，AD＝10，对角线AC与BD相交于点O，AC+BD＝22，则△BOC的周长为 　 　．

14．（3分）分式方程＝的解是 　 　．
15．（3分）如图，在△ABC中，AB＝AC，点O在边AC上，以O为圆心，4为半径的圆恰好过点C，且与边AB相切于点D，交BC于点E，则劣弧的长是 　 　．（结果保留π）

16．（3分）如图，在矩形ABCD中，BC＝2AB，点P为边AD上的一个动点，线段BP绕点B顺时针旋转60°得到线段BP′，连接PP′，CP′．当点P′落在边BC上时，∠PP′C的度数为 　 　；当线段CP′的长度最小时，∠PP′C的度数为 　 　．

三、解答题（本大题共9小题，满分72分．解答应写出文字说明、证明过程或演算步骤．）
17．（4分）解不等式：3x﹣2＜4．
18．（4分）如图，点D，E在△ABC的边BC上，∠B＝∠C，BD＝CE，求证：△ABD≌△ACE．

19．（6分）某校在九年级学生中随机抽取了若干名学生参加“平均每天体育运动时间”的调查，根据调查结果绘制了如下不完整的频数分布表和频数分布直方图．
频数分布表
运动时间t/min
频数
频率
30≤t＜60
4
0.1
60≤t＜90
7
0.175
90≤t＜120
a
0.35
120≤t＜150
9
0.225
150≤t＜180
6
b
合计
n
1
请根据图表中的信息解答下列问题：
（1）频数分布表中的a＝　 　，b＝　 　，n＝　 　；
（2）请补全频数分布直方图；
（3）若该校九年级共有480名学生，试估计该校九年级学生平均每天体育运动时间不低于120min的学生人数．

20．（6分）某燃气公司计划在地下修建一个容积为V（V为定值，单位：m3）的圆柱形天然气储存室，储存室的底面积S（单位：m2）与其深度d（单位：m）是反比例函数关系，它的图象如图所示．
（1）求储存室的容积V的值；
（2）受地形条件限制，储存室的深度d需要满足16≤d≤25，求储存室的底面积S的取值范围．

21．（8分）已知T＝（a+3b）2+（2a+3b）（2a﹣3b）+a2．
（1）化简T；
（2）若关于x的方程x2+2ax﹣ab+1＝0有两个相等的实数根，求T的值．
22．（10分）如图，AB是⊙O的直径，点C在⊙O上，且AC＝8，BC＝6．
（1）尺规作图：过点O作AC的垂线，交劣弧于点D，连接CD（保留作图痕迹，不写作法）；
（2）在（1）所作的图形中，求点O到AC的距离及sin∠ACD的值．

23．（10分）某数学活动小组利用太阳光线下物体的影子和标杆测量旗杆的高度．如图，在某一时刻，旗杆AB的影子为BC，与此同时在C处立一根标杆CD，标杆CD的影子为CE，CD＝1.6m，BC＝5CD．
（1）求BC的长；
（2）从条件①、条件②这两个条件中选择一个作为已知，求旗杆AB的高度．
条件①：CE＝1.0m；条件②：从D处看旗杆顶部A的仰角α为54.46°．
注：如果选择条件①和条件②分别作答，按第一个解答计分．
参考数据：sin54.46°≈0.81，cos54.46°≈0.58，tan54.46°≈1.40．

24．（12分）已知直线l：y＝kx+b经过点（0，7）和点（1，6）．
（1）求直线l的解析式；
（2）若点P（m，n）在直线l上，以P为顶点的抛物线G过点（0，﹣3），且开口向下．
①求m的取值范围；
②设抛物线G与直线l的另一个交点为Q，当点Q向左平移1个单位长度后得到的点Q′也在G上时，求G在≤x≤+1的图象的最高点的坐标．
25．（12分）如图，在菱形ABCD中，∠BAD＝120°，AB＝6，连接BD．
（1）求BD的长；
（2）点E为线段BD上一动点（不与点B，D重合），点F在边AD上，且BE＝DF．
①当CE⊥AB时，求四边形ABEF的面积；
②当四边形ABEF的面积取得最小值时，CE+CF的值是否也最小？如果是，求CE+CF的最小值；如果不是，请说明理由．


2022年广东省广州市中考数学试卷
参考答案与试题解析
一、选择题（本大题共10小题，每小题3分，满分30分．在每小题给出的四个选项中，只有一项是符合题目要求的．）
1．（3分）如图是一个几何体的侧面展开图，这个几何体可以是（　　）

A．圆锥 B．圆柱 C．棱锥 D．棱柱
【分析】根据基本几何体的展开图判断即可．
【解答】解：∵圆锥的侧面展开图是扇形，
∴判断这个几何体是圆锥，
故选：A．
【点评】本题主要考查几何体的展开图，熟练掌握基本几何体的展开图是解题的关键．
2．（3分）下列图形中，是中心对称图形的是（　　）
A． B．
C． D．
【分析】根据中心对称图形的概念进行判断即可．
【解答】解：A．不是中心对称图形，故此选项不合题意；
B．不是中心对称图形，故此选项不合题意；
C．是中心对称图形，故此选项符合题意；
D．不是中心对称图形，故此选项不合题意；
故选：C．
【点评】本题考查的是中心对称图形的概念，中心对称图形是要寻找对称中心，旋转180度后与自身重合．
3．（3分）代数式有意义时，x应满足的条件为（　　）
A．x≠﹣1 B．x＞﹣1 C．x＜﹣1 D．x≤﹣1
【分析】直接利用二次根式有意义的条件、分式有意义的条件分析得出答案．
【解答】解：代数式有意义时，x+1＞0，
解得：x＞﹣1．
故选：B．
【点评】此题主要考查了二次根式有意义的条件以及分式有意义的条件，正确掌握相关定义是解题关键．
4．（3分）点（3，﹣5）在正比例函数y＝kx（k≠0）的图象上，则k的值为（　　）
A．﹣15 B．15 C．﹣ D．﹣
【分析】直接把已知点代入，进而求出k的值．
【解答】解：∵点（3，﹣5）在正比例函数y＝kx（k≠0）的图象上，
∴﹣5＝3k，
解得：k＝﹣，
故选：D．
【点评】此题主要考查了待定系数法求正比例函数解析式，正确得出k的值是解题关键．
5．（3分）下列运算正确的是（　　）
A．＝2 B．﹣＝a（a≠0）
C．+＝ D．a2•a3＝a5
【分析】直接利用立方根的性质以及分式的加减运算法则、二次根式的加减运算法则、同底数幂的乘法运算法则分别判断得出答案．
【解答】解：A．＝﹣2，故此选项不合题意；
B．﹣＝1，故此选项不合题意；
C．+＝2，故此选项不合题意；
D．a2•a3＝a5，故此选项符合题意；
故选：D．
【点评】此题主要考查了立方根的性质以及分式的加减运算、二次根式的加减运算、同底数幂的乘法运算，正确掌握相关运算法则是解题关键．
6．（3分）如图，抛物线y＝ax2+bx+c（a≠0）的对称轴为x＝﹣2，下列结论正确的是（　　）

A．a＜0
B．c＞0
C．当x＜﹣2时，y随x的增大而减小
D．当x＞﹣2时，y随x的增大而减小
【分析】根据图象得出a，c的符号即可判断A、B，利用二次函数的性质即可判断C、D．
【解答】解：∵图象开口向上，
∴a＞0，故A不正确；
∵图象与y轴交于负半轴，
∴c＜0，故B不正确；
∵抛物线开口向上，对称轴为直线x＝﹣2，
∴当x＜﹣2时，y随x的增大而减小，x＞﹣2时，y随x的增大而增大，
故C正确，D不正确；
故选：C．
【点评】此题主要考查了二次函数图象和性质，熟练掌握二次函数的性质是解题关键．
7．（3分）实数a，b在数轴上的位置如图所示，则（　　）


A．a＝b B．a＞b C．|a|＜|b| D．|a|＞|b|
【分析】根据a，b两数的正负以及绝对值大小即可进行判断．
【解答】解：A．∵a＜0，b＞0，∴a≠b，故不符合题意；
B．∵a＜0，b＞0，∴a＜b，故不符合题意；
C．由数轴可知|a|＜|b|，故符合题意；
D．由C可知不符合题意．
故选：C．
【点评】本题主要考查数轴上点的特征以及有理数的大小比较及运算法则，解题的关键在于正确判断a，b的正负，以及绝对值的大小．
8．（3分）为了疫情防控，某小区需要从甲、乙、丙、丁4名志愿者中随机抽取2名负责该小区入口处的测温工作，则甲被抽中的概率是（　　）
A． B． C． D．
【分析】画树状图，共有12种等可能的结果，其中甲被抽中的结果有6种，再由概率公式求解即可．
【解答】解：画树状图如下：

共有12种等可能的结果，其中甲被抽中的结果有6种，
∴甲被抽中的概率为＝，
故选：A．
【点评】本题考查的用树状图法求概率．树状图法可以不重复不遗漏地列出所有可能的结果，适合于两步或两步以上完成的事件．用到的知识点为：概率＝所求情况数与总情况数之比．
9．（3分）如图，正方形ABCD的面积为3，点E在边CD上，且CE＝1，∠ABE的平分线交AD于点F，点M，N分别是BE，BF的中点，则MN的长为（　　）

A． B． C．2﹣ D．
【分析】连接EF，由正方形ABCD的面积为3，CE＝1，可得DE＝﹣1，tan∠EBC＝＝＝，即得∠EBC＝30°，又AF平分∠ABE，可得∠ABF＝∠ABE＝30°，故AF＝＝1，DF＝AD﹣AF＝﹣1，可知EF＝DE＝×（﹣1）＝﹣，而M，N分别是BE，BF的中点，即得MN＝EF＝．
【解答】解：连接EF，如图：

∵正方形ABCD的面积为3，
∴AB＝BC＝CD＝AD＝，
∵CE＝1，
∴DE＝﹣1，tan∠EBC＝＝＝，
∴∠EBC＝30°，
∴∠ABE＝∠ABC﹣∠EBC＝60°，
∵AF平分∠ABE，
∴∠ABF＝∠ABE＝30°，
在Rt△ABF中，AF＝＝1，
∴DF＝AD﹣AF＝﹣1，
∴DE＝DF，△DEF是等腰直角三角形，
∴EF＝DE＝×（﹣1）＝﹣，
∵M，N分别是BE，BF的中点，
∴MN是△BEF的中位线，
∴MN＝EF＝．
故选：D．
【点评】本题考查正方形性质及应用，涉及含30°角的直角三角形三边关系，等腰直角三角形三边关系，解题的关键是根据已知求得∠EBC＝30°．
10．（3分）如图，用若干根相同的小木棒拼成图形，拼第1个图形需要6根小木棒，拼第2个图形需要14根小木棒，拼第3个图形需要22根小木棒……若按照这样的方法拼成的第n个图形需要2022根小木棒，则n的值为（　　）

A．252 B．253 C．336 D．337
【分析】根据图形特征，第1个图形需要6根小木棒，第2个图形需要6×2+2＝14根小木棒，第3个图形需要6×3+2×2＝22根小木棒，按此规律，得出第n个图形需要的小木棒根数即可．
【解答】解：由题意知，第1个图形需要6根小木棒，
第2个图形需要6×2+2＝14根小木棒，
第3个图形需要6×3+2×2＝22根小木棒，
按此规律，第n个图形需要6n+2（n﹣1）＝（8n﹣2）个小木棒，
当8n﹣2＝2022时，
解得n＝253，
故选：B．
【点评】本题主要考查了图形的变化规律，解决问题的关键是由特殊找到规律：第n个图形需要（8n﹣2）个小木棒是解题的关键．
二、填空题（本大题共6小题，每小题3分，满分18分。）
11．（3分）在甲、乙两位射击运动员的10次考核成绩中，两人的考核成绩的平均数相同，方差分别为S甲2＝1.45，S乙2＝0.85，则考核成绩更为稳定的运动员是 　乙　．（填“甲”、“乙”中的一个）．
【分析】首先比较平均数，平均数相同时选择方差较小的即可．
【解答】解：∵两人的考核成绩的平均数相同，方差分别为S甲2＝1.45，S乙2＝0.85，
∴S甲2＞S乙2，
∴考核成绩更为稳定的运动员是乙；
故答案为：乙．
【点评】此题考查了平均数和方差，正确理解方差与平均数的意义是解题的关键．
12．（3分）分解因式：3a2﹣21ab＝　3a（a﹣7b）　．
【分析】直接提取公因式3a，进而分解因式得出答案．
【解答】解：3a2﹣21ab＝3a（a﹣7b）．
故答案为：3a（a﹣7b）．
【点评】此题主要考查了提取公因式法分解因式，正确找出公因式是解题关键．
13．（3分）如图，在▱ABCD中，AD＝10，对角线AC与BD相交于点O，AC+BD＝22，则△BOC的周长为 　21　．

【分析】根据平行四边形对角线互相平分，求出OC+OB的长，即可解决问题．
【解答】解：∵四边形ABCD是平行四边形，
∴AO＝OC＝AC，BO＝OD＝BD，AD＝BC＝10，
∵AC+BD＝22，
∴OC+BO＝11，
∴△BOC的周长＝OC+OB+BC＝11+10＝21．
故答案为：21．
【点评】本题考查平行四边形的性质以及三角形周长等知识，解题的关键是记住平行四边形的对角线互相平分，属于中考基础题．
14．（3分）分式方程＝的解是 　x＝3　．
【分析】按照解分式方程的步骤，进行计算即可解答．
【解答】解：＝，
3（x+1）＝4x，
解得：x＝3，
检验：当x＝3时，2x（x+1）≠0，
∴x＝3是原方程的根，
故答案为：x＝3．
【点评】本题考查了解分式方程，一定要注意解分式方程必须检验．
15．（3分）如图，在△ABC中，AB＝AC，点O在边AC上，以O为圆心，4为半径的圆恰好过点C，且与边AB相切于点D，交BC于点E，则劣弧的长是 　2π　．（结果保留π）

【分析】连接OD，OE，根据等腰三角形的性质和三角形内角和定理可得∠A＝∠COE，再根据切线的性质和平角的定义可得∠DOE＝90°，然后利用弧长公式进行计算即可解答．
【解答】解：连接OD，OE，
∵OC＝OE，
∴∠OCE＝∠OEC，
∵AB＝AC，
∴∠ABC＝∠ACB，
∵∠A+∠ABC+∠ACB＝∠COE+∠OCE+∠OEC，
∴∠A＝∠COE，
∵圆O与边AB相切于点D，
∴∠ADO＝90°，
∴∠A+∠AOD＝90°，
∴∠COE+∠AOD＝90°，
∴∠DOE＝180°﹣（∠COE+∠AOD）＝90°，
∴劣弧的长是＝2π．
故答案为：2π．

【点评】本题考查了切线的性质，弧长的计算，等腰三角形的性质，熟练掌握切线的性质是解题的关键．
16．（3分）如图，在矩形ABCD中，BC＝2AB，点P为边AD上的一个动点，线段BP绕点B顺时针旋转60°得到线段BP′，连接PP′，CP′．当点P′落在边BC上时，∠PP′C的度数为 　120°　；当线段CP′的长度最小时，∠PP′C的度数为 　75°　．

【分析】如图，以AB为边向右作等边△ABE，连接EP′．利用全等三角形的性质证明∠BEP′＝90°，推出点P′在射线EP′上运动，如图1中，设EP′交BC于点O，再证明△BEO是等腰直角三角形，可得结论．
【解答】解：如图，以AB为边向右作等边△ABE，连接EP′．

∵△BPP′是等边三角形，
∴∠ABE＝∠PBP′＝60°，BP＝BP′，BA＝BE，
∴∠ABP＝∠EBP′，
在△ABP和△EBP′中，
，
∴△ABP≌△EBP′（SAS），
∴∠BAP＝BEP′＝90°，
∴点P′在射线EP′上运动，
如图1中，设EP′交BC于点O，

当点P′落在BC上时，点P′与O重合，此时∠PP′C＝180°﹣60°＝120°，
当CP′⊥EP′时，CP′的长最小，此时∠EBO＝∠OCP′＝30°，
∴EO＝﹣OB，OP′＝OC，
∴EP′＝EO+OP′＝OB+OC＝BC，
∵BC＝2AB，
∴EP′＝AB＝EB，
∴∠EBP′＝∠EP′B＝45°，
∴∠BP′C＝45°+90°＝135°，
∴∠PP′C＝∠BP′C﹣∠BP′P＝135°﹣60°＝75°．
故答案为：120°，75°．
【点评】本题考查旋转的性质，矩形的性质，等边三角形的性质，全等三角形的判定和性质，等腰直角三角形的判定和性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，属于中考填空题中的压轴题．
三、解答题（本大题共9小题，满分72分．解答应写出文字说明、证明过程或演算步骤．）
17．（4分）解不等式：3x﹣2＜4．
【分析】移项，合并同类项，系数化为1即可求解．
【解答】解：移项得：3x＜4+2，
合并同类项得：3x＜6，
系数化为1得：x＜2．
【点评】本题考查一元一次不等式的解法，解题关键是熟知不等式的性质以及解一元一次不等式的基本步骤．
18．（4分）如图，点D，E在△ABC的边BC上，∠B＝∠C，BD＝CE，求证：△ABD≌△ACE．

【分析】根据等角对等边可得AB＝AC，然后利用SAS证明△ABD≌△ACE，即可解答．
【解答】证明：∵∠B＝∠C，
∴AB＝AC，
在△ABD和△ACE中，
，
∴△ABD≌△ACE（SAS）．
【点评】本题考查了全等三角形的判定，熟练掌握全等三角形的判定，以及等腰三角形的判定与性质是解题的关键．
19．（6分）某校在九年级学生中随机抽取了若干名学生参加“平均每天体育运动时间”的调查，根据调查结果绘制了如下不完整的频数分布表和频数分布直方图．
频数分布表
运动时间t/min
频数
频率
30≤t＜60
4
0.1
60≤t＜90
7
0.175
90≤t＜120
a
0.35
120≤t＜150
9
0.225
150≤t＜180
6
b
合计
n
1
请根据图表中的信息解答下列问题：
（1）频数分布表中的a＝　14　，b＝　0.15　，n＝　40　；
（2）请补全频数分布直方图；
（3）若该校九年级共有480名学生，试估计该校九年级学生平均每天体育运动时间不低于120min的学生人数．

【分析】（1）根据“频率＝频数÷总数”可得n的值，进而得出a、b的值；
（2）根据a的值即可补全条形统计图；
（3）利用样本估计总体解答即可．
【解答】解：（1）由题意可知，n＝4÷0.1＝40，
∴a＝40×0.35＝14，b＝6÷40＝0.15，
故答案为：14；0.15；40；
（2）补全频数分布直方图如下：

（3）480×＝300（人），
答：估计该校九年级学生平均每天体育运动时间不低于120min的学生人数为300人．
【点评】本题考查频数分布表、频数分布直方图的意义和制作方法，从统计图表中获取数量和数量关系是正确计算的前提，样本估计总体是统计中常用的方法．
20．（6分）某燃气公司计划在地下修建一个容积为V（V为定值，单位：m3）的圆柱形天然气储存室，储存室的底面积S（单位：m2）与其深度d（单位：m）是反比例函数关系，它的图象如图所示．
（1）求储存室的容积V的值；
（2）受地形条件限制，储存室的深度d需要满足16≤d≤25，求储存室的底面积S的取值范围．

【分析】（1）设底面积S与深度d的反比例函数解析式为S＝，把点（20，500）代入解析式求出V的值；
（2）由d的范围和图像的性质求出S的范围．
【解答】解：（1）设底面积S与深度d的反比例函数解析式为S＝，把点（20，500）代入解析式得500＝，
∴V＝10000．
2）由（1）得S＝，
∵S随d的增大而减小，
∴当16≤d≤25时，400≤S≤625，
【点评】此题主要考查反比例函数的性质和概念，解答此题的关键是找出变量之间的函数关系，难易程度适中．
21．（8分）已知T＝（a+3b）2+（2a+3b）（2a﹣3b）+a2．
（1）化简T；
（2）若关于x的方程x2+2ax﹣ab+1＝0有两个相等的实数根，求T的值．
【分析】（1）根据完全平方公式和平方差公式化简T；
（2）根据根的判别式可求a2+ab，再代入计算可求T的值．
【解答】解：（1）T＝（a+3b）2+（2a+3b）（2a﹣3b）+a2
＝a2+6ab+9b2+4a2﹣9b2+a2
＝6a2+6ab；
（2）∵关于x的方程x2+2ax﹣ab+1＝0有两个相等的实数根，
∴Δ＝（2a）2﹣4（﹣ab+1）＝0，
∴a2+ab＝1，
∴T＝6×1＝6．
【点评】本题考查了整式的混合运算，根的判别式，一元二次方程ax2+bx+c＝0（a≠0）的根与Δ＝b2﹣4ac有如下关系：
①当Δ＞0时，方程有两个不相等的实数根；
②当Δ＝0时，方程有两个相等的实数根；
③当Δ＜0时，方程无实数根．
22．（10分）如图，AB是⊙O的直径，点C在⊙O上，且AC＝8，BC＝6．
（1）尺规作图：过点O作AC的垂线，交劣弧于点D，连接CD（保留作图痕迹，不写作法）；
（2）在（1）所作的图形中，求点O到AC的距离及sin∠ACD的值．

【分析】（1）利用尺规作图，作线段AC的垂直平分线即可；
（2）根据垂径定理、勾股定理可求出直径AB＝10，AE＝EC＝3，由三角形中位线定理可求出OE，即点O到AC的距离，在直角三角形CDE中，求出DE，由勾股定理求出CD，再根据锐角三角函数的定义可求出答案．
【解答】解：（1）分别以A、C为圆心，大于AC为半径画弧，在AC的两侧分别相交于P、Q两点，画直线PQ交劣弧于点D，交AC于点E，即作线段AC的垂直平分线即可；
（2）∵AB是⊙O的直径，
∴∠ACB＝90°，
在Rt△ABC中，且AC＝8，BC＝6．
∴AB＝＝10，
∵OD⊥AC，
∴AE＝CE，
又∵OA＝OB，
∴OE是△ABC的中位线，
∴OE＝BC＝4，
即点O到AC的距离为4，
∵DE＝OD﹣CE＝5﹣4＝1，CE＝AC＝3，
∴CD＝＝＝，
∴sin∠ACD＝＝＝．

【点评】本题考查尺规作图，直角三角形的边角关系以及三角形中位线定理，掌握直角三角形的边角关系以及三角形的中位线定理是解决问题的前提．
23．（10分）某数学活动小组利用太阳光线下物体的影子和标杆测量旗杆的高度．如图，在某一时刻，旗杆AB的影子为BC，与此同时在C处立一根标杆CD，标杆CD的影子为CE，CD＝1.6m，BC＝5CD．
（1）求BC的长；
（2）从条件①、条件②这两个条件中选择一个作为已知，求旗杆AB的高度．
条件①：CE＝1.0m；条件②：从D处看旗杆顶部A的仰角α为54.46°．
注：如果选择条件①和条件②分别作答，按第一个解答计分．
参考数据：sin54.46°≈0.81，cos54.46°≈0.58，tan54.46°≈1.40．

【分析】（1）根据已知BC＝5CD，进行计算即可解答；
（2）若选择条件①，根据同一时刻的物高与影长是成比例的，进行计算即可解答；
若选择条件②，过点D作DF⊥AB，垂足为F，根据题意可得DC＝BF＝1.6m，DF＝BC＝8m，然后在Rt△ADF中，利用锐角三角函数的定义求出AF的长，进行计算即可解答．
【解答】解：（1）∵BC＝5CD，CD＝1.6m，
∴BC＝5×1.6＝8（m），
∴BC的长为8m；
（2）若选择条件①：
由题意得：
＝，
∴＝，
∴AB＝12.8，
∴旗杆AB的高度为12.8m；
若选择条件②：

过点D作DF⊥AB，垂足为F，
则DC＝BF＝1.6m，DF＝BC＝8m，
在Rt△ADF中，∠ADF＝54.46°，
∴AF＝DF•tan54.46°≈8×1.4＝11.2（m），
∴AB＝AF+BF＝11.2+1.6＝12.8（m），
∴旗杆AB的高度约为12.8m．

【点评】本题考查了解直角三角形的应用﹣仰角俯角问题，根据题目的已知条件并结合图形添加适当的辅助线是解题的关键．
24．（12分）已知直线l：y＝kx+b经过点（0，7）和点（1，6）．
（1）求直线l的解析式；
（2）若点P（m，n）在直线l上，以P为顶点的抛物线G过点（0，﹣3），且开口向下．
①求m的取值范围；
②设抛物线G与直线l的另一个交点为Q，当点Q向左平移1个单位长度后得到的点Q′也在G上时，求G在≤x≤+1的图象的最高点的坐标．
【分析】（1）用待定系数法求解析式即可；
（2）①设抛物线的解析式为y＝a（x﹣m）2+7﹣m，将点（0，﹣3）代入可得am2+7﹣m＝﹣3，再由a＝＜0，求m的取值即可；
②由题意求出Q点的横坐标为m+，联立方程组，整理得ax2+（1﹣2ma）x+am2﹣m＝0，根据根与系数的关系可得m+m+＝2m﹣，可求a＝﹣2，从而可求m＝2或m＝﹣，确定抛物线的解析式后即可求解．
【解答】解：（1）将点（0，7）和点（1，6）代入y＝kx+b，
∴，
解得，
∴y＝﹣x+7；
（2）①∵点P（m，n）在直线l上，
∴n＝﹣m+7，
设抛物线的解析式为y＝a（x﹣m）2+7﹣m，
∵抛物线经过点（0，﹣3），
∴am2+7﹣m＝﹣3，
∴a＝，
∵抛物线开口向下，
∴a＜0，
∴a＝＜0，
∴m＜10且m≠0；
②∵抛物线的对称轴为直线x＝m，
∴Q点与Q'关于x＝m对称，
∴Q点的横坐标为m+，
联立方程组，
整理得ax2+（1﹣2ma）x+am2﹣m＝0，
∵P点和Q点是直线l与抛物线G的交点，
∴m+m+＝2m﹣，
∴a＝﹣2，
∴y＝﹣2（x+m）2+7﹣m，
∴﹣2m2+7﹣m＝﹣3，
解得m＝2或m＝﹣，
当m＝2时，y＝﹣2（x﹣2）2+5，
此时抛物线的对称轴为直线x＝2，
图象在≤x≤上的最高点坐标为（2，5）；
当m＝﹣时，y＝﹣2（x+）2+，
此时抛物线的对称轴为直线x＝﹣，
图象在﹣2≤x≤﹣1上的最高点坐标为（﹣2，9）；
综上所述：G在≤x≤+1的图象的最高点的坐标为（﹣2，9）或（2，5）．
【点评】本题考查二次函数的图象及性质，熟练掌握二次函数的图象及性质，会用待定系数法求函数的解析式，分类讨论是解题的关键．
25．（12分）如图，在菱形ABCD中，∠BAD＝120°，AB＝6，连接BD．
（1）求BD的长；
（2）点E为线段BD上一动点（不与点B，D重合），点F在边AD上，且BE＝DF．
①当CE⊥AB时，求四边形ABEF的面积；
②当四边形ABEF的面积取得最小值时，CE+CF的值是否也最小？如果是，求CE+CF的最小值；如果不是，请说明理由．

【分析】（1）过点D作DH⊥AB交BA的延长线于H，根据菱形120°内角得邻补角是60°，利用三角函数即可解答；
（2）①设CE⊥AB交AB于M点，过点F作FN⊥AB交BA的延长线于N，因为利用即可求解S四边形ABEF＝S△BEM+S梯形EMNF﹣S△AFN，所以先解直角三角形求出上面求各部分面积需要的边长即可解答；
②设DF＝x，则BE＝DF＝x，过点C作CH⊥AB于点H，过点F作FG⊥CH于点G，过点E作EY⊥CH于点Y，作EM⊥AB于M点，过点F作FN⊥AB交BA的延长线于N，所以四边形EMHY、FNHG是矩形，对边相等，方法同①，用含x的式子表示计算面积需要的各边长并代入到S四边形ABEF＝S△BEM+S梯形EMNF﹣S△AFN中，根号里面化简、合并、配成二次函数的顶点式即可求出最值，从而解答．
【解答】解：（1）过点D作DH⊥AB交BA的延长线于H，如图：

∵四边形ABCD是菱形，
∴AD＝AB＝6，
∴∠BAD＝120°，
∴∠DAH＝60°，
在Rt△ADH中，
DH＝AD•sin∠DAH＝6×＝3，
AH＝AD•cos∠DAH＝6×＝3，
∴BD＝＝＝6；
（2）①设CE⊥AB交AB于M点，过点F作FN⊥AB交BA的延长线于N，如图：

菱形ABCD中，
∵AB＝BC＝CD＝AD＝6，AD∥BC，∠BAD＝120°，
∴∠ABC+∠BAD＝180°，
∴∠ABC＝180°﹣∠BAD＝60°，
在Rt△BCM中，BM＝BC•cos∠ABC＝6×＝3，
∵BD是菱形ABCD的对角线，
∴∠DBA＝ABC＝30°，
在Rt△BEM中，
ME＝BM•tan∠DBM＝3×＝，
BE＝＝＝2，
∵BE＝DF，
∴DF＝2，
∴AF＝AD﹣DF＝4，
在Rt△AFN中，
∠FAN＝180°﹣∠BAD＝60°，
∴FN＝AF•sin∠FAN＝4×＝2，
AN＝AF•cos∠FAN＝4×＝2，
∴MN＝AB+AN﹣BM＝6+2﹣3＝5，
∴S四边形ABEF＝S△BEM+S梯形EMNF﹣S△AFN
＝EM•BM+（EM+FN）•MN﹣AN•FN
＝3+（+2）×5﹣2×2
＝+﹣2
＝7；
②当四边形ABEF的面积取最小值时，CE+CF的值是最小，
理由：设DF＝x，则BE＝DF＝x，过点C作CH⊥AB于点H，过点F作FG⊥CH于点G，
过点E作EY⊥CH于点Y，作EM⊥AB于M点，过点F作FN⊥AB交BA的延长线于N，如图：

∴EY∥FG∥AB，FN∥CH，
∴四边形EMHY、FNHG是矩形，
∴FN＝GH，FG＝NH，EY＝MH，EM＝YH，
由①可知：ME＝BE＝x，
BM＝BE＝x，
AN＝AF＝（AD﹣DF）＝3﹣x，
FN＝AF＝，
CH＝BC＝3，BH＝BC＝3，
∴AM＝AB﹣BM＝6﹣x，
AH＝AB﹣BH＝3，
YH＝ME＝x，
GH＝FN＝，
EY＝MH＝BM﹣BH＝x﹣3，
∴CY＝CH﹣YH＝3﹣x，
FG＝NH＝AN+AH＝6﹣，CG＝CH﹣GH＝3﹣＝x，
∴MN＝AB+AN﹣BM＝6+3﹣x﹣x＝9﹣2x，
∴S四边形ABEF＝S△BEM+S梯形EMNF﹣S△AFN
＝EM•BM+（EM+FN）•MN﹣AN•FN
＝x×x+（x+）•（9﹣2x）﹣（3﹣x）•
＝x2﹣x+9
＝（x﹣3）2+，
∵＞0，
∴当x＝3时，四边形ABEF的面积取得最小值，
CE+CF＝+•
＝+
＝+×
＝+×
＝+，
∵（x﹣3）2≥0，当且仅当x＝3时，（x﹣3）2＝0，
∴CE+CF＝+≥12，
当且仅当x＝3时，CE+CF＝12，即当x＝3时，CE+CF的最小值为12，
∴当四边形ABEF的面积取最小值时，CE+CF的值也最小，最小值为12．
【点评】本题是四边形综合题，考查了菱形性质、解直角三角形、割补法求不规则图形面积、二次函数的顶点式及最值等知识点，也考查了从特殊到一般的数学思想和转化思想，难度较大，计算繁琐，解题关键是熟练掌握二次函数性质，是中考常考题型．
声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布日期：2022/7/18 11:34:44；用户：严兰；邮箱：15527462825；学号：39033143