19.2 菱形 华师版数学八年级下册导学课件

这是一份19.2 菱形 华师版数学八年级下册导学课件，共34页。
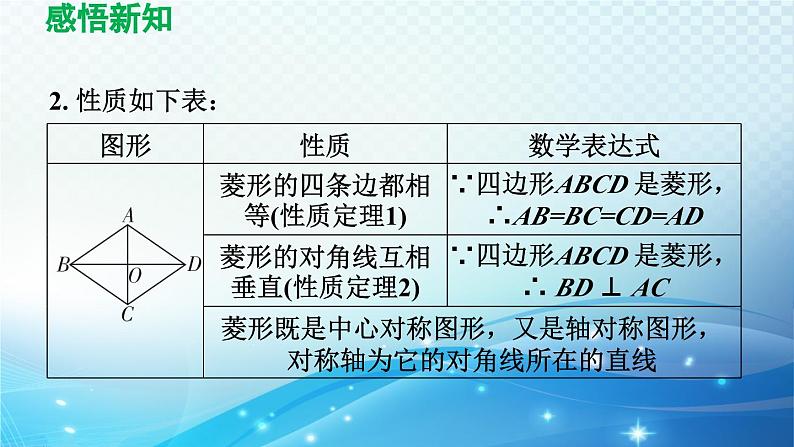
19.2 菱形第19章 矩形、菱形与正方形逐点学练本节小结作业提升学习目标本节要点1学习流程2菱形的定义及其性质菱形的判定知识点感悟新知1菱形的定义及其性质1. 定义：有一组邻边相等的平行四边形叫做菱形.特别提醒●菱形必须满足两个条件：一是平行四边形；二是一组邻边相等.二者必须同时具备，缺一不可.●菱形的定义既是菱形的性质，又是菱形的一种判定方法.感悟新知2. 性质如下表：感悟新知特别提醒：(1)菱形的性质与勾股定理联系，可得对角线与边之间的关系，即边长的平方等于两条对角线长的一半的平方和.(2)如果菱形的一个内角为60°，那么菱形的两条边与较短的对角线构成的三角形为等边三角形.(3)菱形的面积= 底× 高= 两条对角线长的乘积的一半.感悟新知3. 矩形与菱形的区别：(1)矩形和菱形都建立在平行四边形的基础上，矩形是附加一直角，而菱形是附加一组邻边相等；(2)矩形的两条对角线把矩形分割成四个面积相等的等腰三角形，而菱形的两条对角线把菱形分割成四个全等的直角三角形；(3)矩形的对称轴是过两组对边中点的两条直线，而菱形的对称轴是两条对角线所在的直线.感悟新知如图19.2-1，在△ABC中，CD平分∠ACB交AB于点D，DE ∥ AC 交BC 于点E，DF ∥ BC 交AC 于点F. 四边形DECF是菱形吗？为什么？例 1解题秘方：紧扣菱形定义中的“两个条件”进行判断.感悟新知解：四边形DECF 是菱形.理由如下：∵ DE ∥ FC，DF ∥ EC，∴四边形DECF 为平行四边形.∵ AC ∥ DE，∴∠ 2= ∠ 3.∵ CD 平分∠ ACB，∴∠ 1= ∠ 2.∴∠ 1= ∠ 3. ∴ DE=EC.∴平行四边形DECF 为菱形.感悟新知1-1.［中考·鞍山］如图， 在ABCD 中，G 为BC 边上一点，DG=DC，延长DG 交AB 的延长线于点E，过点A 作AF ∥ ED 交CD 的延长线于点F. 求证： 四边形AEDF 是菱形.感悟新知证明：∵四边形ABCD是平行四边形，∴∠BAD＝∠C，AD∥BC，AB∥CD.∵AF∥ED，∴四边形AEDF是平行四边形，∵AD∥BC，∴∠DGC＝∠ADE.∵DG＝DC，∴∠DGC＝∠C，∴∠BAD＝∠ADE，∴AE＝DE，∴平行四边形AEDF是菱形．感悟新知如图19.2-2，在菱形ABCD 中，E，F 分别是BC，CD上的点，且∠ B= ∠ EAF=60°，∠ BAE=18°. 求∠ CEF 的度数.解题秘方：紧扣菱形的性质、三角形外角的性质求解.例2感悟新知解：如图19.2-2，连结AC.∵四边形ABCD 是菱形，∠ B=60°，∴ AB=BC=CD=DA，∠ D= ∠ B=60°.∴△ ABC 和△ ACD 为等边三角形.∴ AB=AC，∠ B= ∠ ACF= ∠ BAC=60°.在菱形中如果出现“30°”“ 60°”“ 120°” “一边等于最短对角线”这些词语时，往往都指向等边三角形，我们需用等边三角形的知识来解决.感悟新知∵∠ EAF=60°，∴∠ BAC= ∠ EAF.∴∠ BAE= ∠ CAF.∴△ ABE ≌△ ACF(A.S.A.).∴ AE=AF.又∵∠ EAF=60°，∴△ EAF 是等边三角形. ∴∠ AEF=60°.∵∠ AEC= ∠ B+ ∠ BAE= ∠ AEF+ ∠ CEF，∴ 60°+18°=60°+ ∠ CEF.∴∠ CEF=18°.感悟新知2-1. 如图， 在菱形ABCD 中， ∠ BAD=80 °，AB 的垂直平分线交对角线AC 于点F，E 为垂足， 连结DF，则∠ CDF 的度数为________.60°感悟新知如图19.2-3，在菱形ABCD 中，对角线AC 与DB 相交于点O. 已知该菱形的周长为8，∠ DAB ∶∠ ABC=1 ∶ 2，求AC，BD 的长.例 3解题秘方：紧扣菱形的边、对角线的性质，在等边三角形和直角三角形中解决问题.感悟新知解：∵四边形ABCD 是菱形，∴ AD ∥ BC，AB=BC=CD=DA，AO=CO，DO=BO.∴∠ DAB+ ∠ ABC=180°.又∵∠ DAB ∶∠ ABC=1 ∶ 2，∴∠ DAB=60°.∵ AB=AD，∴△ ABD 是等边三角形. ∴ BD=AD.感悟新知∵菱形ABCD 的周长为8，∴ AB=BC=CD=AD=2. ∴ BD=2.∴ OD= BD= ×2=1.在Rt △ AOD 中， 由勾股定理， 得感悟新知3-1. ［中考·达州］如图，菱形ABCD 的对角线AC，BD 相交于点O，AC = 24 ， BD = 10 ，则菱形ABCD 的周长为________．52感悟新知3-2. ［中考·乐山］已知菱形ABCD 的两条对角线AC，BD 的长分别是8 cm 和6 cm，则菱形的面积为________cm2．24知识点菱形的判定感悟新知21. 判定定理1：四条边都相等的四边形是菱形.数学语言：如图19.2-4 ①，在四边形ABCD 中，∵ AB=BC=CD=DA，∴四边形ABCD 是菱形.感悟新知2. 判定定理2：对角线互相垂直的平行四边形是菱形.数学语言： 如图19.2-4 ②， 在ABCD 中， ∵ 四边形ABCD 是平行四边形，AC ⊥ BD，∴ ABCD 是菱形.感悟新知注意：(1)判定定理2 必须满足两个条件：一是对角线互相垂直，二是必须是平行四边形，两者缺一不可. 也就是说，利用这一方法判定一个四边形是菱形时，应先证明这个四边形是平行四边形，然后证明它的对角线互相垂直.(2)判定定理2 等价于“对角线互相平分且垂直的四边形是菱形”.感悟新知特别提醒●菱形的判定定理和性质定理是互逆定理.●判定菱形的常见思路：可依据题目特点选取不同的方法.感悟新知[中考·襄阳] 如图19.2-5，BD 为ABCD 的对角线．例4解题秘方：从证四条边相等入手判定菱形.感悟新知(1)作对角线BD的垂直平分线，分别交AD，BC，BD于点E，F，O(尺规作图，不写作法，保留作图痕迹)；解：如图19.2-6，直线EF 即为所求.感悟新知(2)连结BE，DF．求证：四边形BEDF 为菱形．证明：如图19.2-6，∵ EF 垂直平分BD，∴ DO=BO，BE=DE，BF=DF.∵四边形ABCD 是平行四边形，∴ AD ∥ BC，∴∠ DEO= ∠ BFO，∠ EDO= ∠ FBO．∴△ DEO ≌△ BFO．∴ DE=BF，∴ BE=DE=DF=BF，∴四边形BEDF 是菱形．感悟新知4-1. 某四边形的四边长顺次为a，b，c，d， 且a2+b2+c2+d2=ab+bc+cd+ad，则此四边形一定是( )A. 平行四边形B. 矩形C. 菱形D. 正方形C感悟新知如图19.2-7，在 ABCD中，对角线AC，BD相交于点O，过点O 作直线EF ⊥ BD，分别交AD，BC 于点E 和点F，连结BE，DF. 求证：四边形BEDF 是菱形.解题秘方：紧扣对角线垂直这一条件，从判定平行四边形入手判定菱形.例 5感悟新知证明：∵四边形ABCD 是平行四边形，∴ OB=OD，AD ∥ BC.∴∠ EDO= ∠ FBO，∠ OED= ∠ OFB.∴△ OED ≌△ OFB(A.A.S.). ∴ DE=BF.又∵ DE ∥ BF，∴四边形BEDF 是平行四边形.又∵ EF ⊥ BD，∴四边形BEDF 是菱形.感悟新知5-1. 如图， 在三角形纸片ABC 中，AD 是△ ABC 的角平分线，把△ ABC 进行折叠，使点A 与点D 重合，折痕与AB 相交于点E，与AC 相交于点F. 求证：四边形AEDF 是菱形.感悟新知感悟新知又∵点A与点D重合，∴AO＝DO.∴四边形AEDF是平行四边形．又∵AD⊥EF，∴四边形AEDF是菱形．本节小结菱形菱形判定轴对称性定义边的关系角的关系对角线的关系性质边的性质角的性质对角线的性质请完成教材课后习题 作业提升