2022北京师大附中高一（下）期中数学（教师版）

2022北京师大附中高一（下）期中

数    学

班级________  姓名________  学号________

一、选择题（每小题4分，共40分，每题均只有一个正确答案）

1. 若角的终边经过点，则（    ）

A.  B.  C. 2 D.

2. 已知向量，在正方形网格中的位置如图所示，那么向量，的夹角为（    ）

A.  B.  C.  D.

3. 已知，，且，则（    ）

A. 3 B.  C. 5 D. 9

4. 要得到函数的图象，只需把函数的图象（    ）

A. 向左平移个单位 B. 向右移个单位

C. 向左平移个单位 D. 向右平移个单位

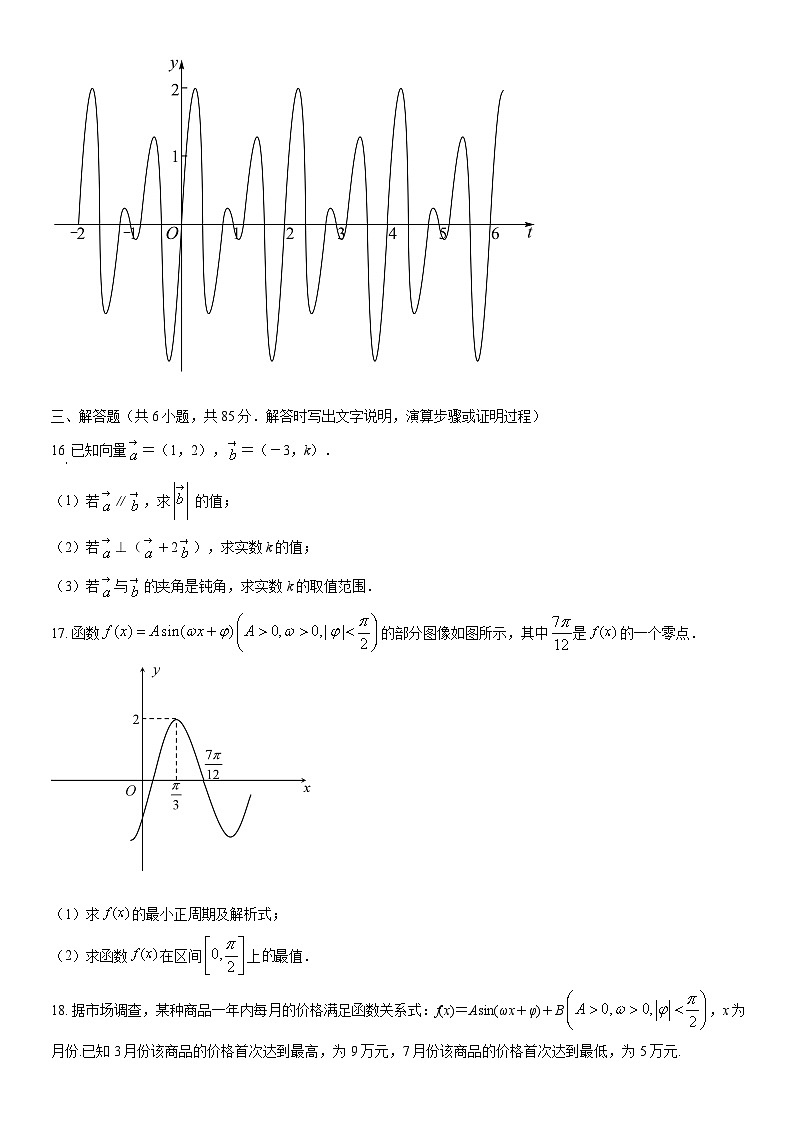
5. 已知，则的值为（    ）

A.  B.  C.  D.

6. “”是“，”的（    ）

A. 充分不必要条件 B. 必要不充分条件

C. 充分必要条件 D. 既不充分也不必要条件

7. 化简的结果为（    ）

A.  B.  C.  D.

8. 在锐角中,设,则的大小关系为

A.  B.  C.  D.

9. 设函数，下列命题中真命题的个数为（    ）

①是奇函数；

②当时，；

③是周期函数；

④在无数个零点；

⑤在上单调递增

A. 1个 B. 2个 C. 3个 D. 4个

10. 在矩形中，，动点在以点为圆心且与相切圆上，则的取值范围为（    ）

A.  B.  C.  D.

二、填空题（每小题5分，共25分）

11. 已知扇形的圆心角为120°，扇形的面积为，则该扇形所在圆的半径为________．

12. 已知，则________．

13. _______.

14. 如图，正方形边长为3，点是线段的靠近点的一个三等分点，若边上存在点，使得成立，则的一个符合题意的值为________．

15. 声音是由物体振动而产生的声波通过介质（空气、固体或液体）传播并能被人的听觉器官所感知的波动现象．在现实生活中经常需要把两个不同的声波进行合成，这种技术被广泛运用在乐器的调音和耳机的主动降噪技术方面．技术人员获取某种声波，其数学模型记为，其部分图象如图所示，对该声波进行逆向分析，发现它是由，两种不同的声波合成得到的，，的数学模型分别记为和，满足．已知，两种声波的数学模型源自于下列四个函数中的两个：①；②；③；④．则，两种声波的数学模型分别是________．（填写序号）

三、解答题（共6小题，共85分．解答时写出文字说明，演算步骤或证明过程）

16 已知向量＝（1，2），＝（－3，k）．

（1）若∥，求 的值；

（2）若⊥（＋2），求实数k的值；

（3）若与夹角是钝角，求实数k的取值范围．

17. 函数的部分图像如图所示，其中是的一个零点．

（1）求的最小正周期及解析式；

（2）求函数在区间上最值．

18. 据市场调查，某种商品一年内每月的价格满足函数关系式：f(x)＝Asin(ωx＋φ)＋B，x为月份.已知3月份该商品的价格首次达到最高，为9万元，7月份该商品的价格首次达到最低，为5万元.

（1）求f(x)的解析式；

（2）求此商品的价格超过8万元的月份.

19. 设函数，．

（1）求的单调递减区间；

（2）若曲线的对称轴只有一条落在区间上，求的取值范围．

20. 已知函数．在下列条件①、条件②、条件③这三个条件中，选择可以确定和值的两个条件作为已知．

（1）求的值；

（2）若函数在区间上是增函数，求实数的最大值．

条件①：最小正周期为；

条件②：最大值与最小值之和为0；

条件③：．

21. 己知集合（且），，且．若对任意，，当时，存在，使得，则称是的元完美子集．

（1）判断下列集合是否是的3元完美子集，并说明理由；

①；                            

②；

（2）若是的3元完美子集，求的最小值；

（3）若是（且）的元完美子集，求证：．

参考答案

1. 若角的终边经过点，则（    ）

A.  B.  C. 2 D.

【答案】D

【解析】

【分析】根据终边上的点坐标求即可.

【详解】由题设，.

故选：D

2. 已知向量，在正方形网格中的位置如图所示，那么向量，的夹角为（    ）

A.  B.  C.  D.

【答案】A

【解析】

【分析】令方格边长为1，、与水平线夹角为，，由结合差角正切公式求夹角大小.

【详解】若每个方格边长为1，、与水平线夹角为，，

由图知：，而，

所以，则 .

故选：A

3. 已知，，且，则（    ）

A. 3 B.  C. 5 D. 9

【答案】B

【解析】

【分析】利用数量积的性质，将所求转化为数量积，然后计算可得.

【详解】因为，，且

所以

所以

故选：B

4. 要得到函数的图象，只需把函数的图象（    ）

A. 向左平移个单位 B. 向右移个单位

C. 向左平移个单位 D. 向右平移个单位

【答案】D

【解析】

【分析】根据图象平移前后解析式判断平移过程.

【详解】由题设，

所以只需把函数的图象向右平移个单位.

故选：D

5. 已知，则的值为（    ）

A.  B.  C.  D.

【答案】C

【解析】

【分析】将齐次式由弦化切，即可求值.

【详解】.

故选：C

6. “”是“，”的（    ）

A. 充分不必要条件 B. 必要不充分条件

C. 充分必要条件 D. 既不充分也不必要条件

【答案】B

【解析】

【分析】取特值可判断充分性，利用诱导公式可判断必要性.

【详解】取，则，

又当，时，

所以“”是“，”的必要不充分条件.

故选：B

7. 化简的结果为（    ）

A.  B.  C.  D.

【答案】D

【解析】

【分析】应用诱导公式化简即可得结果.

【详解】.

故选：D

8. 在锐角中,设,则的大小关系为

A.  B.  C.  D.

【答案】C

【解析】

【详解】试题分析：在锐角中，．

则，所以．故选C．

考点：三角恒等变换

点评：本题应用公式：

9. 设函数，下列命题中真命题的个数为（    ）

①是奇函数；

②当时，；

③是周期函数；

④在无数个零点；

⑤在上单调递增

A. 1个 B. 2个 C. 3个 D. 4个

【答案】C

【解析】

【分析】由奇函数定义验证可判断①；根据x的范围可得的范围，可判断②；考察曲线与曲线系Z，的交点可判断③④；取特值可判断⑤.

【详解】因为，R

所以，是奇函数，①正确；

当时，，所以，所以，②正确；

令，则Z，即Z，

记Z，

由图知，曲线与曲线系Z在区间，，…，内的交点个数逐渐增加且趋于无穷多个，所以原函数不存在周期，故③错误；

如图，曲线与曲线系Z的交点显然有无数个，④正确；

因为，，

且，所以，即，故⑤错误.

故选：C

10. 在矩形中，，动点在以点为圆心且与相切的圆上，则的取值范围为（    ）

A.  B.  C.  D.

【答案】A

【解析】

【分析】先求出圆的半径，由，结合向量数量积运算律将的最大值转化为求的最大值，即可求出结论.

【详解】由题意，设到的距离为，则，

故，

其中，

设的夹角为，，

当且仅当与反向或同向时取得端点值；

综上，的范围为.

故选：A．

二、填空题（每小题5分，共25分）

11. 已知扇形的圆心角为120°，扇形的面积为，则该扇形所在圆的半径为________．

【答案】

【解析】

【分析】令扇形所在圆的半径为，根据扇形的面积公式有，即可求.

【详解】由题意，令扇形所在圆的半径为，则,

∴，故.

故答案为：

12. 已知，则________．

【答案】

【解析】

【分析】把两边平方，利用正弦的二倍角公式即可求解.

【详解】将两边同时平方得

，即，

故答案为：.

13. _______.

【答案】2

【解析】

【分析】由余弦的二倍角公式降幂，同时用诱导公式化，即可求值．

【详解】．

故答案为：2．

【点睛】本题考查余弦的二倍角公式和诱导公式，三角函数求值时一般先化简再求值，变形时有几个方面要注意：一是化同次，二次的降幂为一次，二是同角，利用角的拆分化多角为一角或二角，三是同名，用诱导公式化函数式为同名函数．

14. 如图，正方形的边长为3，点是线段的靠近点的一个三等分点，若边上存在点，使得成立，则的一个符合题意的值为________．

【答案】1（答案不唯一）

【解析】

【分析】取基底（或建立平面直角坐标系），设，用基底表示出，根据x的范围可求得的范围，在范围内的任意实数都可作为答案.

详解】记，

由题知，

又因为

所以

因为，所以，即，

故答案为：1（答案不唯一，在区间内的任意实数都满足.）

15. 声音是由物体振动而产生的声波通过介质（空气、固体或液体）传播并能被人的听觉器官所感知的波动现象．在现实生活中经常需要把两个不同的声波进行合成，这种技术被广泛运用在乐器的调音和耳机的主动降噪技术方面．技术人员获取某种声波，其数学模型记为，其部分图象如图所示，对该声波进行逆向分析，发现它是由，两种不同的声波合成得到的，，的数学模型分别记为和，满足．已知，两种声波的数学模型源自于下列四个函数中的两个：①；②；③；④．则，两种声波的数学模型分别是________．（填写序号）

【答案】②③

【解析】

【分析】由4个函数的周期和的周期之间的关系，结合函数图形取特值排除可得.

【详解】因为的周期，的周期，和的周期

由图知，的周期

所以或

当时，因为

由图知不满足题意，故

故答案为：②③

三、解答题（共6小题，共85分．解答时写出文字说明，演算步骤或证明过程）

16. 已知向量＝（1，2），＝（－3，k）．

（1）若∥，求 的值；

（2）若⊥（＋2），求实数k的值；

（3）若与夹角是钝角，求实数k的取值范围．

【答案】（1）3；   

（2）k＝；   

（3）k＜且k≠－6.

【解析】

【分析】（1）解方程1×k－2×＝0即得解；

（2）解方程1×＋2×＝0即得解；

（3）解不等式1×＋2×k＜0且k≠－6，即得解.

【小问1详解】

解：因为向量＝（1，2），＝（－3，k），且∥，

所以1×k－2×＝0，解得k＝－6，

所以＝＝3．

【小问2详解】

解：因为＋2＝，且⊥，

所以1×＋2×＝0，解得k＝．

【小问3详解】

解：因为与的夹角是钝角，则＜0且与不共线．

即1×＋2×k＜0且k≠－6，所以k＜且k≠－6．

17. 函数的部分图像如图所示，其中是的一个零点．

（1）求的最小正周期及解析式；

（2）求函数在区间上的最值．

【答案】（1）,   

（2）最大值为2，最小值为-1

【解析】

【分析】（1）由图可得A和周期，由周期可得，代最值点坐标可得，然后可得解析式；

（2）由x的范围结合正弦函数性质可得.

【小问1详解】

由图知，，

所以，所以

又因为的图象过点

所以，

所以Z，得Z，

因为，所以

所以

【小问2详解】

因为，

所以

所以

所以，即

所以数在区间上的最大值为2，最小值为-1.

18. 据市场调查，某种商品一年内每月的价格满足函数关系式：f(x)＝Asin(ωx＋φ)＋B，x为月份.已知3月份该商品的价格首次达到最高，为9万元，7月份该商品的价格首次达到最低，为5万元.

（1）求f(x)的解析式；

（2）求此商品的价格超过8万元的月份.

【答案】（1）f(x)＝2sin＋7；（2）2月份、3月份、4月份、10月份、11月份、12月份此商品的价格超过8万元.

【解析】

【分析】（1）由最大值和最小值求得，由周期求得，再用最高点坐标代入可得，从而得解析式；

（2）解不等式2sin＋7>8中在上的整数解即得．

【详解】解（1）由题意可知＝7－3＝4，∴T＝8，

∴ω＝.

又，∴，

即f(x)＝2sin＋7.(*)

又f(x)过点(3，9)，代入(*)式得2sin＋7＝9，

∴sin＝1，∴，k∈Z.

又|φ|<，∴φ＝－，

∴f(x)＝2sin＋7(1≤x≤12，x∈N*).

（2）令f(x)＝2sin＋7>8，

∴sin>，

∴，k∈Z，

可得＋8k<x<＋8k，k∈Z.

又1≤x≤12，x∈N*，∴x＝2，3，4，10，11，12.

即2月份、3月份、4月份、10月份、11月份、12月份此商品的价格超过8万元.

【点睛】本题考查三角函数的应用，解题关键是根据正弦函数的性质确定函数解析式．

19. 设函数，．

（1）求的单调递减区间；

（2）若曲线的对称轴只有一条落在区间上，求的取值范围．

【答案】（1），；   

（2）.

【解析】

【分析】（1）由差角正弦公式、二倍角正余弦公式及辅助角公式可得，再由正弦函数的单调性，应用整体法求单调减区间；

（2）由正弦函数的对称轴方程求得对称轴，，结合已知条件求的范围．

【小问1详解】

由题设，

令，，则，，

所以的单调递减区间为，.

【小问2详解】

令，，则，，

又对称轴只有一条落在上，则.

20. 已知函数．在下列条件①、条件②、条件③这三个条件中，选择可以确定和值的两个条件作为已知．

（1）求的值；

（2）若函数在区间上是增函数，求实数的最大值．

条件①：最小正周期为；

条件②：最大值与最小值之和为0；

条件③：．

【答案】（1）答案见解析；   

（2）.

【解析】

分析】（1）先对函数化简得，根据所选条件并结合正弦函数性质求参数，得到对应解析式，进而求.

（2）由（1）得到的解析式求函数的增区间，再根据题意可求出的最大值

【小问1详解】

选①和②，则且，解得，

所以，则；

选①和③，则，解得，

所以，则；

选②和③，则且，这样的不存在.

综上，选①和②；选①和③；选②和③不存.

【小问2详解】

选①和②：；选①和③：；

均有，得，

所以的增区间为，

因为函数在区间上是增函数，

所以实数的最大值为.

21. 己知集合（且），，且．若对任意，，当时，存在，使得，则称是的元完美子集．

（1）判断下列集合是否是的3元完美子集，并说明理由；

①；                            

②；

（2）若是的3元完美子集，求的最小值；

（3）若是（且）的元完美子集，求证：．

【答案】（1）不是的3元完美子集，是的3元完美子集，理由见解析；   

（2）12；    （3）证明见解析.

【解析】

【分析】（1）根据元完美子集的定义判断可得结论；

（2）不妨设．由，，分别由定义可求得的最小值；

（3）应用反证思想，假设，可知是中个不同的元素，且均属于集合得到矛盾，进而有任意都有，由此可证结论.

【小问1详解】

①因为，又，所以不是的3元完美子集．

②因为，且，而，

所以是的3元完美子集．

【小问2详解】

不妨设．

若，则，，，与3元完美子集矛盾；

若，则，，而，符合题意，此时．

若，则，于是，，则．

综上，的最小值是12．

【小问3详解】

不妨设，存在某个，使得．

所以，

则是中个不同的元素，

且均属于集合，该集合恰有个不同的元素，显然矛盾．

所以对任意，都有．

于是．

即．

等号成立的条件是且．

【点睛】关键点点睛：第三问，应用反证法，首先假设存在某个使得，推得矛盾结论，则有任意都有成立，即可证结论.