2020北京牛栏山一中高一（下）期中数学（教师版）

这是一份2020北京牛栏山一中高一（下）期中数学（教师版），共11页。试卷主要包含了选择题.，填空题.，解答题等内容，欢迎下载使用。
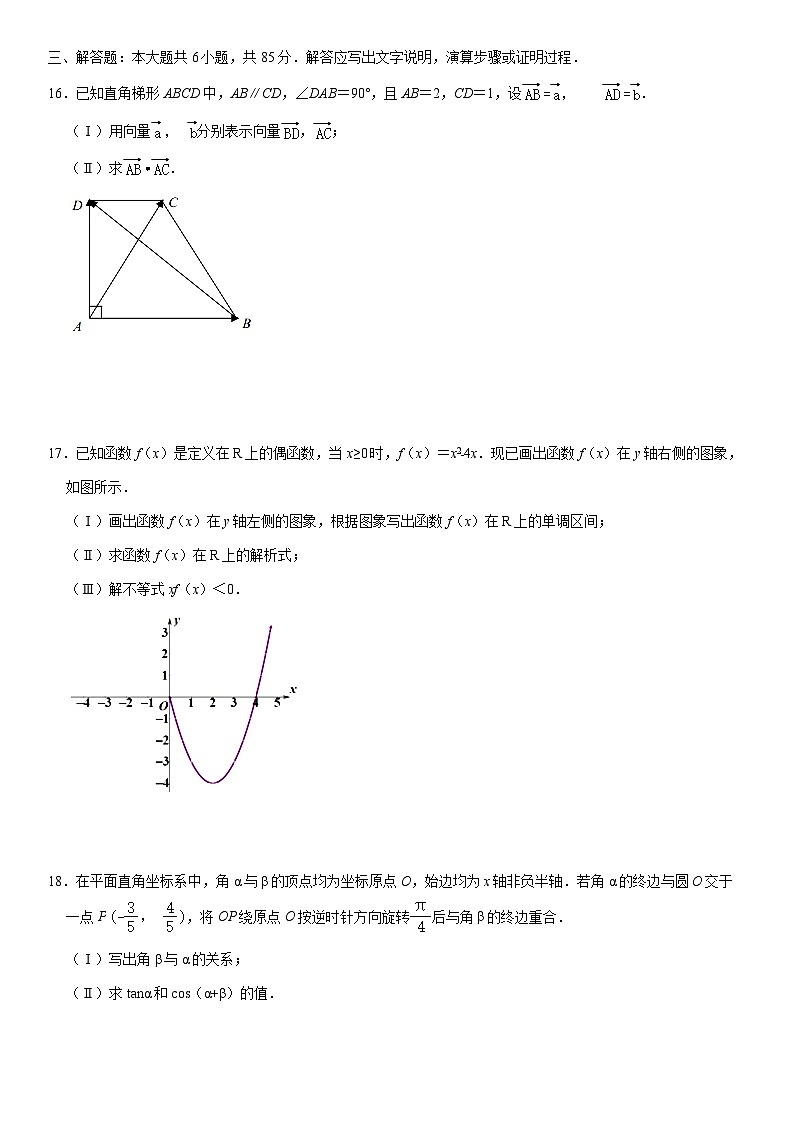
2020北京牛栏山一中高一（下）期中数    学一、选择题（共10小题）.1．已知集合M＝{x||x|＜3}，N＝{1，0，﹣3}，则集合M∩N中元素的个数是（　　）A．1 B．2 C．3 D．42．下列函数中，既是偶函数又在区间（0，+∞）上单调递增的是（　　）A．y＝2x B．y＝﹣x2 C．y＝lg|x| D．y＝cosx3．代数式sin75°cos75°的值为（　　）A． B． C． D．4．+﹣＝（　　）A． B． C． D．5．已知，且，则等于（　　）A．7 B． C．﹣7 D．﹣6．对于非零向量，，下列命题正确的是（　　）A．若，则 B．若，则 C．若，则在上的投影向量为（为与方向相同的单位向量） D．若，则7．已知，，那么＝（　　）A．． B． C． D．8．在四边形ABCD中，“且”是“四边形为正方形”的（　　）A．充分而不必要条件 B．必要而不充分条件 C．充要条件 D．既不充分也不必要条件9．先把函数的图象上所有点的横坐标变为原来的t（t＞0）倍，再向左平移个单位，所得曲线的一部分如图所示，则t，φ的值分别为（　　）A． B． C． D．10．已知函数关于x的方程f（x）＝m，m∈R，有四个不同的实数解x1，x2，x3，x4，则x1+x2+x3+x4的取值范围为（　　）A． B． C． D．（1，+∞）二、填空题（共5小题）.11．已知向量＝（2，1），＝（m，2），若∥，则实数m＝　   　．12．给出下列三个论断：①a＞b；②；③a＜0且b＜0．以其中的两个论断作为条件，余下的一个论断作为结论，写出一个真命题：　   　．13．已知向量，，．若，则λ＝　   　；μ＝　   　．14．在△ABC中，点M是BC的中点，AM＝3，点P在AM上，且满足PM＝2AP，则等于　   　．15．下面有四个命题：①函数y＝cos4x﹣sin4x的最小正周期是π；②函数y＝tan2x的定义域为；③在同一坐标系中，函数y＝sinx的图象和函数y＝x的图象只有一个公共点；④函数y＝cos2x﹣3cosx+2的最小值为．其中，真命题的编号是　   　．（写出所有真命题的编号）
三、解答题：本大题共6小题，共85分．解答应写出文字说明，演算步骤或证明过程．16．已知直角梯形ABCD中，AB∥CD，∠DAB＝90°，且AB＝2，CD＝1，设．（Ⅰ）用向量分别表示向量，；（Ⅱ）求．   17．已知函数f（x）是定义在R上的偶函数，当x≥0时，f（x）＝x2﹣4x．现已画出函数f（x）在y轴右侧的图象，如图所示．（Ⅰ）画出函数f（x）在y轴左侧的图象，根据图象写出函数f（x）在R上的单调区间；（Ⅱ）求函数f（x）在R上的解析式；（Ⅲ）解不等式xf（x）＜0．  18．在平面直角坐标系中，角α与β的顶点均为坐标原点O，始边均为x轴非负半轴．若角α的终边与圆O交于一点P，将OP绕原点O按逆时针方向旋转后与角β的终边重合．（Ⅰ）写出角β与α的关系；（Ⅱ）求tanα和cos（α+β）的值．19．设函数，其中向量，，x∈R，且函数y＝f（x）的图象经过点．（Ⅰ）求实数m的值及函数f（x）的单调增区间；（Ⅱ）当时，求函数f（x）的最大值和最小值；（Ⅲ）求函数f（x）的对称中心的坐标．  20．已知函数．（Ⅰ）求函数f（x）的最小正周期；（Ⅱ）若，求角θ的取值集合；（Ⅲ）设，，且，，求cos（α﹣2β）的值．   21．定义在D上的函数f（x），如果满足：对任意x∈D，存在常数M≥0，都有|f（x）|≤M成立，则称f（x）是D上的有界函数，其中M称为函数f（x）的一个上界．已知函数，g（x）＝1+m•2x+4x．（Ⅰ）当a＝0时，求函数f（x）在区间[，3]上的所有上界构成的集合；（Ⅱ）若函数f（x）为奇函数，求实数a的值；（Ⅲ）若函数g（x）是区间（﹣∞，1]上以2为上界的有界函数，求实数m的取值范围．
参考答案一、选择题：本大题共10小题，每小题4分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项．1．【分析】求出集合M的等价条件，结合集合交集的定义进行求解即可．解：集合M＝{x||x|＜3}＝{x|﹣3＜x＜3}，N＝{0，1，﹣4}，则M∩N＝{0，1}，故选：B．2．【分析】根据题意，依次分析选项中函数的奇偶性与单调性，综合即可得答案．解：根据题意，依次分析选项：对于A，y＝2x，为指数函数，不是偶函数，不符合题意；对于C，y＝lg|x|＝，既是偶函数又在区间（8，+∞）上单调递增，符合题意；故选：C．3．【分析】利用二倍角的正弦化简求值．解：sin75°cos75°＝sin75°cos75°＝．故选：A．4．【分析】根据向量加减的运算性质直接计算即可．解：故选：D．5．【分析】先根据同角三角函数的关系式求得tanα的值，再利用正切的两角和公式即可得解．解：∵，且，∴tanα＝，故选：B．6．【分析】对于A，若＝，则||＝||，＝未必成立；对于B，若•＝•，则•（﹣）＝0，则⊥﹣；对于C，若，则在上的投影向量为±（为与方向相同的单位向量）；对于D，若，则＝0成立．解：对于A，若＝，则||＝||，＝未必成立；故A 错误；对于B，若•＝•，则•（﹣）＝0，则⊥（﹣）；故B错误；对于D，若，则＝0成立．故选：D．7．【分析】直接利用三角函数关系式的变换和半角公式的应用求出结果．解：，sin所以，故＝．故选：D．8．【分析】由“在四边形ABCD中，＝且•＝0”，推出四边形是菱形；菱形未必是正方形，正方形一定是菱形，再根据充分必要条件的定义判断即可．解：由“在四边形ABCD中，＝且•＝0”，推出四边形是菱形；菱形未必是正方形，正方形一定是菱形，故在四边形ABCD中，“且”是“四边形为正方形”的必要不充分条件．故选：B．9．【分析】用ω，φ表示出函数解析式，根据函数周期计算ω，根据图象上的特殊点计算φ．解：由题意可知变换后的函数解析式为f（x）＝sin[（x+）+φ]＝sin（++φ），由函数图象可知f（x）的周期为T＝4（﹣）＝π，∴＝2，即t＝．由图象可知f（）＝﹣1，即sin（++φ）＝﹣1，又|φ|＜，∴φ＝﹣．故选：D．10．【分析】作出函数图象，根据二次函数的对称性及对数函数，绝对值函数的性质，可得x1+x2＝﹣2，x3x4＝1，，转化后构造新函数直接求解即可．解：作出函数图象如图所示，设x1＜x2＜x3＜x4，由二次函数的对称性可知，即x1+x2＝﹣2，∴，设，又，g（5）＝0，故选：C．二、填空题：本大题共5小题，每小题5分，共25分．11．【分析】根据题意，由向量平行的坐标表示方法可得若∥，则有1×m＝2×2，解可得m的值，即可得答案．解：根据题意，向量＝（2，1），＝（m，2），若∥，则有1×m＝2×2，即m＝5；故答案为：412．【分析】根据不等式的关系，结合命题关系进行判断即可．解：若①a＞b；③a＜0且b＜0，则0＞a＞b，则②成立，若；a＜0且b＜0，则a＞b成立，故答案为：若a＞b，a＜0且b＜2，则，或者若，a＜0且b＜7，则a＞b．13．【分析】根据平面向量的坐标运算列方程计算．解：由题意可知，解得：λ＝1，μ＝2．故答案为：4，2．14．【分析】利用向量运算的几何意义，可知，代入原式，根据已知条件容易求解．解：因为M是BC的中点，故，所以＝，故＝2，＝1．＝2×1×4×（﹣1）＝﹣4．故答案为：﹣4．15．【分析】①将三角函数进行化简，利用周期公式求函数的周期．②利用正切函数定义求解判断．③利用函数的平移关系求函数的解析式．④利用配方法求三角函数的最值判断．解：①因为y＝cos4x﹣sin4x＝（sin2x+cos2x）（cos2x﹣sin2x）＝cos2x，所以函数的周期T＝＝π，所以①正确．②对于函数y＝tan2x，2x≠+kπ，k∈Z；∴x≠+，k∈Z；所以②错误．③设f（x）＝sinx﹣x，则f'（x）＝cosx﹣1≤0，函数f（x）单调递减，∵f（0）＝0，∴方程f（x）＝0只有一个解，即函数y＝sinx的图象和函数y＝x的图象只有一个公共点，所以③正确．④因为y＝cos5x﹣3cosx+2＝（cosx﹣）2﹣，﹣1≤cosx≤1，所以cosx＝1时，y的最小值为0，所以④错误．故答案为：①③．三、解答题：本大题共6小题，共85分．解答应写出文字说明，演算步骤或证明过程．16．【分析】（Ⅰ）根据向量加法、减法的几何意义计算即可；（Ⅱ）将分别用基底向量表示出来，计算即可．解：（Ⅰ）由已知：＝，所以：，＝．所以．所以＝＝＝．17．【分析】（I）结合已知及偶函数的图象关于y轴对称性质可求；（II）由已知函数解析式及偶函数的定义可求；（III）结合函数的图象即可直接求解．解：（I）根据偶函数的图象关于y轴对称可得图象如图所示；结合图象可得函数f（x）的单调增区间[﹣2，0]，（2，+∞），减区间（﹣∞，﹣2），（0，5）；根据偶函数的对称性可知，当x＜0时f（x）＝x2+2x，（III）由xf（x）＜0可得或，故不等式的解集为{x|0＜x＜4或x＜﹣4}．18．【分析】（Ⅰ）根据任意角的定义即可得解；（Ⅱ）由三角函数的定义可求得tanα，cosα和sinα的值；再根据二倍角公式可得cos2α和sin2α的值；而cos（α+β）＝cos（2α+），利用余弦的两角和公式展开后，代入相关数据进行运算即可．解：（Ⅰ）β＝α+．（Ⅱ）∵P，∴cos2α＝2cos2α﹣1＝2×﹣5＝，sin2α＝2sinαcosα＝2×（）×＝．∴cos（α+β）＝cos（2α+）＝cos2α•cos﹣sin2α•sin＝×﹣（）×＝．19．【分析】先化简出f（x），利用函数图象经过点（）求出m的值．（Ⅰ）根据函数y＝sinx的单调性求出f（x）的单调区间；（Ⅱ）利用换元思想研究f（x）的最值；（Ⅲ）令函数f（x）＝0，求出f（x）的对称中心的坐标．解：由已知得f（x）＝＝sin2x+mcos2x+m．（Ⅰ）因为f（）＝2，即，得m＝1．令，解得，（Ⅱ）因为，所以，所以，，（Ⅲ）令，解得：，即，k∈Z．故对称中心的坐标为，k∈Z．20．【分析】结合诱导公式、二倍角公式和辅助角公式将函数f（x）化简为f（x）＝sin（2x﹣）．（Ⅰ）利用T＝得解；（Ⅱ）f（θ）＝sin（2θ﹣）＝，再结合正弦函数的图象与性质即可得解；（Ⅲ）由和，可求得sin（α+）和cos（α+）的值；由和，可求得sin（2β﹣）和cos（2β﹣）的值；而cos（α﹣2β）＝﹣cos[（α+）﹣（2β﹣）]，利用余弦的两角差公式展开后，代入相关数据进行运算即可．解：＝sin（x﹣+）sin（x﹣）+sinxcosx＝sin[2（x﹣）]+sinxcosx＝sin（2x﹣）．（Ⅱ）f（θ）＝sin（2θ﹣）＝，∴θ＝+kπ或+kπ，k∈Z，（Ⅲ）∵，∵，∴α+∈（，），∵，∵，∴2β﹣∈（，），∴cos（α﹣2β）＝﹣cos[（α+）﹣（2β﹣）]＝﹣×﹣×＝．21．【分析】（Ⅰ）函数f（x）定义域为（1，+∞），令h（x）＝，分析单调性，求出函数h（x）在[，3]上值域，再求出f（x）在[，3]上值域，根据有界函数的定义即可得出答案．（Ⅱ）根据奇函数定义，可得f（﹣x）＝﹣f（x），列式log2＝log2，进而解出a的值．（Ⅲ）根据有界函数的定义可得，|g（x）|≤2在区间（﹣∞，1]上恒成立，即﹣3（）x﹣2x≤m≤（）x﹣2x，在区间（﹣∞，1]上恒成立，只需[﹣3（）x﹣2x]max≤m且m≤[（）x﹣2x]min，即可得出答案．解：（Ⅰ）函数f（x）＝log2定义域为（4，+∞），令h（x）＝在（1，+∞）单调递减，所以f（x）在[，3]上值域为[﹣1，3]，所以函数f（x）在区间[，3]上的所有上界构成的集合为[3，+∞）．则f（﹣x）＝﹣f（x），而当a＝1时不合题意，故a＝1．则|g（x）|≤2在区间（﹣∞，5]上恒成立，所以﹣2≤1+m•2x+4x≤4，在区间（﹣∞，1]上恒成立，即﹣3（）x﹣2x≤m≤（）x﹣2x，在区间（﹣∞，1]上恒成立，设2x＝t，q（t）＝﹣﹣t，p（t）＝﹣t，q′（t）＝，令q′（t）＝0得t＝，在（，2）上，q′（t）＜0，q（t）单调递减，又因为p（t）在（3，2）上单调递减，所以m的取值范围为[﹣2，﹣]．