2022-2023学年辽宁省鞍山市高新实验学校七年级（下）第一次质检数学试卷（含解析）

这是一份2022-2023学年辽宁省鞍山市高新实验学校七年级（下）第一次质检数学试卷（含解析），共21页。试卷主要包含了选择题，解答题等内容，欢迎下载使用。
2022-2023学年辽宁省鞍山市高新实验学校七年级（下）第一次质检数学试卷
一、选择题（每小题2分，共16分）
1．在实数：3.14159，，1.010010001，4.21，π，中，无理数有（　　）
A．1个 B．2个 C．3个 D．4个
2．如图，直线a、b被直线c所截，下列说法不正确的是（　　）

A．∠1和∠4是内错角 B．∠2和∠3是同旁内角
C．∠1和∠3是同位角 D．∠3和∠4互为邻补角
3．如图，AB∥CD，∠1＝62°，FG平分∠EFD，则∠FGB的度数等于（　　）

A．122° B．151° C．149° D．97°
4．估计的值在（　　）
A．2到3之间 B．3到4之间 C．4到5之间 D．5到6之间
5．若+（5﹣y）2＝0，则x+y的平方根是（　　）
A．9 B．±3 C．3 D．±9
6．如图，已知AE∥BD，∠1＝120°，∠2＝30°，则∠C的度数是（　　）

A．20° B．22° C．25° D．30°
7．下列结论正确有（　　）
①过一点有且只有一条直线与已知直线平行；
②垂直于同一条直线的两条直线互相平行；
③同位角相等，两直线平行；
④在同一平面内，过一点有且只有一条直线与已知直线垂直；
⑤两条平行线被第三条直线所截，同位角的角平分线互相平行．
A．1个 B．2个 C．3个 D．4个
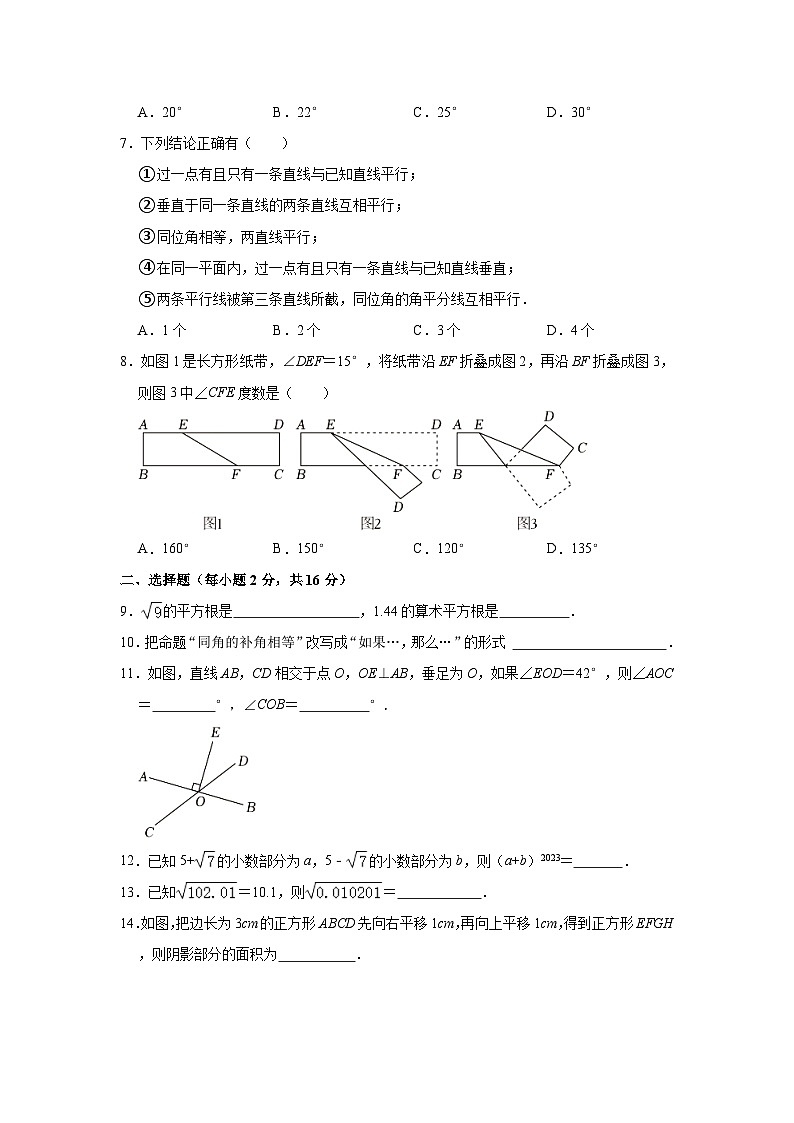
8．如图1是长方形纸带，∠DEF＝15°，将纸带沿EF折叠成图2，再沿BF折叠成图3，则图3中∠CFE度数是（　　）

A．160° B．150° C．120° D．135°
二、选择题（每小题2分，共16分）
9．的平方根是　 　，1.44的算术平方根是　 　．
10．把命题“同角的补角相等”改写成“如果…，那么…”的形式 　 　．
11．如图，直线AB，CD相交于点O，OE⊥AB，垂足为O，如果∠EOD＝42°，则∠AOC＝　 　°，∠COB＝　 　°．

12．已知5+的小数部分为a，5﹣的小数部分为b，则（a+b）2023＝　 　．
13．已知＝10.1，则＝　 　．
14．如图，把边长为3cm的正方形ABCD先向右平移1cm，再向上平移1cm，得到正方形EFGH，则阴影部分的面积为　 　．

15．若∠A与∠B的一组边互相平行，另一组边互相垂直，且∠A等于62°，则∠B的度数为 　 　．
16．将一副直角三角板ABC，ADE按如图1所示位置摆放，其中∠ACB＝∠AED＝90°，∠ADE＝∠DAE＝45°，∠BAC＝30°，∠ABC＝60°．若将三角板ADE绕点A按每秒3°的速度顺时针旋转180°，如图2，在此过程中，设旋转时间为t秒，当线段DE与三角板ABC的一条边平行时，t＝　 　．

三、解答题（68分）
17．如图，在由边长为1个单位长度的小正方形组成的网格中，给出了格点△ABC（顶点为网格线的交点）．
（1）将△ABC先向左平移5个单位，再向下平移3个单位，得到△A1B1C1，并画出平移后的△A1B1C1；
（2）△ABC的面积为 　 　．

18．（1）+﹣
（2）3﹣||
19．解方程：
（1）9（x﹣1）2﹣4＝21；
（2）27（2x﹣1）3＝﹣125．
20．已知∠1＝∠2，∠3＝∠4，∠5＝∠A，试说明：BE∥CF．
请完善下面解答过程，并填写理由．
解：∵∠3＝∠4（已知），
∴AE∥　 　（ 　 　），
∴∠EDC＝　 　（两直线平行，内错角相等），
∵∠5＝∠A（已知），
∴∠EDC＝　 　（ 　 　），
∴DC∥AB（同位角相等，两直线平行），
∴∠5+∠ABC＝180°（ 　 　），
即∠5+∠2+∠3＝180°，
∵∠1＝∠2（已知），
∴∠5+∠1+∠3＝180°（等量代换），
即∠BCF+∠3＝180°，
∴BE∥　 　（ 　 　）．

21．已知2a+1的算术平方根是5，a+b﹣2的立方根是2，求a+b的平方根．
22．如图，直线AB、CD相交于点O，OE⊥OF，∠BOF＝∠BOE+20°，OC平分∠AOE，求∠DOE的度数．

23．如图，已知点E、F在直线AB上，点G在线段CD上，ED与FG交于点H，∠C＝∠EFG，∠CED＝∠GHD．
（1）求证：AB∥CD；
（2）若∠EHF＝75°，∠D＝35°，求∠AEM的度数．

24．已知：AB∥CD，直线EF交AB于点E，交CD于点F，点G在CD上，点P在直线EF右侧，且在直线AB和CD之间，连接PE、PG．
（1）如图1，连接EG，若EG平分∠PEF，∠BEP+∠PGE＝110°，∠PGD＝∠EFD，∠PGD＝30°，求∠BEP的度数；
（2）如图2，若EF平分∠PEA，∠PGD的平分线GN所在的直线与EF相交于点H，则∠EPG与∠EHG之间的数量关系是什么，并说明理由．



参考答案
一、选择题（每小题2分，共16分）
1．在实数：3.14159，，1.010010001，4.21，π，中，无理数有（　　）
A．1个 B．2个 C．3个 D．4个
【分析】根据无理数的定义，可得答案．
解：π是无理数，
故选：A．
【点评】此题主要考查了无理数的定义，注意带根号的要开不尽方才是无理数，无限不循环小数为无理数．如π，，0.8080080008…（每两个8之间依次多1个0）等形式．
2．如图，直线a、b被直线c所截，下列说法不正确的是（　　）

A．∠1和∠4是内错角 B．∠2和∠3是同旁内角
C．∠1和∠3是同位角 D．∠3和∠4互为邻补角
【分析】根据同位角，对顶角，同旁内角以及余角的定义作出判断．
解：A、∠1与∠4不是同位角、内错角、同旁内角，故本选项符合题意．
B、∠2和∠3是同旁内角，故本选项不符合题意．
C、∠1和∠3是同位角，故本选项不符合题意．
D、∠3和∠4互为邻补角，故本选项不符合题意．
故选：A．
【点评】考查了同位角、内错角、同旁内角以及对顶角等，解答此类题确定三线八角是关键，可直接从截线入手．对平面几何中概念的理解，一定要紧扣概念中的关键词语，要做到对它们正确理解，对不同的几何语言的表达要注意理解它们所包含的意义．
3．如图，AB∥CD，∠1＝62°，FG平分∠EFD，则∠FGB的度数等于（　　）

A．122° B．151° C．149° D．97°
【分析】根据平行线的性质及角平分线定义求出∠GFD＝31°，再根据平行线的性质求解即可．
解：∵AB∥CD，∠1＝62°，
∴∠EFD＝∠1＝62°，
∵FG平分∠EFD，
∴∠GFD＝∠EFD＝31°，
∵AB∥CD，
∴∠FGB+∠GFB＝180°，
∴∠FGB＝149°，
故选：C．
【点评】此题考查了平行线的性质，熟记“两直线平行，同位角相等”、“两直线平行，同旁内角互补”是解题的关键．
4．估计的值在（　　）
A．2到3之间 B．3到4之间 C．4到5之间 D．5到6之间
【分析】直接利用估算无理数的方法得出的取值范围进而得出答案．
解：∵9＜15＜16，
∴3＜＜4，
∴4＜＜5，
故选：C．
【点评】此题主要考查了估算无理数的大小，正确得出的取值范围是解题关键．
5．若+（5﹣y）2＝0，则x+y的平方根是（　　）
A．9 B．±3 C．3 D．±9
【分析】根据非负数的性质列式求解，即可得到x、y的值，然后利用平方根的定义解答．
解：∵+（5﹣y）2＝0，而≥0，（5﹣y）2≥0，
∴x﹣4＝0，5﹣y＝0，
解得x＝4，y＝5，
故x+y＝4+5＝9，9的平方根是±3．
故选：B．
【点评】本题考查了算术平方根非负数，平方数非负数的性质，根据几个非负数的和等于0，则每一个算式都等于0列式是解题的关键．
6．如图，已知AE∥BD，∠1＝120°，∠2＝30°，则∠C的度数是（　　）

A．20° B．22° C．25° D．30°
【分析】首先根据平行线的性质得∠CBD＝∠1＝120°，再根据对顶角相等得∠CDB＝∠2＝30°，然后利用三角形的内角和定理可求出∠C的度数．
解：∵AE∥BD，∠1＝120°，
∴∠CBD＝∠1＝120°，
∴∠CDB＝∠2＝30°，
∵∠C+∠CBD+∠CDB180°，
即∠C+120°+30°＝180°，
∴∠C＝30°，
故选：D．
【点评】此题主要考查了平行线的性质，对顶角的性质，三角形的内角和定理，解答此题的关键是熟练掌握平行线的性质，难点是应用转化思想，将∠1，∠2转化到△BCD中．
7．下列结论正确有（　　）
①过一点有且只有一条直线与已知直线平行；
②垂直于同一条直线的两条直线互相平行；
③同位角相等，两直线平行；
④在同一平面内，过一点有且只有一条直线与已知直线垂直；
⑤两条平行线被第三条直线所截，同位角的角平分线互相平行．
A．1个 B．2个 C．3个 D．4个
【分析】根据平行线的判定和性质、垂线的性质、平行公理进行判断即可．
解：①过直线外一点有且只有一条直线与已知直线平行；故不符合题意；
②在同一平面内，垂直于同一条直线的两条直线互相平行；故不符合题意；
③同位角相等，两直线平行；故符合题意；
④在同一平面内，过一点有且只有一条直线与已知直线垂直；故符合题意；
⑤两条平行线被第三条直线所截，同位角的角平分线互相平行．故符合题意；
故选：C．
【点评】本题考查了平行线的判定和性质，垂线的性质、平行公理，熟练掌握平行线的判定和性质是解题的关键．
8．如图1是长方形纸带，∠DEF＝15°，将纸带沿EF折叠成图2，再沿BF折叠成图3，则图3中∠CFE度数是（　　）

A．160° B．150° C．120° D．135°
【分析】由矩形的性质可知AD∥BC，由此可得出∠BFE＝∠DEF＝10°，再根据翻折的性质可知每翻折一次减少一个∠BFE的度数，由此即可算出∠CFE度数．
解：∵四边形ABCD为长方形，
∴AD∥BC，
∴∠BFE＝∠DEF＝15°．
由翻折的性质可知：图2中，∠EFC＝180°﹣∠BFE＝165°，∠BFC＝∠EFC﹣∠BFE＝150°，
∴图3中，∠CFE＝∠BFC﹣∠BFE＝135°．
故选：D．
【点评】本题考查了翻折变换以及矩形的性质，解题的关键是找出∠CFE＝180°﹣3∠BFE．本题属于基础题，难度不大，解决该题型题目时，根据翻折变换找出相等的边角关系是关键．
二、选择题（每小题2分，共16分）
9．的平方根是　　，1.44的算术平方根是　1.2　．
【分析】根据平方根的定义和算术平方根的定义解答即可得．
解：∵＝3，
∴的平方根是±，
1.44的算术平方根是1.2，
故答案为：±，1.2．
【点评】本题主要考查平方根和算术平方根，熟练掌握平方根的定义和算术平方根的定义是解题的关键．
10．把命题“同角的补角相等”改写成“如果…，那么…”的形式 　如果两个角是同一个角的补角，那么这两个角相等　．
【分析】“同角的补角相等”的条件是：两个角是同一个角的补角，结论是：这两个角相等．据此即可写成所要求的形式．
解：“同角的补角相等”的条件是：两个角是同一个角的补角，结论是：这两个角相等．
则将命题“同角的补角相等”改写成“如果…那么…”形式为：如果两个角是同一个角的补角，那么这两个角相等．
故答案是：如果两个角是同一个角的补角，那么这两个角相等．
【点评】本题考查了命题的叙述，正确分清命题的条件和结论是把命题写成“如果…那么…”的形式的关键．
11．如图，直线AB，CD相交于点O，OE⊥AB，垂足为O，如果∠EOD＝42°，则∠AOC＝　48　°，∠COB＝　132　°．

【分析】先根据垂直的定义求出∠BOE＝90°，然后求出∠BOD的度数，再根据对顶角相等求出∠AOC的度数，再根据邻补角的定义求出∠COB的度数．
解：∵OE⊥AB，
∴∠BOE＝90°，
∵∠EOD＝42°，
∴∠BOD＝∠BOE﹣∠EOD＝90°﹣42°＝48°，
∴∠AOC＝∠BOD＝48°（对顶角相等），
∠COB＝180°﹣∠BOD＝180°﹣48°＝132°．
故答案为：48，132．
【点评】本题考查了垂线的定义，对顶角相等，邻补角的和等于180°，要注意领会由垂直得直角这一要点．
12．已知5+的小数部分为a，5﹣的小数部分为b，则（a+b）2023＝　1　．
【分析】先求出的范围，推出7＜5+＜8和2＜5﹣＜3，求出a、b的值，再代入求出即可．
解：∵2＜＜3，
∴7＜5+＜8，
∴a＝5+﹣7＝﹣2，
∵2＜＜3
∴﹣3＜﹣＜﹣2，
∴2＜5﹣＜3，
∴b＝5﹣﹣2＝3﹣，
∴（a+b）2023＝（﹣2+3﹣）2023＝12023＝1．
故答案为：1．
【点评】本题考查了估算无理数的大小，解题的关键是得出7＜5+＜8和2＜5﹣＜3，题目比较好，但是一道比较容易出错的题目．
13．已知＝10.1，则＝　0.101　．
【分析】举特殊例子总结规律后即可得出答案．
解：∵＝100，＝10，＝1，＝0.1，＝0.01，
∴被开方数的小数点每向左移动两位，那么其算术平方根就向左移动一位，
∵＝10.1，0.010201是102.01将小数点向左移动四位而得，
∴＝0.101．
故答案为：0.101．
【点评】本题主要考查算术平方根，列举特殊数值总结规律是解题的关键．
14．如图，把边长为3cm的正方形ABCD先向右平移1cm，再向上平移1cm，得到正方形EFGH，则阴影部分的面积为　4cm2　．

【分析】根据平移的性质判断出阴影部分是正方形并求出边长，然后根据面积公式列式进行计算即可得解．
解：∵正方形ABCD向右平移1cm，向上平移1cm，
∴阴影部分是边长为3﹣1＝2cm的正方形，
∴阴影部分的面积＝22＝4cm2．
故答案为：4cm2．
【点评】本题考查了平移的性质，判断出阴影部分是正方形并求出边长是解题的关键．
15．若∠A与∠B的一组边互相平行，另一组边互相垂直，且∠A等于62°，则∠B的度数为 　28°或152°　．
【分析】分两种情况进行讨论：①∠B为锐角，②∠B为钝角，根据每一种情况，利用平行线的性质和垂直的定义即可求出∠B的度数．
解：根据题意有以下两种情况：
①当∠B为锐角时，

∵AF∥BH，
∴∠1＝∠A＝62°，
∵BG⊥AE，
∴∠B＝90°﹣∠1＝90°﹣62°＝28°，
②当∠B为钝角时，
延长HB交AE于T，

由①可知：∠TBG＝28°，
∴∠HBG＝180°﹣∠TBG＝180°﹣28°＝152°．
综上所述：∠B的度数为28°或152°．
故答案为：28°或152°．
【点评】此题主要考查了平行线的性质，垂直的定义，解答此题的关键是熟练掌握平行线的性质，难点是分类讨论，这也是解答此题的易错点．
16．将一副直角三角板ABC，ADE按如图1所示位置摆放，其中∠ACB＝∠AED＝90°，∠ADE＝∠DAE＝45°，∠BAC＝30°，∠ABC＝60°．若将三角板ADE绕点A按每秒3°的速度顺时针旋转180°，如图2，在此过程中，设旋转时间为t秒，当线段DE与三角板ABC的一条边平行时，t＝　10秒或30秒或40秒　．

【分析】由线段DE与三角板ABC的一条边平行可知有三种情况：（1）当DE∥BC时，点E落在线段AC上，由此可求出旋转角，进而可求出t的值；（2）当DE∥AC时，则∠BAE＝90°，由此可求出旋转角，进而可求出t的值；（3）当DE∥AB，则∠CAE＝90°，由此可求出旋转角，进而可求出t的值．
解：设旋转角为α，则旋转的时间t＝α÷3（秒），
∵在顺时针旋转180°的过程中，线段DE与三角板ABC的一条边平行，
∴有以下三种情况：
（1）当DE∥BC时，
∵∠ACB＝∠AED＝90°
∴点E落在线段AC上时，

∴旋转角α＝∠BAC＝30°，
∴t＝α÷3＝30÷3＝10（秒）；
（2）当DE∥AB时，则∠BAE+∠AED＝180°，

∵∠AED＝90°，
∴∠BAE＝180°﹣∠AED＝90°，
∴旋转角α＝∠BAE＝90°，
∴t＝α÷3＝90÷3＝30（秒）；
（3）当DE∥AC时，则∠CAE+∠AED＝180°，

∵∠AED＝90°，
∴∠CAE＝180°﹣∠AED＝90°
∴旋转角α＝∠BAC+∠CAE＝120°，
∴t＝α÷3＝120÷3＝40（秒）；
综上所述：t＝10秒或30秒或40秒．
故答案为：10秒或30秒或40秒．
【点评】此题主要考查了图形的旋转变换与性质，平行线的判定，解答此题的关键是熟练掌握平行线的判定和性质，难点是利用分类讨论的思想进行分类讨论．
三、解答题（68分）
17．如图，在由边长为1个单位长度的小正方形组成的网格中，给出了格点△ABC（顶点为网格线的交点）．
（1）将△ABC先向左平移5个单位，再向下平移3个单位，得到△A1B1C1，并画出平移后的△A1B1C1；
（2）△ABC的面积为 　　．

【分析】（1）利用平移变换的性质分别作出A，B，C的对应点A1，B1，C1即可；
（2）把三角形的面积看成矩形的面积减去周围的三个三角形面积即可．
解：（1）如图，△A1B1C1即为所求；
（2）△ABC的面积＝2×3﹣×1×3﹣×1×2﹣×1×2＝．
故答案为：．

【点评】本题考查作图﹣平移变换，解题的关键是理解题意，灵活运用所学知识解决问题．
18．（1）+﹣
（2）3﹣||
【分析】（1）原式利用平方根、立方根定义计算即可求出值；
（2）原式利用绝对值的代数意义化简，合并即可得到结果．
解：（1）原式＝﹣3+3+1＝1；
（2）原式＝3﹣+＝4﹣．
【点评】此题考查了实数的运算，熟练掌握运算法则是解本题的关键．
19．解方程：
（1）9（x﹣1）2﹣4＝21；
（2）27（2x﹣1）3＝﹣125．
【分析】（1）将方程变形，再用平方根概念即可解得x的值；
（2）将方程变形，再用立方根概念即可解得x的值．
解：（1）移项合并同类项得：9（x﹣1）2＝25，
两边同除以9得：（x﹣1）2＝，
∴x﹣1＝±，
∴x1＝，x2＝﹣；
（2）∵27（2x﹣1）3＝﹣125，
∴（2x﹣1）3＝﹣，
∴2x﹣1＝﹣，
解得：x＝﹣．
【点评】本题考查利用平方根，立方根概念解方程，解题的关键是掌握平方根，立方根的概念．
20．已知∠1＝∠2，∠3＝∠4，∠5＝∠A，试说明：BE∥CF．
请完善下面解答过程，并填写理由．
解：∵∠3＝∠4（已知），
∴AE∥　BC　（ 　内错角相等，两直线平行　），
∴∠EDC＝　∠5　（两直线平行，内错角相等），
∵∠5＝∠A（已知），
∴∠EDC＝　∠A　（ 　同位角相等，两直线平行　），
∴DC∥AB（同位角相等，两直线平行），
∴∠5+∠ABC＝180°（ 　两直线平行，同旁内角互补　），
即∠5+∠2+∠3＝180°，
∵∠1＝∠2（已知），
∴∠5+∠1+∠3＝180°（等量代换），
即∠BCF+∠3＝180°，
∴BE∥　CF　（ 　同旁内角互补，两直线平行　）．

【分析】按照所给的证明思路，利用平行线的判定与性质定理，完善证明过程即可．
解：∵∠3＝∠4（已知），
∴AE∥BC（内错角相等，两直线平行），
∴∠EDC＝∠5（两直线平行，内错角相等），
∵∠5＝∠A（已知），
∴∠EDC＝∠A（等量代换），
∴DC∥AB（同位角相等，两直线平行），
∴∠5+∠ABC＝180°（两直线平行，同旁内角互补），
即∠5+∠2+∠3＝180°，
∵∠1＝∠2（已知），
∴∠5+∠1+∠3＝180°（等量代换），
即∠BCF+∠3＝180°，
∴BE∥CF（同旁内角互补，两直线平行）．
故答案为：BC；内错角相等，两直线平行；∠5；∠A；同位角相等，两直线平行；两直线平行，同旁内角互补；CF；同旁内角互补，两直线平行．
【点评】此题主要考查了平行线的判定与性质，熟练掌握平行线的判定与性质是解答此题的关键．
21．已知2a+1的算术平方根是5，a+b﹣2的立方根是2，求a+b的平方根．
【分析】直接利用算术平方根以及立方根的定义得出a，b的值，进而利用平方根的定义得出答案．
解：∵2a+1的算术平方根是5，
∴2a+1＝52＝25，
解得：a＝12，
∵a+b﹣2的立方根是2，
∴×12+b﹣2＝23＝8，
解得：b＝4，
∴a+b＝12+4＝16，
故a+b的平方根是±4．
【点评】此题主要考查了立方根以及平方根、算术平方根，正确掌握相关定义是解题关键．
22．如图，直线AB、CD相交于点O，OE⊥OF，∠BOF＝∠BOE+20°，OC平分∠AOE，求∠DOE的度数．

【分析】先根据OE⊥OF，∠BOF＝∠BOE+20°求出∠BOF与∠BOE的度数，从而可以得到∠AOE的度数，再根据角平分线的定义求出∠AOC，然后根据对顶角相等求出∠BOD，与∠BOE相加即可求解．
解：∵OE⊥OF，∠BOF＝∠BOE+20°，
∴∠BOF+∠BOE＝90°，
∴∠BOE＝35°，
∴∠AOE＝180°﹣∠BOE＝145°，
∵OC平分∠AOE，
∴∠AOC＝∠AOE＝×145°＝72.5°，
∴∠BOD＝∠AOC＝72.5°，
∴∠DOE＝∠BOD+∠BOE＝72.5°+35°＝107.5°．
【点评】本题考查了垂线，掌握垂线的性质、对顶角相等的性质，以及角的计算，结合图形先求出∠BOE与∠BOF的度数是解题的关键．
23．如图，已知点E、F在直线AB上，点G在线段CD上，ED与FG交于点H，∠C＝∠EFG，∠CED＝∠GHD．
（1）求证：AB∥CD；
（2）若∠EHF＝75°，∠D＝35°，求∠AEM的度数．

【分析】（1）只要证明∠FGD＝∠EFG即可解决问题．
（2）根据∠AEM＝∠CEF＝∠CED+∠HEF，求出∠CED，∠HEF即可．
【解答】（1）证明：∵∠CED＝∠GHD，
∴CE∥FG，
∴∠C＝∠FGD，
∵∠C＝∠EFG，
∴∠FGD＝∠EFG，
∴AB∥CD．

（2）解：∵CE∥FG，∠EHF＝∠GHD＝75°，
∴∠CED＝∠GHD＝75°，
∵AB∥CD，∠D＝35°，
∴∠HEF＝∠D＝35°，
∴∠AEM＝∠CEF＝∠CED+∠HEF＝75°+35°＝110°．
【点评】本题考查平行线的判定和性质，解题的关键是熟练掌握基本知识，属于中考常考题型．
24．已知：AB∥CD，直线EF交AB于点E，交CD于点F，点G在CD上，点P在直线EF右侧，且在直线AB和CD之间，连接PE、PG．
（1）如图1，连接EG，若EG平分∠PEF，∠BEP+∠PGE＝110°，∠PGD＝∠EFD，∠PGD＝30°，求∠BEP的度数；
（2）如图2，若EF平分∠PEA，∠PGD的平分线GN所在的直线与EF相交于点H，则∠EPG与∠EHG之间的数量关系是什么，并说明理由．

【分析】（1）连接EG，由已知条件可得∠PGE＝110°﹣∠BEP，结合（1）的结论可得∠EPG＝∠BEP+30°，由平行线的性质及角平分线的定义可得∠PEG＝60°﹣∠BEP，再利用三角形的内角和定理可求解∠BEP的度数；
（2）根据EF平分∠PEA，可设∠AEF＝∠PEF＝α，根据四边形内角和可得∠PGD＝180°﹣（360°﹣∠EPG﹣2α）＝∠EPG+2α﹣180°，依据∠EFG是△FGH的外角，可得∠FGH＝∠EFG﹣∠EHG＝α﹣∠EHG，最后依据∠PGD＝2∠FGH，即可得到∠EPG与∠EHG之间的数量关系．
解：（1）如图1，连接EG，

∵∠BEP+∠PGE＝110°，
∴∠PGE＝110°﹣∠BEP，
由（1）知：∠EPG＝∠BEP+∠PGD，
∵∠PGD＝∠EFD，∠PGD＝30°．
∴∠EFD＝60°，∠EPG＝∠BEP+30°，
∵AB∥CD，
∴∠EFD+∠BEF＝180°，
∴∠BEF＝120°，
∵EG平分∠PEF，
∴∠PEG＝∠PEF＝（120°﹣∠BEP）＝60°﹣∠BEP，
∵∠PEG+∠EPG+∠PGE＝180°，
∴60°﹣∠BEP+∠BEP+30°+110°﹣∠BEP＝180°，
解得：∠BEP＝40°；

（2）∵EF平分∠PEA，
∴设∠AEF＝∠PEF＝α，
∵AB∥CD，
∴∠GFE＝∠AEF＝α，
在四边形PGFE中，∠PGF＝360°﹣∠EPG﹣2α，
∴∠PGD＝180°﹣（360°﹣∠EPG﹣2α）＝∠EPG+2α﹣180°，
∵∠EFG是△FGH的外角，
∴∠FGH＝∠EFG﹣∠EHG＝α﹣∠EHG，
又∵GN平分∠PGD，
∴∠PGD＝2NGD＝2∠FGH，
即∠EPG+2α﹣180°＝2（α﹣∠EHG），
整理可得，∠EPG+2∠EHG＝180°．

【点评】本题考查的是平行线的性质，三角形外角性质及角平分线的定义的综合运用，用到的知识点为：两直线平行，同旁内角互补；两直线平行，内错角相等．