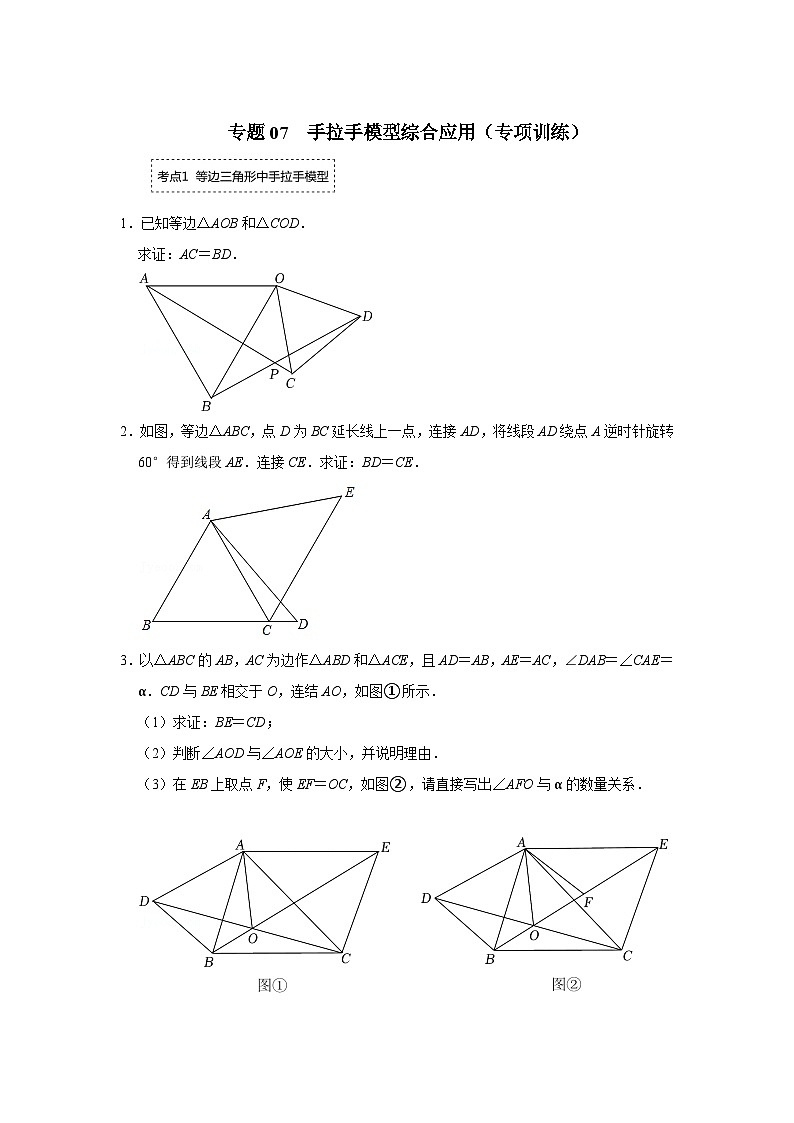
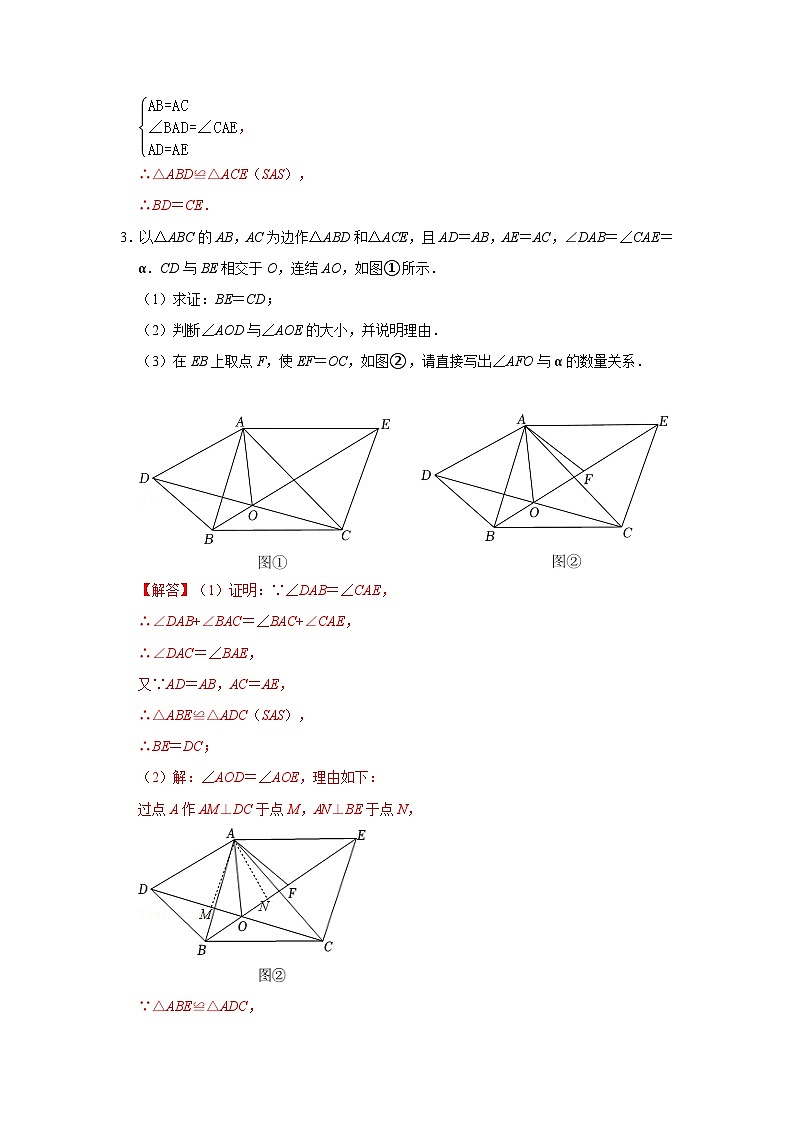
专题07 手拉手模型综合应用（专项训练）-备战中考数学《重难点解读•专项训练》（全国通用）

这是一份专题07 手拉手模型综合应用（专项训练）-备战中考数学《重难点解读•专项训练》（全国通用），文件包含专题07手拉手模型综合应用专项训练解析版docx、专题07手拉手模型综合应用专项训练原卷版docx等2份试卷配套教学资源，其中试卷共22页， 欢迎下载使用。
   专题07  手拉手模型综合应用（专项训练）1．已知等边△AOB和△COD．求证：AC＝BD．【解答】证明：∵△AOB和△COD是等边三角形，∴OA＝OB，OC＝OD，∠AOB＝∠COD＝60°，∴∠AOB+∠BOC＝∠COD+∠BOC，∴∠AOC＝∠BOD，∴△AOC≌△BOD（SAS），∴AC＝BD．2．如图，等边△ABC，点D为BC延长线上一点，连接AD，将线段AD绕点A逆时针旋转60°得到线段AE．连接CE．求证：BD＝CE．【解答】证明：∵△ABC是等边三角形，∴∠BAC＝60°，AB＝AC，由旋转的性质可得：∠DAE＝60°，AD＝AE，∴∠BAC＝∠DAE，∴∠BAD＝∠CAE，在△ABD 和△ACE中，，∴△ABD≌△ACE（SAS），∴BD＝CE．3．以△ABC的AB，AC为边作△ABD和△ACE，且AD＝AB，AE＝AC，∠DAB＝∠CAE＝α．CD与BE相交于O，连结AO，如图①所示．（1）求证：BE＝CD；（2）判断∠AOD与∠AOE的大小，并说明理由．（3）在EB上取点F，使EF＝OC，如图②，请直接写出∠AFO与α的数量关系． 【解答】（1）证明：∵∠DAB＝∠CAE，∴∠DAB+∠BAC＝∠BAC+∠CAE，∴∠DAC＝∠BAE，又∵AD＝AB，AC＝AE，∴△ABE≌△ADC（SAS），∴BE＝DC；（2）解：∠AOD＝∠AOE，理由如下：过点A作AM⊥DC于点M，AN⊥BE于点N，∵△ABE≌△ADC，∴∠ABE＝∠ADC，又∵AD＝AB，∴△ADM≌△ABN（AAS），∴AM＝AN，∵AM⊥OD，AN⊥OE，∴∠AOD＝∠AOE；（3）解：∵△AOD≌△AEB，∴∠AEF＝∠ACO，AE＝AC，又∵EF＝CO，∴△AEF≌△ACO（SAS），∴∠AFE＝∠AOC，AF＝AO，∴∠AFO＝∠AOF＝∠AOD．又∵∠DAB＝∠DOB＝α，∴2∠AFO＝180°﹣α． 4．如图，在△ABC中，∠ACB＝90°，AC＝BC，P是△ABC内一点，且PB＝1，PC＝2，PA＝3，过点C作CD⊥CP，垂足为C，令CD＝CP，连接DP，BD，求∠BPC的度数．【解答】解：∵CD⊥CP，∴∠PCD＝90°，∵PC＝CD＝2，∴△PCD是等腰直角三角形，∴PD＝PC＝2，∠CPD＝∠CDP＝45°，∵∠ACB＝90°，∴∠ACP+∠PCB＝90°，又∵∠PCB+∠BCD＝90°，∴∠ACP＝∠BCD，在△ACP和△BCD中，，∴△ACP≌△BCD（SAS），∴BD＝PA＝3，∵PB＝1，∴PB2+PD2＝12+（2）2＝9，∵PA2＝32＝9，∴PA2＝PB2+PD2，∴∠BPD＝90°，∵∠CPD＝45°，∴∠BPC＝∠BPD+∠CPD＝135°．5．如图，△ABC和△DCE都是等边三角形．（1）如图1，线段BD与AE是否相等？若相等，加以证明；若不相等，请说明理由．（2）如图1，若 B、C、E三点在一条直线上，AE与BD交于点O，求∠BOE的度数．（3）如图2，若 B、C、E三点不在一条直线上，∠ADC＝30°，AD＝4，CD＝3，求BD的长． 【解答】解：（1）BD＝AE，理由如下：∵△ABC和△DCE都是等边三角形．∴BC＝CA，CD＝CE，∠ACB＝∠DCE，∴∠BCD＝∠ACE，∴△BCD≌△ACE（SAS），∴BD＝AE；（2）由△BCD≌△ACE得，∠BDC＝∠AEC，∵∠BOE＝∠ODE+∠DEO＝∠CDE+∠DEC＝60°+60°＝120°，∴∠BOE的度数是120°；（3）∵∠ADC＝30°，∠CDE＝60°，∴∠ADE＝90°，∵CD＝DE＝3，在Rt△ADE中，由勾股定理得，AE＝＝5，由（1）同理得，△BCD≌△ACE，∴BD＝AE＝5．6．如图，△ABC是等边三角形，D为边BC的中点，BE⊥AB交AD的延长线于点E，点F在AE上，且AF＝BE，连接CF、CE．求证：（1）∠CAF＝∠CBE；（2）△CEF是等边三角形．【解答】证明：（1）∵△ABC是等边三角形，∴∠CAB＝∠CBA＝60°，∵D为BC的中点，∴∠CAD＝∠CAB＝30°，又∵BE⊥AB，∴∠ABE＝90°，∴∠CBE＝90°﹣∠CBA＝30°，∴∠CAF＝∠CBE；（2）∵△ABC是等边三角形，∴CA＝CB，在△CAF和△CBE中，，∴△CAF≌△CBE（SAS），∴CE＝CF，∠ACF＝∠BCE，∴∠ECF＝∠BCE+∠BCF＝∠ACF+∠BCF＝∠ACB＝60°，∴△CEF是等边三角形．7．（1）如图1，△ABC和△AMN都是等腰直角三角形，直角顶点为点A，△ABC固定不动，△AMN可以绕着点A旋转．①如图2，将△AMN绕点A旋转，使点M落在BC边上，连接CN．直接写出图中的全等三角形：　    　；直接写出线段CN，CM，CB之间满足的等量关系为：　             　；②如图2，试探索线段MA，MB，MC之间满足的等量关系，并完整地证明你的结论；（2）如图3，P是等腰直角△ABC内一点，∠BAC＝90°，连接PA，PB，PC，将△BAP绕点A顺时针旋转90°后得到△CAQ，连接PQ．已知PA＝2，PB＝3，若∠PQC＝90°，求PC的长． 【解答】解：（1）①∵∠BAM+∠MAC＝90°，∠CAN+∠MAC＝90°，∴∠BAM＝∠CAN，在△BAM和△CAN中：，∴△BAM≌△CAN（SAS），∴BM＝CN，∵BM+CM＝CB，∴CN+CM＝CB，故答案为：△BAM≌△CAN，CN+CM＝CB；②MB2+MC2＝2MA2；证明如下：同理①可证△BAM≌△CAN，∴∠ACN＝∠B＝45°，即∠BCN＝90°，∴CN2+MC2＝MN2，在R△MAN中，MN2＝MA2+AN2＝2MA2，∴MB2+MC2＝2MA2；（2）由旋转知△BAP≌△CAQ，∴PA＝QA＝2，∠PAQ＝∠BAC＝90°，CQ＝BP＝3，∴△PAQ为等腰直角三角形，∴PQ2＝PA2+QA2＝22+22＝8，∵∠PQC＝90°，∴PC2＝PQ2+QC2＝8+32＝17，∴PC＝．8．如图，在平面直角坐标系中，点A的坐标为（1，0），以线段OA为边在第四象限内作等边三角形AOB，点C为x轴正半轴上动点（OC＞1），连接BC，以线段BC为边在第四象限内作等边△CBD，连接DA并延长交y轴于点E．（1）求证：△OBC≌△ABD．（2）在点C的运动过程中，∠CAD的度数是否会变化？如果不变，请求出∠CAD的度数；如果变化，请说明理由．（3）以A，E，C为顶点的三角形是等腰三角形时，直接写出此时点C的坐标和CD的长度．【解答】（1）证明：∵△OAB和△BCD是等边三角形，∴∠OBA＝∠CBD＝60°，OB＝AB，BC＝BD，∴∠OBC＝∠ABD，在△OBC和△ABD中，，∴△OBC≌△ABD（SAS）；（2）解：点C在运动过程中，∠CAD的度数不会变化，理由如下，∵△AOB是等边三角形，∴∠BOA＝∠OAB＝60°，∵△OBC≌△ABD，∴∠BAD＝∠BOA＝60°，∴∠CAD＝180°﹣∠OAB﹣∠BAD＝180°﹣60°﹣60°＝60°，∴点C在运动过程中，∠CAD的度数一直为60°．（3）解：∵∠BOC＝∠BAD＝60°，∠OAB＝60°，∴∠OAE＝180°﹣60°﹣60°＝60°，∴∠EAC＝120°，∠AEO＝30°，∴以A，E，C为顶点的三角形是等腰三角形时，AE和AC为腰，∵OA＝1，∠AEO＝30°，∠AOE＝90°，∴AC＝AE＝2OA＝2，∴OA＝OA+AC＝1+2＝3，∴点C的坐标为（3，0），过点B作BH⊥x轴于点H，则AH＝OA＝AO＝，∠ABH＝30°，∴BH＝＝，CH＝AH+AC＝+2＝，∴BC＝＝，∴CD＝BC＝．9．已知：如图1，△ACB和△DCE均为等边三角形，点A、D、E在同一直线上，连接BE．（1）求证：AD＝BE；（2）求∠AEB的度数；（3）拓展探究：如图2，△ACB和△DCE均为等腰直角三角形，∠ACB＝∠DCE＝90°，点A、D、E在同一直线上，CM为△DCE中DE边上的高，连接BE．①请你直接写出∠AEB的度数为多少度？②探索线段CM、AE、BE之间存在怎样的数量关系，并说明理由．【解答】（1）证明：∵△ACB和△DCE均为等边三角形，∴CA＝CB，CD＝CE，∠ACB＝∠DCE＝60°，∵∠ACB﹣∠DCB＝∠DCE﹣∠DCB，∴∠ACD＝∠BCE．在△ACD和△BCE中，，∴△ACD≌△BCE（SAS），∴AD＝BE；（2）解：∵△ACD≌△BCE，∴∠ADC＝∠BEC，∵△DCE为等边三角形，∴∠CDE＝∠CED＝60°，∵点A、D、E在同一直线上，∴∠ADC＝120°，∴∠BEC＝120°，∴∠AEB＝∠BEC﹣∠CED＝60°；（3）解：①∵△ACB和△DCE均为等腰直角三角形，∴AC＝BC，CD＝CE，∠ACB＝∠DCE＝90°，∠CDE＝∠CED＝45°，∴∠ACB﹣∠DCB＝∠DCE﹣∠DCB，即∠ACD＝∠BCE，在△ACD和△BCE中，，∴△ACD≌△BCE（SAS），∴BE＝AD，∠BEC＝∠ADC，∵点A，D，E在同一直线上，∴∠ADC＝180﹣45＝135°，∴∠BEC＝135°，∴∠AEB＝∠BEC﹣∠CED＝135°﹣45°＝90°；②AE＝BE+2CM．理由：如图2，∵∠DCE＝90°，CD＝CE，CM⊥DE，∴CM＝DM＝EM，∴DE＝DM+EM＝2CM，∵△ACD≌△BCE（已证），∴BE＝AD，∴AE＝AD+DE＝BE+2CM． 10．如图，点G是正方形ABCD对角线CA的延长线上任意一点，以线段AG为边作一个正方形AEFG，线段EB和GD相交于点H．（1）求证：EB＝GD；（2）判断EB与GD的位置关系，并说明理由；（3）若AB＝3，AG＝，求EB的长．【解答】（1）证明：∵四边形EFGA和四边形ABCD是正方形，∴AG＝AE，AB＝AD，∠EAG＝∠DAB＝90°，∵∠GAD＝90°+∠EAD，∠EAB＝90°+∠EAD，∴∠GAD＝∠EAB，在△GAD和△EAB中，，∴△GAD≌△EAB（SAS），∴EB＝GD；（2）解：BE⊥GD，理由如下：如图，设DG与AE的交点为P，∵△GAD≌△EAB，∴∠AEB＝∠AGD，∵∠EPH＝∠APG，∴∠EHG＝∠EAG＝90°，∴EB⊥GD；（2）解：如图2，连接BD，BD与AC交于点O，∵四边形ABCD是正方形，AB＝3，∴DB＝AB＝3，DO＝BO＝，∵AG＝，∴GO＝AO+AG＝，∴DG＝＝＝，∴BE＝DG＝．11.点C为线段AB上一点，分别以AC、BC为边在线段AB的同侧作正方形ACDE和BCFG，连接AF、BD．（1）如图①，AF与BD的数量关系和位置关系分别为 　  　，　    　；（2）将正方形BCFG绕着点C顺时针旋转α角（0°＜α＜360°），①如图②，第（1）问的结论是否仍然成立？请说明理由；②若AC＝4，BC＝，当正方形BCFG绕着点C顺时针旋转到点A、B、F三点共线时，求DB的长度．【解答】解：（1）AF与BD的数量关系和位置关系分别为AF＝BD，AF⊥BD，理由如下：延长AF交BD于H，如图①所示：∵四边形ACDE和四边形BCFG是正方形，∴AC＝CD，CF＝CB，∠ACF＝∠DCB＝90°，∴∠CAF+∠AFC＝90°，在△ACF和△DCB中，，∴△ACF≌△DCB（SAS），∴AF＝BD，∠CAF＝∠CDB，∵∠DFH＝∠AFC，∴∠CDB+∠DFH＝∠CAF+∠AFC＝90°，∴∠DHF＝90°，∴AF⊥BD；故答案为：AF＝BD，AF⊥BD；（2）①第（1）问的结论仍然成立，理由如下：设AF交CD于点M，如图②所示：∵四边形ACDE和四边形BCFG是正方形，∴AC＝CD，CF＝CB，∠ACD＝∠FCB＝90°，∴∠CAF+∠AMC＝90°，∴∠ACD+∠DCF＝∠FCB+∠DCF，即∠ACF＝∠BCD，在△ACF和△DCB中，，∴△ACF≌△DCB（SAS），∴AF＝BD，∠CAF＝∠CDB，∵∠DMH＝∠AMC，∴∠CDB+∠DMH＝∠CAF+∠AMC＝90°，∴∠DHM＝90°，∴AF⊥BD；②分两种情况：a、如图③所示：连接CG交BF于O，∵四边形BCFG是正方形，∴CB＝BG，BF⊥CG，∠BGF＝90°，OB＝OF＝OC＝OG，∴BF＝CG＝BC＝2，OB＝OF＝OC＝BF＝1，∴AO＝＝＝，∴AF＝AO+OF＝+1，由（2）得：AF＝DB，∴DB＝+1；b、如图④所示：连接CG交BF于O，同上得：OB＝OF＝OC＝BF＝1，∴AO＝＝＝，AF＝AO﹣OF＝﹣1，由（2）得：AF＝DB，∴DB＝﹣1；综上所述，当正方形BCFG绕着点C顺时针旋转到点A、B、F三点共线时，DB的长度为+1或﹣1．