专题07 二次函数与直角三角形有关的问题（知识解读）-备战中考数学《重难点解读•专项训练》（全国通用）

专题07 二次函数与直角三角形有关的问题（知识解读）

【专题说明】

二次函数之直角三角形存在性问题，主要指的是在平面直角坐标系下，已知一条边（或两个顶点）的直角三角形存在，求第三个顶点的坐标的题型.主要考察学生对转化思想、方程思想、几何问题代数化的数形结合思想及分类讨论思想的灵活运用。

【解题思路】

直角三角形的存在性问题

1. 找点：在已知两定点，确定第三点构成直角三角形时，要么以两定点为直角顶点，要么以动点为直角顶点.以定点为直角顶点时，构造两条直线与已知直线垂直;以动点为直角顶点时，以已知线段为直径构造圆找点
2. 方法：（1）以两定点为直角顶点时，两直线互相垂直，则k1*k2=-1

     （2） 以已知线段为斜边时，利用K型图，构造双垂直模型，最后利用相似求解，或者三条边分别表示之后，利用勾股定理求解

下面主要介绍2种常用方法：

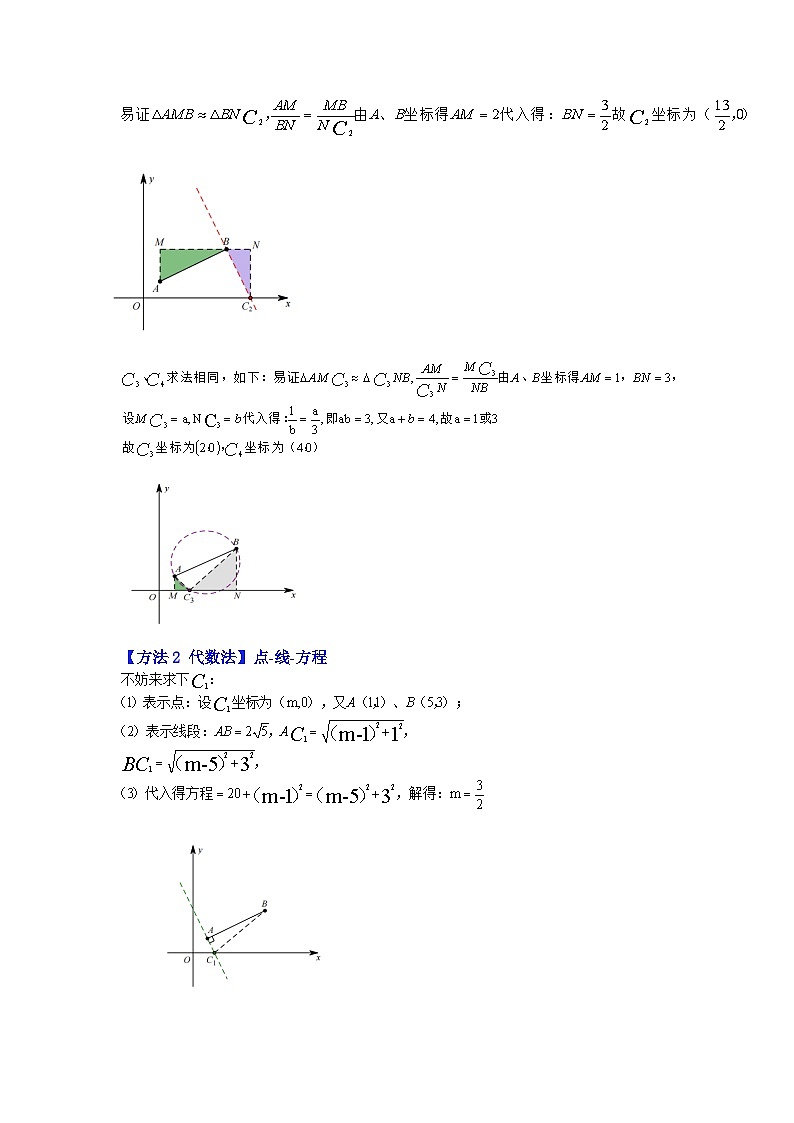
【方法1 几何法】“两线一圆”

（1）若∠A 为直角，过点 A 作 AB 的垂线，与 x 轴的交点即为所求点 C；

（2）若∠B 为直角，过点 B 作 AB 的垂线，与 x 轴的交点即为所求点 C；

（3）若∠C 为直角，以 AB 为直径作圆，与 x 轴的交点即为所求点 C．（直径所对的圆周角为直角）

如何求得点坐标？以为例：构造三垂直．

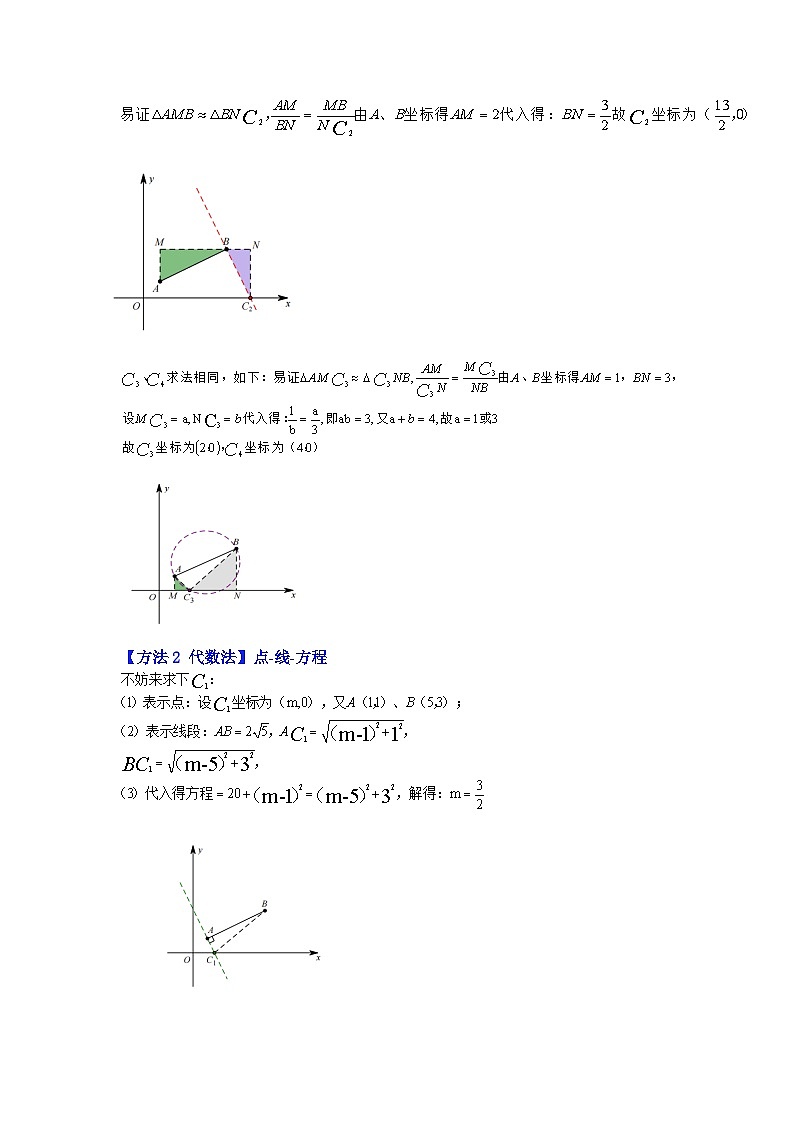
【方法2 代数法】点-线-方程

【典例分析】

【方法1  勾股定理】

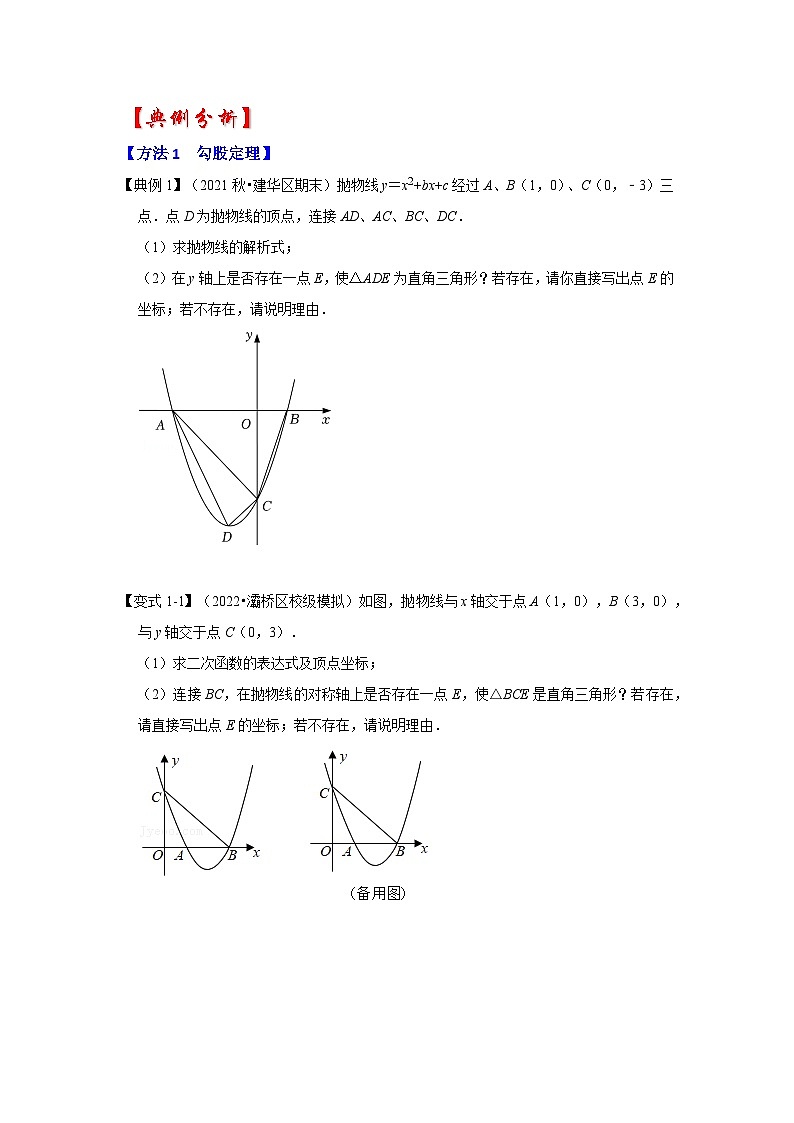
【典例1】（2021秋•建华区期末）抛物线y＝x2+bx+c经过A、B（1，0）、C（0，﹣3）三点．点D为抛物线的顶点，连接AD、AC、BC、DC．

（1）求抛物线的解析式；

（2）在y轴上是否存在一点E，使△ADE为直角三角形？若存在，请你直接写出点E的坐标；若不存在，请说明理由．

【变式1-1】（2022•灞桥区校级模拟）如图，抛物线与x轴交于点A（1，0），B（3，0），与y轴交于点C（0，3）．

（1）求二次函数的表达式及顶点坐标；

（2）连接BC，在抛物线的对称轴上是否存在一点E，使△BCE是直角三角形？若存在，请直接写出点E的坐标；若不存在，请说明理由．

【变式1-2】（2022•广安）如图，在平面直角坐标系中，抛物线y＝ax2+x+m（a≠0）的图象与x轴交于A、C两点，与y轴交于点B，其中点B坐标为（0，﹣4），点C坐标为（2，0）．

（1）求此抛物线的函数解析式．

（2）点P为该抛物线对称轴上的动点，使得△PAB为直角三角形，请求出点P的坐标．

【方法2  构造“K”字型利用相似作答】

【典例2】（2022•碑林区校级四模）如图，在平面直角坐标系中，抛物线C1：y＝ax2+bx+c交x轴于点A（﹣5，0），B（﹣1，0），交y轴于点C（0，5）．

（1）求抛物线C1的表达式和顶点D的坐标．

（2）将抛物线C1关于y轴对称的抛物线记作C2，点E为抛物线C2上一点若△DOE是以DO为直角边的直角三角形，求点E的坐标．

【变式2-1】（2022•济南）抛物线y＝ax2+x﹣6与x轴交于A（t，0），B（8，0）两点，与y轴交于点C，直线y＝kx﹣6经过点B．点P在抛物线上，设点P的横坐标为m．

（1）求抛物线的表达式和t，k的值；

（2）如图1，连接AC，AP，PC，若△APC是以CP为斜边的直角三角形，求点P的坐标；

【变式2-2】（2022•滨州）如图，在平面直角坐标系中，抛物线y＝x2﹣2x﹣3与x轴相交于点A、B（点A在点B的左侧），与y轴相交于点C，连接AC、BC．

（1）求线段AC的长；

（2）若点M为该抛物线上的一个动点，当△BCM为直角三角形时，求点M的坐标．