高中数学人教B版 (2019)选择性必修 第二册3.1.1 基本计数原理第1课时学案

这是一份高中数学人教B版 (2019)选择性必修 第二册3.1.1 基本计数原理第1课时学案，共11页。
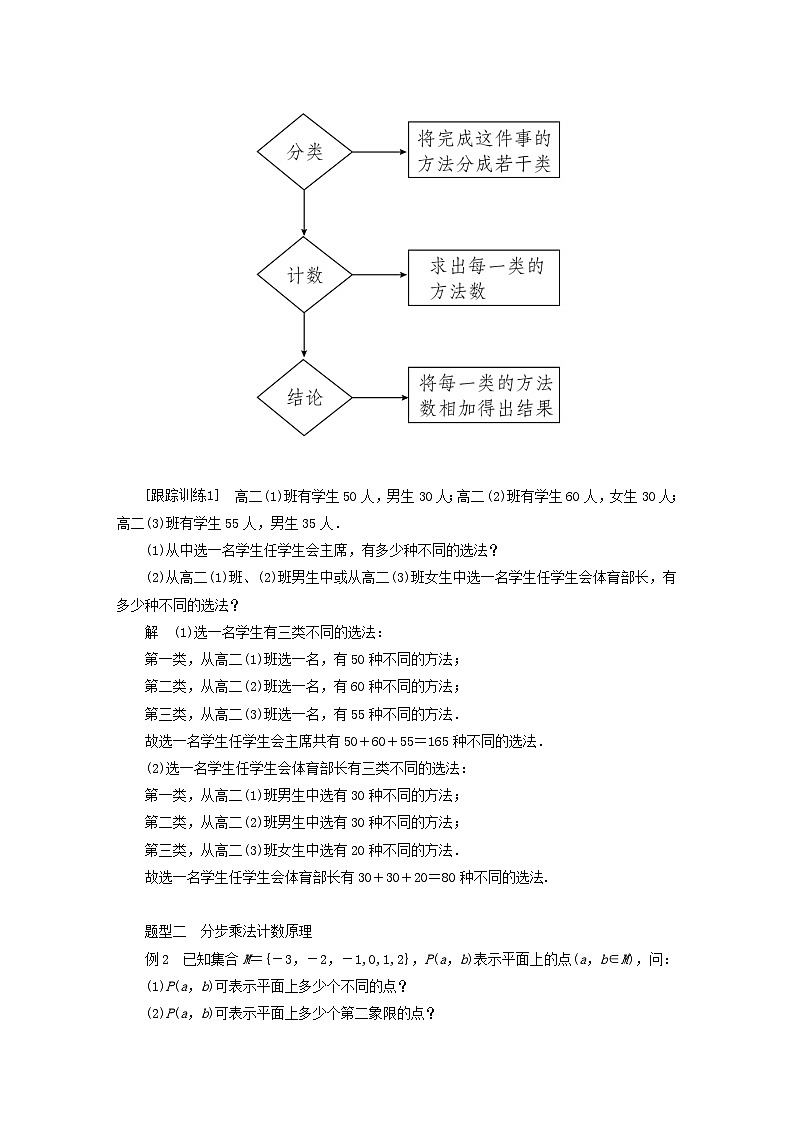
3.1.1　基本计数原理第1课时　分类加法计数原理与分步乘法计数原理及其简单应用(教师独具内容)课程标准：通过实例，了解分类加法计数原理、分步乘法计数原理及其意义．教学重点：理解分类加法计数原理与分步乘法计数原理．教学难点：会利用两个基本原理分析和解决一些简单的实际问题.  知识点一　　　分类加法计数原理完成一件事，如果有n类办法，且：第一类办法中有m1种不同的方法，第二类办法中有m2种不同的方法……第n类办法中有mn种不同的方法，那么完成这件事共有N＝m1＋m2＋…＋mn种不同的方法．知识点二　　　分步乘法计数原理完成一件事，如果需要分成n个步骤，且：做第一步有m1种不同的方法，做第二步有m2种不同的方法……做第n步有mn种不同的方法，那么完成这件事共有N＝m1×m2×…×mn种不同的方法．1．使用分类加法计数原理的条件完成一件事时，若每一类方法中的任一种方法均能将这件事从头到尾完成，则计算完成这件事的方法总数用分类加法计数原理．2．使用分步乘法计数原理的条件完成一件事，若每一步的任一种方法只能完成这件事的一部分，而且必须依次完成所有各步后才能完成这件事，则计算完成这件事的方法总数用分步乘法计数原理．3．使用两个原理解题的本质―→―→―→―→1．判一判(正确的打“√”，错误的打“×”)(1)在分类加法计数原理中，两类不同办法中的方法可以相同．(　　)(2)在分类加法计数原理中，每类办法中的方法都能完成这件事．(　　)(3)在分步乘法计数原理中，任何一个单独的步骤都能完成这件事．(　　)(4)为了给某种新品种选择最佳的生产条件，在分别有4种土质、2种不同的施肥量、3种不同的种植密度、2种不同的播种时间的因素下进行种植试验，则不同的种植方案共有11种．(　　)答案　(1)×　(2)√　(3)×　(4)×2．做一做(请把正确的答案写在横线上)(1)从10名任课教师，54名同学中，选1人参加元旦文艺演出，共有________种不同的选法．(2)一个袋子里放有6个球，另一个袋子里放有8个球，每个球各不相同，从两个袋子里各取一个球，共有________种不同的取法．(3)从3名女同学和2名男同学中选1人主持本班的某次主题班会，则不同的选法有________种．答案　(1)64　(2)48　(3)5 题型一  分类加法计数原理例1　有三个袋子，分别装有不同编号的红色小球6个，白色小球5个，黄色小球4个．若从三个袋子中任取1个小球，有多少种不同的取法？[解]　有三类不同方案：第一类，从第一个袋子中任取1个红色小球，有6种不同的取法；第二类，从第二个袋子中任取1个白色小球，有5种不同的取法；第三类，从第三个袋子中任取1个黄色小球，有4种不同的取法．其中，从这三个袋子的任意一个袋子中取1个小球都能独立地完成“任取1个小球”这件事，根据分类加法计数原理，不同的取法共有6＋5＋4＝15种． 点睛(1)应用分类加法计数原理时，完成这件事的n类方法是相互独立的，无论哪种方案中的哪种方法，都可以独立完成这件事．(2)利用分类加法计数原理解题的一般思路 　高二(1)班有学生50人，男生30人；高二(2)班有学生60人，女生30人；高二(3)班有学生55人，男生35人．(1)从中选一名学生任学生会主席，有多少种不同的选法？(2)从高二(1)班、(2)班男生中或从高二(3)班女生中选一名学生任学生会体育部长，有多少种不同的选法？解　(1)选一名学生有三类不同的选法：第一类，从高二(1)班选一名，有50种不同的方法；第二类，从高二(2)班选一名，有60种不同的方法；第三类，从高二(3)班选一名，有55种不同的方法．故选一名学生任学生会主席共有50＋60＋55＝165种不同的选法．(2)选一名学生任学生会体育部长有三类不同的选法：第一类，从高二(1)班男生中选有30种不同的方法；第二类，从高二(2)班男生中选有30种不同的方法；第三类，从高二(3)班女生中选有20种不同的方法．故选一名学生任学生会体育部长有30＋30＋20＝80种不同的选法.　　题型二  分步乘法计数原理例2　已知集合M＝{－3，－2，－1,0,1,2}，P(a，b)表示平面上的点(a，b∈M)，问：(1)P(a，b)可表示平面上多少个不同的点？(2)P(a，b)可表示平面上多少个第二象限的点？(3)P(a，b)可表示多少个不在直线y＝x上的点？[解]　(1)确定平面上的点P(a，b)可分两步完成：第一步确定a的值，共有6种方法；第二步确定b的值，也有6种方法．根据分步乘法计数原理，得到P(a，b)可表示平面上6×6＝36个不同的点．(2)确定第二象限的点，可分两步完成：第一步确定a，因为a<0，所以有3种方法；第二步确定b，因为b>0，所以有2种方法．由分步乘法计数原              理，得到P(a，b)可表示平面上3×2＝6个第二象限的点．(3)分两步：第一步确定a，有6种方法；第二步确定b，有5种方法．根据分步乘法计数原理，不在直线y＝x上的点共有6×5＝30个． 点睛运用分步乘法计数原理解决问题时的注意点(1)要按事件发生的过程合理分步，即分步是有先后顺序的．(2)各个步骤中的方法互相依存，缺一不可，只有各个步骤都完成了才算完成这件事．   　书架的第一层放有6本不同的数学书，第二层放有6本不同的语文书，第三层放有5本不同的英语书．(1)从这些书中任取一本数学、一本语文和一本英语共三本书的不同取法有多少种？(2)从这些书中任取三本，并且在书架上按次序排好，有多少种不同的排法？解　(1)完成这个工作可分三个步骤：第一步，从第一层中任取一本数学书；第二步，从第二层中任取一本语文书；第三步，从第三层中任取一本英语书．根据分步乘法计数原理，共有6×6×5＝180种不同的取法．(2)本题实际上是从17本书中任取三本放在三个不同位置．完成这个工作分三个步骤：第一步，从17本书中任取一本放在第一个位置上，共有17种不同的方法；第二步，从16本书中任取一本放在第二个位置上，共有16种不同的方法；第三步，从15本书中任取一本放在第三个位置上，共有15种不同的方法．根据分步乘法计数原理，共有17×16×15＝4080种不同的排法.　　题型三  两个基本计数原理的简单应用例3　某校高中三年级一班有优秀团员8人，二班有优秀团员10人，三班有优秀团员6人，学校组织他们去参观某爱国主义教育基地．(1)推选1人为总负责人，有多少种不同的选法？(2)每班选1人为小组长，有多少种不同的选法？(3)从他们中选出2个人管理生活，要求这2个人不同班，有多少种不同的选法？[解]　(1)分三类：第一类是从一班的8名优秀团员中产生，共有8种不同的选法；第二类是从二班的10名优秀团员中产生，共有10种不同的选法；第三类是从三班的6名优秀团员中产生，共有6种不同的选法，由分类加法计数原理可得，共有8＋10＋6＝24种不同的选法．(2)分三步：第一步是从一班的8名优秀团员中选1名组长，共有8种不同的选法；第二步是从二班的10名优秀团员中选1名组长，共有10种不同的选法；第三步是从三班的6名优秀团员中选1名组长，共有6种不同的选法，由分步乘法计数原理可得，共有8×10×6＝480种不同的选法．(3)分三类：每一类又分两步，第一类是从一班、二班的优秀团员中各选1人，有8×10种不同的选法；第二类是从二班、三班的优秀团员中各选1人，有10×6种不同的选法；第三类是从一班、三班的优秀团员中各选1人，有8×6种不同的选法．因此，共有8×10＋10×6＋8×6＝188种不同的选法． 点睛(1)运用两个基本计数原理的关键在于正确区分“分类”与“分步”，分类就是能“一步到位”，即任何一类中任何一种方法，都能完成这件事；而分步只能是“局部到位”，即任何一步中任何一种方法只能完成事件中的某一部分．(2)在既有分类又有分步的题型中，一般先分类，然后在每一类中再分步．   　设有5幅不同的国画，2幅不同的油画，7幅不同的水彩画．(1)从中任选一幅画布置房间，有几种不同的选法？(2)从国画、油画、水彩画中各选一幅布置房间，有几种不同的选法？解　(1)任选一幅画可以分三类：第一类，从国画中选，有5种不同的选法；第二类，从油画中选，有2种不同的选法；第三类，从水彩画中选，有7种不同的选法．根据分类加法计数原理，共有5＋2＋7＝14种不同的选法．(2)从现有的3种画中各选一幅画可以分三步：第一步，从5幅不同的国画中选1幅，有5种不同的选法；第二步，从2幅不同的油画中选1幅，有2种不同的选法；第三步，从7幅不同的水彩画中选1幅，有7种不同的选法．根据分步乘法计数原理，共有5×2×7＝70种不同的选法． 　 　 　 　　　　　 　 　　　　 　 　　1．甲、乙两个班级分别有29名、30名学生，从两个班中选一名学生，则    (　　)A．有29种不同的选法B．有30种不同的选法C．有59种不同的选法D．有29×30种不同的选法答案　C解析　分两类：第一类从甲班选有29种选法，第二类从乙班选有30种选法．由分类加法计数原理得共有29＋30＝59种不同的选法．故选C.2．若5位同学报名参加两个课外活动小组，每位同学限报其中一个小组，则不同的报名方法共有(　　)A．10种  B．20种  C．25种  D．32种答案　D解析　5位同学依次报名，每人均有2种不同的选择，所以共有2×2×2×2×2＝32种不同的报名方法．3．如图，小明从街道的E处出发，先到F处与小红会合，再一起到位于G处的老年公寓参加志愿者活动，则小明到老年公寓可以选择的最短路径条数为(　　)A．24  B．18  C．12  D．9答案　B解析　由题意可知，E→F有6种走法，F→G有3种走法，由分步乘法计数原理知，共有6×3＝18种走法．4．从集合{0,1,2,3,4,5,6}中任取两个互不相等的数a，b组成复数a＋bi，其中虚数有(　　)A．30个  B．42个  C．36个  D．35个答案　C解析　∵a＋bi为虚数，∴b≠0，完成这件事，分两步进行，第一步确定b，有6种不同的方法，第二步确定a，由于a≠b，但a可以为0，故有6种不同的方法，故共有虚数6×6＝36个．5．某公园休息处东面有8个空闲的凳子，西面有6个空闲的凳子，小明与爸爸来这里休息．(1)若小明爸爸任选一个凳子坐下(小明不坐)，有几种坐法？(2)若小明与爸爸分别就坐，有多少种坐法？解　(1)小明爸爸选凳子可以分两类：第一类：选东面的空闲凳子，有8种坐法；第二类：选西面的空闲凳子，有6种坐法．根据分类加法计数原理，小明爸爸共有8＋6＝14种坐法．(2)小明与爸爸分别就坐，可以分两步完成：第一步，小明先就坐，从东西面共8＋6＝14个凳子中选一个坐下，共有14种坐法；(小明坐下后，空闲凳子数变成13)第二步，小明爸爸再就坐，从东西面共13个空闲凳子中选一个坐下，共13种坐法．根据分步乘法计数原理，小明与爸爸分别就坐，共有14×13＝182种坐法． 　 　 　 　　　　　 　 　　　　 　 　　A级：“四基”巩固训练一、选择题1．定义集合A与B的运算A*B如下：A*B＝{(x，y)|x∈A，y∈B}．若A＝{a，b，c}，B＝{a，c，d，e}，则集合A*B中的元素个数为(　　)A．34  B．43  C．12  D．24答案　C解析　由分步乘法计数原理，可知集合A*B中有3×4＝12个元素．故选C.2．某商场共有7个大门，东、南、西侧各2个，北侧1个，1人到该商场购物，则他进出门的走法有(　　)A．8种  B．7种  C．24种  D．49种答案　D解析　完成“进出门”这件事，需分两步，第一步，进商场门，有7种走法；第二步，购物后出门，也有7种走法，根据分步乘法计数原理可得进出门的走法有7×7＝49种．3．某校开设A类选修课4门，B类选修课3门，一名同学从中共选3门．若要求两类课程中各至少选1门，则不同的选法共有(　　)A．30种  B．35种  C．42种  D．48种答案　A解析　设4门A类选修课为A1，A2，A3，A4,3门B类选修课为B1，B2，B3，分两类：第1类，A类1门B类2门，从A类中选1门有4种选法，从B类中选2门有B1B2，B1B3，B2B3,3种选法，所以从A类中选1门B类中选2门有4×3＝12种选法；第2类，A类2门B类1门，从A类中选2门有A1A2，A1A3，A1A4，A2A3，A2A4，A3A4,6种选法，从B类中选1门有3种选法，所以从A类中选2门B类中选1门有6×3＝18种选法．由分类加法计数原理，共有12＋18＝30种选法．4．李芳有4件不同颜色的衬衣、3件不同花样的裙子，另有2套不同样式的连衣裙．“五一”劳动节需选择一套服装参加歌舞演出，则李芳不同的选择穿衣服的方式有(　　)A．24种  B．14种  C．10种  D．9种答案　B解析　不选连衣裙有4×3＝12种方式，选连衣裙有2种方式．共有12＋2＝14种方式．5．(多选)已知集合M＝{1，－2,3}，N＝{－4，5,6，－7}，从两个集合中各取一个元素作为点的坐标，则在平面直角坐标系中，下列说法正确的是(　　)A．第一象限内不同的点有8个B．第二象限内不同的点有7个C．第三象限内不同的点有4个D．第四象限内不同的点有5个答案　AC解析　对于A，此问题可分为两类：①以集合M中的元素作为横坐标，集合N中的元素作为纵坐标，在集合M中只能取1,3两个元素中的一个，方法有2种，在集合N中只能取5,6两个元素中的一个，方法有2种，根据分步乘法计数原理，有2×2＝4个；②以集合N中的元素作为横坐标，集合M中的元素作为纵坐标，在集合N中只能取5,6两个元素中的一个，方法有2种，在集合M中只能取1,3两个元素中的一个，方法有2种，根据分步乘法计数原理，有2×2＝4个．综合①②，利用分类加法计数原理知，共有4＋4＝8个，故A正确；对于B，同理分两类：①以集合M中的元素作为横坐标，集合N中的元素作为纵坐标，有1×2＝2个，②以集合N中的元素作为横坐标，集合M中的元素作为纵坐标，有2×2＝4个，综合①②，共有2＋4＝6个，故B错误；对于C，①以集合M中的元素作为横坐标，集合N中的元素作为纵坐标，有1×2＝2个，②以集合N中的元素作为横坐标，集合M中的元素作为纵坐标，有2×1＝2个，综合①②，共有2＋2＝4个，故C正确；对于D，①以集合M中的元素作为横坐标，集合N中的元素作为纵坐标，有2×2＝4个，②以集合N中的元素作为横坐标，集合M中的元素作为纵坐标，有2×1＝2个，综合①②，共有4＋2＝6个，故D错误．故选AC.二、填空题6．如图，小圆点表示网络的结点，结点之间的连线表示它们由网线相连，连线上标注的数字表示该段网线单位时间内可以通过的最大信息量．现从结点A向结点B传递信息，信息可沿不同的路径同时传递．则单位时间内传递的最大信息量是________．答案　19解析　若以网线为标准，则完成“从结点A向结点B传递信息”这件事也可分为四类，从而分解为若干个简单的问题后再各个击破．分四类：第一类，网线为12→5→3，单位时间内传递的最大信息量是3；第二类，网线为12→6→4，单位时间内传递的最大信息量是4；第三类，网线为12→6→7，单位时间内传递的最大信息量是6；第四类，网线为12→8→6，单位时间内传递的最大信息量是6.根据分类加法计数原理，单位时间内传递的最大信息量是N＝3＋4＋6＋6＝19.7．已知椭圆方程＋＝1，m∈{1,2,3,4,5}，n∈{1,2,3,4,5,6,7}，若椭圆的焦点在x轴上，则椭圆的个数为________；若椭圆的焦点在y轴上，则椭圆的个数为________．答案　10　20解析　若椭圆的焦点在x轴上，则m＞n＞0，考虑m依次取1,2,3,4,5时，符合条件的n值分别有0,1,2,3,4个，由分类加法计数原理知，椭圆的个数为0＋1＋2＋3＋4＝10个．若椭圆的焦点在y轴上，则0<m<n，考虑m依次取1,2,3,4,5时，符合条件的n值分别有6,5,4,3,2个，由分类加法计数原理知，椭圆的个数为6＋5＋4＋3＋2＝20.8.如图，某电子器件是由三个电阻组成的回路，其中有6个焊接点A，B，C，D，E，F，如果某个焊接点脱落，整个电路就会不通．现发现电路不通了，那么焊接点脱落的可能情况共有________种．答案　63解析　电路不通可能是由一个或多个焊接点脱落造成的，问题比较复杂．但电路通的情况只有一种，即各个焊接点均未脱落．因为每个焊接点只有脱落与未脱落两种情况，而只要有一个焊接点脱落，电路就会不通，故焊接点脱落共有26－1＝63种可能情况．三、解答题9．有不同的红球8个，不同的白球7个．(1)从中任意取出一个球，有多少种不同的取法？(2)从中任意取出两个不同颜色的球，有多少种不同的取法？解　(1)由分类加法计数原理，得从中任取一个球共有8＋7＝15种不同的取法．(2)由分步乘法计数原理，得从中任取两个不同颜色的球共有8×7＝56种不同的取法．10．某校高一(4)班有34人，分为四个小组，其中一、二、三、四组分别有7人、8人、9人、10人．(1)若每组选1名组长，有多少种不同的选法？(2)若推选2人发言，这2人需来自不同的组，则有多少种不同的选法？解　(1)分成四步：第一步，一组选1名组长有7种选法；第二步，二组选1名组长有8种选法；第三步，三组选1名组长有9种选法；第四步，四组选1名组长有10种选法．所以每组选1名组长，有7×8×9×10＝5040种不同的选法．(2)分为六类：2人来自一、二组的选法有7×8＝56种；2人来自一、三组的选法有7×9＝63种；2人来自一、四组的选法有7×10＝70种；2人来自二、三组的选法有8×9＝72种；2人来自二、四组的选法有8×10＝80种；2人来自三、四组的选法有9×10＝90种．所以共有56＋63＋70＋72＋80＋90＝431种不同的选法． B级：“四能”提升训练1．标号为A，B，C的三个口袋，A袋中有1个红色小球，B袋中有2个不同的白色小球，C袋中有3个不同的黄色小球，现从中取出2个小球．(1)若取出的两个小球颜色不同，有多少种取法？(2)若取出的两个小球颜色相同，有多少种取法？解　(1)若取出的两个小球颜色不同，则应在A，B袋中各取一个或A，C袋中各取一个或B，C袋中各取一个，故有1×2＋1×3＋2×3＝11种．(2)若取出的两个小球颜色相同，则应在B或C袋中取出两个，故有1＋3＝4种．2．已知集合M＝{－3，－2，－1,0,1,2}，若a，b，c∈M，则：(1)y＝ax2＋bx＋c可以表示多少个不同的二次函数？(2)y＝ax2＋bx＋c可以表示多少个图像开口向上的二次函数？解　(1)y＝ax2＋bx＋c表示二次函数时，a的取值有5种情况，b的取值有6种情况，c的取值有6种情况，因此y＝ax2＋bx＋c可以表示5×6×6＝180个不同的二次函数．(2)当y＝ax2＋bx＋c的图像开口向上时，a的取值有2种情况，b，c的取值均有6种情况，因此y＝ax2＋bx＋c可以表示2×6×6＝72个图像开口向上的二次函数．