数学选择性必修 第一册2.7.2 抛物线的几何性质学案

2.7  抛物线及其方程

2.7.2　抛物线的几何性质

(教师独具内容)

课程标准：1.理解抛物线的几何性质(范围、对称性、顶点、离心率).2.能用抛物线的几何性质分析解决问题．

学法指导：学习本节内容时，首先从实例出发，直观感受抛物线的几何性质，再通过方程精确地、量化地研究抛物线的几何性质．

教学重点：抛物线的几何性质．

教学难点：抛物线的几何性质的应用.

要建造一个圆形花坛水池，池中央有一喷泉，水管高1米，水从喷头P喷出后呈抛物线状，先向上至最高点后落下，最高点距水面2米，水管距抛物线对称轴为1米，问水池直径应如何设计？

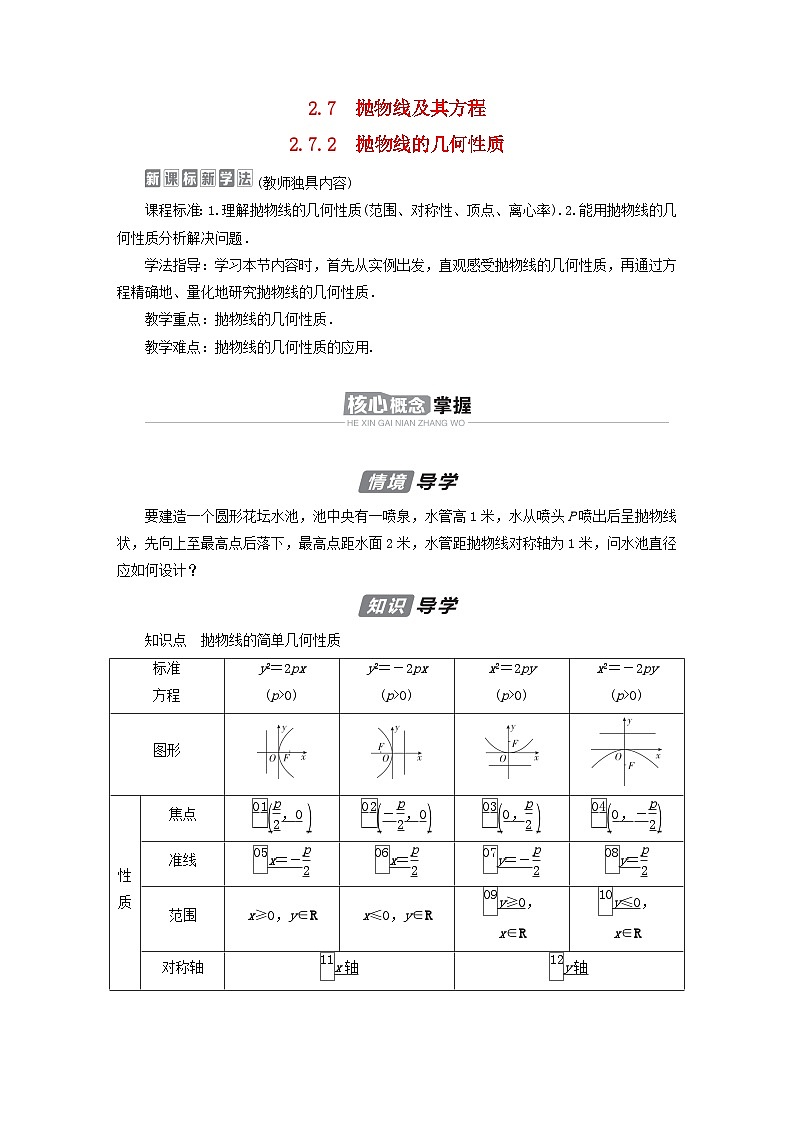
知识点　抛物线的简单几何性质

1．抛物线是圆锥曲线中最为特殊的一种曲线(e＝1)，由于抛物线上任一点到其焦点与到其准线的距离都是相等的，所以应充分利用图形及抛物线的定义进行相互转化，有利于灵活解题．

2．椭圆、双曲线、抛物线在几何性质上的联系与区别

(1)联系：三种曲线都有范围、对称轴、顶点和离心率四个基本的几何性质．

(2)区别：抛物线与椭圆、双曲线相比，主要区别于抛物线的离心率等于1且只有一个焦点、一个顶点、一条对称轴、一条准线，没有中心．就标准方程而言，椭圆、双曲线有两个参数，而抛物线只有一个参数．

另外需注意，抛物线不是双曲线的一支，抛物线无渐近线．

抛物线与双曲线的一支，尽管它们都是不封闭的、有开口的光滑曲线，但是它们的图像性质是完全不同的，事实上，从开口的变化规律来看，双曲线的开口是越来越大，而抛物线的开口越来越趋于扁平．

3．利用抛物线的定义可以得知，抛物线的焦点弦(过焦点的弦)有许多特殊性质：如图，AB是抛物线y2＝2px(p>0)过焦点F的一条弦，设A(x1，y1)，B(x2，y2)，AB的中点M(x0，y0)，直线AB的倾斜角为θ，相应的准线为l，N为准线l与x轴交点．

①A，O，B1三点共线，且B，O，A1三点共线；

②AM1⊥BM1，A1F⊥B1F，M1F⊥AB；

③以AB为直径的圆与准线相切(切点为M1)，以A1B1为直径的圆与AB相切(切点为F)，以AF或BF为直径的圆与y轴相切；

④∠ANF＝∠BNF；

⑤|AF|＝，|BF|＝；

⑥|AB|＝x1＋x2＋p＝2＝；

注意：当θ＝90°时，AB称为抛物线的通径，是焦点弦中最短的．

⑦y1y2＝－p2，x1x2＝，|y1－y2|＝；

⑧kOA·kOB＝－4，O·O＝－p2；

⑨＋＝，＝；

⑩S△AOB＝.

下面证明结论⑤：

由抛物线的定义知，|AF|＝|AA1|，|BF|＝|BB1|.

∵|AA1|＝|NF|＋|AF|cosθ＝p＋|AF|cosθ，

∴|AF|＝p＋|AF|cosθ，∴|AF|＝.

同理|BF|＝.

∴结论⑤成立．

由结论⑤易得结论⑥与⑨.

1．判一判(正确的打“√”，错误的打“×”)

(1)抛物线没有渐近线．(　　)

(2)抛物线有对称轴，无对称中心．(　　)

(3)抛物线的开口大小由抛物线的离心率决定．(　　)

(4)抛物线x2＝y与抛物线y2＝x的离心率相同．(　　)

答案　(1)√　(2)√　(3)×　(4)√

2．做一做(请把正确的答案写在横线上)

(1)抛物线y＝x2的准线方程为________.

(2)顶点在原点，对称轴为x轴，且顶点到焦点的距离为3的抛物线的标准方程为________.

(3)已知点P在抛物线y2＝－5x上，且点A(－3,0)，则|PA|的最小值为________.

答案　(1)y＝－2　(2)y2＝12x或y2＝－12x　(3)

题型一  由抛物线的几何性质求标准方程

例1　抛物线的顶点在原点，对称轴是椭圆＋＝1的短轴所在的直线，抛物线的焦点到抛物线的顶点的距离为4，求抛物线的标准方程及准线方程．

[解]　因为椭圆＋＝1的短轴在x轴上，所以抛物线的对称轴为x轴，设抛物线的标准方程为y2＝2px(p>0)或y2＝－2px(p>0)，

因为抛物线的焦点到抛物线的顶点的距离为4，所以＝4，即p＝8，所以抛物线的标准方程为y2＝16x或y2＝－16x，准线方程分别为x＝－4或x＝4.

求抛物线的标准方程要明确四个步骤

(1)定位置(根据条件确定抛物线的焦点位置及开口方向)；

(2)设方程(根据对称轴和开口方向设出标准方程)；

(3)找关系(根据条件列出关于p的方程)；

(4)得出抛物线的标准方程．

[跟踪训练1]　已知抛物线的顶点在坐标原点，对称轴为x轴，且与圆x2＋y2＝4相交于A，B两点，|AB|＝2，求抛物线的方程．

解　由已知，抛物线的焦点可能在x轴正半轴上，也可能在x轴负半轴上．

故可设抛物线的方程为y2＝ax(a≠0)．

设抛物线与圆x2＋y2＝4的交点为A(x1，y1)，B(x2，y2)．

∵抛物线y2＝ax(a≠0)与圆x2＋y2＝4都关于x轴对称，∴点A与点B关于x轴对称，

∴|y1|＝|y2|且|y1|＋|y2|＝2，

∴|y1|＝|y2|＝，代入圆x2＋y2＝4，得x2＋3＝4，

∴x＝±1，

∴A(±1，)或A(±1，－)，代入抛物线方程，得()2＝±a，∴a＝±3.

∴所求抛物线的方程是y2＝3x或y2＝－3x.

题型二  抛物线的简单几何性质

例2　如图，已知边长为2的等边三角形AOB，O为坐标原点，AB⊥x轴．

(1)求以O为顶点且过点A，B的抛物线方程；

(2)求抛物线的焦点坐标，准线方程及离心率e.

[解]　(1)如图，设AB⊥x轴于E，则由△AOB是等边三角形，且|AB|＝2得E(，0)，∴A(，1)．

设抛物线的方程为y2＝2px(p>0)，

则1＝2·p·，∴2p＝.

∴抛物线的方程为y2＝x.

(2)由(1)知2p＝，∴＝.

∴抛物线的准线方程为x＝－，

焦点坐标为，离心率e＝1.

求抛物线的标准方程及其几何性质的题目，关键是求抛物线的标准方程，若能得出抛物线的标准方程，则其几何性质就会迎刃而解．

[跟踪训练2]　如图所示，抛物线关于x轴对称，它的顶点在坐标原点，点P(1,2)，A(x1，y1)，B(x2，y2)均在抛物线上．

(1)求抛物线的方程及其准线方程；

(2)当PA与PB的斜率存在且倾斜角互补时，证明：直线AB的斜率为定值．

解　(1)由题意可设抛物线的方程为y2＝2px(p>0)，则由点P(1,2)在抛物线上，得22＝2p×1，解得p＝2，

故所求抛物线的方程是y2＝4x，准线方程是x＝－1.

(2)因为PA与PB的斜率存在且倾斜角互补，

所以kPA＝－kPB，即＝－.

又A(x1，y1)，B(x2，y2)均在抛物线上，所以x1＝，x2＝，从而有＝，即＝－，得y1＋y2＝－4，故直线AB的斜率kAB＝＝＝－1.

题型三  抛物线的最值问题

例3　已知抛物线y2＝2x.

(1)设点A的坐标为，求抛物线上距离点A最近的点P的坐标及相应的距离|PA|；

(2)在抛物线上求一点M，使M到直线x－y＋3＝0的距离最短，并求出距离的最小值．

[解]　(1)设抛物线上任一点P的坐标为(x，y)，

则|PA|2＝2＋y2＝2＋.

因为x≥0，故当x＝0时，|PA|min＝，

故距A最近的点的坐标为(0,0)．

(2)设点M(x0，y0)是抛物线y2＝2x上任一点，

则M到直线x－y＋3＝0的距离为

d＝＝＝，

当y0＝1时，dmin＝＝，

所以点M的坐标是.

有关抛物线最值问题的两种解题思路

一是利用抛物线的定义，进行到焦点的距离与到准线的距离的转化，数形结合，用几何意义解决；二是利用抛物线的标准方程，进行消元代换，获得有关距离的含变量的代数关系式，用求目标函数最值的方法解决．

[跟踪训练3]　已知抛物线C的顶点在原点，焦点F在x轴的正半轴上．若抛物线上一动点P到点A与到F距离之和的最小值为4，且点A在抛物线的内部，求抛物线C的标准方程．

解　设抛物线的方程为y2＝2px(p>0)，则其准线为x＝－，过P点作抛物线准线的垂线，垂足为H，由抛物线的定义知，|PH|＝|PF|.当H，P，A三点共线时，|PA|＋|PF|最小．所以|PF|＋|PA|的最小值为＋2＝4，所以p＝4，所以抛物线C的标准方程为y2＝8x.

1．抛物线y＝x2上一点A(x0,2)到其对称轴的距离为(　　)

A．2  B．4

C．6  D．8

答案　B

解析　抛物线的对称轴为y轴，把A(x0,2)代入y＝x2，得x＝16，即|x0|＝4，故点A到y轴的距离为4.

2．若抛物线y2＝x上一点P到准线的距离等于它到顶点的距离，则点P的坐标为(　　)

A．  B．

C．  D．

答案　B

解析　设抛物线的焦点为F，顶点为O，由题意知，点P到焦点F的距离等于它到顶点O的距离，因此点P在线段OF的垂直平分线上，而点F的坐标为，所以点P的横坐标为，代入抛物线的方程得y＝±，故点P的坐标为，故选B.

3．(多选)设抛物线C：y2＝2px(p>0)的焦点为F，准线为l，A为C上一点，以F为圆心，|FA|为半径的圆交l于B，D两点．若∠ABD＝90°，且△ABF的面积为9，则以下结论中正确的是(　　)

A．△ABF是等边三角形

B．|BF|＝3

C．点F到准线的距离为3

D．抛物线C的方程为y2＝6x

答案　ACD

解析　以F为圆心，|FA|为半径的圆交l于B，D两点，∠ABD＝90°，由抛物线的定义可得|AB|＝|AF|＝|BF|，所以△ABF是等边三角形，所以∠FBD＝30°.因为△ABF的面积为|BF|2＝9，所以|BF|＝6.又点F到准线的距离为|BF|sin30°＝3＝p，则该抛物线的方程为y2＝6x.故选ACD.

4．已知A(2,0)，B为抛物线y2＝x上的一点，则|AB|的最小值为________.

答案　

解析　设点B(x，y)，则x＝y2≥0，

所以|AB|＝＝＝＝.所以当x＝时，|AB|取得最小值，且|AB|min＝.

5．设O为坐标原点，F为抛物线y2＝4x的焦点，A为抛物线上一点，若·＝－4，求点A的坐标．

解　由y2＝4x，知F(1,0)．∵点A在y2＝4x上，

∴不妨设A，

则＝，＝.

代入·＝－4，得＋y(－y)＝－4，

化简，得y4＋12y2－64＝0.

∴y2＝4或y2＝－16(舍去)，∴y＝±2.

∴点A的坐标为(1,2)或(1，－2)．

A级：“四基”巩固训练

一、选择题

1．已知点P(6，y)在抛物线y2＝2px(p>0)上，若点P到抛物线焦点F的距离等于8，则焦点F到抛物线准线的距离等于(　　)

A．2  B．1

C．4  D．8

答案　C

解析　因为抛物线y2＝2px(p>0)的准线为x＝－，点P(6，y)为抛物线上的点，所以P到焦点F的距离等于它到准线的距离，所以6＋＝8，所以p＝4，焦点F到抛物线准线的距离等于4.故选C.

2．抛物线y＝－x2上的点到直线4x＋3y－8＝0的距离的最小值是(　　)

A．  B．

C．  D．3

答案　A

解析　设抛物线y＝－x2上一点为(m，－m2)，该点到直线4x＋3y－8＝0的距离为，当m＝时，取得最小值为.故选A.

3．设抛物线的焦点到顶点的距离为3，则抛物线上的点到准线的距离的取值范围是(　　)

A．(6，＋∞)  B．[6，＋∞)

C．(3，＋∞)  D．[3，＋∞)

答案　D

解析　∵抛物线的焦点到顶点的距离为3，∴＝3，即p＝6.又抛物线上的点到准线的距离的最小值为，

∴抛物线上的点到准线的距离的取值范围为[3，＋∞)．

4．设M(x0，y0)为抛物线C：x2＝8y上一点，F为抛物线C的焦点，以F为圆心、|FM|为半径的圆和抛物线C的准线相交，则y0的取值范围是(　　)

A．(0,2)  B．[0,2]

C．(2，＋∞)  D．[2，＋∞)

答案　C

解析　设圆的半径为r，因为F(0,2)是圆心，抛物线C的准线方程为y＝－2，由圆与准线相交知4<r.因为点M(x0，y0)为抛物线C：x2＝8y上一点，所以x＝8y0，又点M(x0，y0)在圆x2＋(y－2)2＝r2上，所以x＋(y0－2)2＝r2>16，所以8y0＋(y0－2)2>16，即有y＋4y0－12>0，解得y0>2或y0<－6，又因为y0≥0，所以y0>2，故选C.

5．(多选)已知抛物线C：y2＝4px(p>0)的焦点为F，过焦点的直线与抛物线分别交于A，B两点，与y轴的正半轴交于点S，与准线l交于点T，且|FA|＝2|AS|，则(　　)

A．|TS|＝2p  B．＝2

C．|BF|＝p  D．|AF|＝p

答案　ABD

解析　过点A作准线l的垂线，垂足为M，AM与y轴交于点N，因为|FA|＝2|AS|，所以＝，所以|AN|＝|OF|＝，所以|AM|＝p，根据抛物线的定义知|AF|＝p，因为|AS|＝|AF|＝p，所以|SF|＝2p，所以|TS|＝2p.根据抛物线的性质：＋＝，所以＋＝，解得|BF|＝4p，所以＝＝2.故选ABD.

二、填空题

6．已知过抛物线y2＝4x的焦点F的直线交抛物线于A，B两点，且|AF|＝2，则|BF|＝________.

答案　2

解析　因为抛物线的方程为y2＝4x，所以p＝2，F(1,0)．又|AF|＝2，所以xA＋＝2，所以xA＋1＝2，所以xA＝1，即AB⊥x轴，F为AB的中点，所以|BF|＝|AF|＝2.

7．对于抛物线y2＝4x上任意一点Q，点P(a,0)都满足|PQ|≥|a|，则a的取值范围是________.

答案　(－∞，2]

解析　设点Q的坐标为.由|PQ|≥|a|，得|PQ|2≥a2，即y＋2≥a2，整理得y(y＋16－8a)≥0.∵y≥0，∴y＋16－8a≥0.即a≤2＋恒成立．而2＋的最小值为2.∴a≤2.

8．以抛物线C的顶点为圆心的圆交C于A，B两点，交C的准线于D，E两点．已知|AB|＝4，|DE|＝2，则C的焦点到准线的距离为________，四边形ABED的面积为________.

答案　4　3＋6

解析　由题意，不妨设抛物线的方程为y2＝2px(p>0)，由|AB|＝4，|DE|＝2，可取A，D，设O为坐标原点，由|OA|＝|OD|，得＋8＝＋5，解得p＝4，故C的焦点到准线的距离为4.易知四边形ABED是梯形，梯形的上底长|DE|＝2，下底长|AB|＝4，高为＋＝3，故四边形ABED的面积为×(2＋4)×3＝3＋6.

三、解答题

9．若抛物线的顶点在原点，开口向上，F为焦点，M为准线与y轴的交点，A为抛物线上一点，且|AM|＝，|AF|＝3，求此抛物线的标准方程．

解　设所求抛物线的标准方程为x2＝2py(p>0)，

设A(x0，y0)，由题意知M.

因为|AF|＝3，所以y0＋＝3，

因为|AM|＝，

所以x＋2＝17，

所以x＝8，代入x＝2py0，得

8＝2p，解得p＝2或p＝4.

所以所求抛物线的标准方程为x2＝4y或x2＝8y.

10．已知抛物线关于x轴对称，它的顶点在坐标原点O，并且经过点M(2，y0)．若点M到该抛物线焦点的距离为3，求抛物线的方程及|OM|的值．

解　设抛物线的方程为y2＝2px(p>0)，

则其焦点坐标为，准线方程为x＝－，

∵M在抛物线上，

∴M到焦点的距离等于其到准线的距离，即

＝＝3.

解得p＝2，y0＝±2，∴抛物线的方程为y2＝4x.

点M(2，±2)，根据两点间距离公式有

|OM|＝ ＝2.

B级：“四能”提升训练

1．已知A，B是抛物线y2＝2px(p>0)上两点，O为坐标原点，若|OA|＝|OB|，且△ABO的垂心恰是此抛物线的焦点F，求直线AB的方程．

解　由已知得抛物线的焦点为F，

∵抛物线关于x轴对称，|OA|＝|OB|，

∴△ABO为等腰三角形．

∴A，B两点关于x轴对称．

设A(x0，y0)，则B(x0，－y0)，

∵△ABO的垂心恰为抛物线的焦点，∴BF⊥OA.

则kBF·kOA＝－1，即·＝－1.

又y＝2px0，∴x0＝p.∴直线AB的方程为x＝.

2．一抛物线拱桥跨度为52 m，水面距拱顶6.5 m，一竹排上载有一宽4 m，高6 m的大木箱，问竹排能否安全通过？

解　如图所示，建立平面直角坐标系，

设抛物线方程为

x2＝－2py(p>0)，

易知A(26，－6.5)，

设B(2，y)，由262＝－2p×(－6.5)得p＝52，

∴抛物线方程为x2＝－104y.

当x＝2时，y＝－，

∵6.5－＝>6，∴竹排能安全通过．