

- 新教材2023年高中数学第1章空间向量与立体几何1.4空间向量的应用1.4.1用空间向量研究直线平面的位置关系第2课时空间中直线平面的垂直素养作业新人教A版选择性必修第一册 试卷 0 次下载
- 新教材2023年高中数学第1章空间向量与立体几何1.4空间向量的应用1.4.2用空间向量研究距离夹角问题第1课时距离问题素养作业新人教A版选择性必修第一册 试卷 0 次下载
- 新教材2023年高中数学第1章空间向量与立体几何综合测试题新人教A版选择性必修第一册 试卷 0 次下载
- 新教材2023年高中数学第2章直线和圆的方程2.1直线的倾斜角与斜率2.1.1倾斜角与斜率素养作业新人教A版选择性必修第一册 试卷 0 次下载
- 新教材2023年高中数学第2章直线和圆的方程2.1直线的倾斜角与斜率2.1.2两条直线平行和垂直的判定素养作业新人教A版选择性必修第一册 试卷 0 次下载
高中数学人教A版 (2019)选择性必修 第一册第一章 空间向量与立体几何1.4 空间向量的应用第2课时测试题
展开第一章 1.4 1.4.2 第2课时
A组·素养自测
一、选择题
1.若平面α的一个法向量为n1=(1,0,1),平面β的一个法向量是n2=(-3,1,3),则平面α与β所成的角等于( D )
A.30° B.45°
C.60° D.90°
[解析] 因为n1·n2=(1,0,1)·(-3,1,3)=0,所以α⊥β,即平面α与β所成的角等于90°.
2.(多选)已知v为直线l的方向向量,n1,n2分别为平面α,β的法向量(α,β不重合),则下列选项中,正确的是( AB )
A.n1∥n2⇔α∥β B.n1⊥n2⇔α⊥β
C.v∥n1⇔l∥α D.v⊥n1⇔l∥α
[解析] 对于A,平面α,β不重合,所以平面α,β的法向量平行等价于平面α,β平行,A正确;对于B,平面α,β不重合,所以平面α,β的法向量垂直等价于平面α,β垂直,B正确;对于C,直线的方向向量平行于平面的法向量等价于直线垂直于平面,C错误;对于D,直线的方向向量垂直于平面的法向量等价于直线平行于平面或直线在平面内,D错误.故选AB.
3.如图所示,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AB=BC=AA1,∠ABC=90°,点E,F分别是棱AB,BB1的中点,则直线EF和BC1的夹角是( C )
A. B.
C. D.
[解析] 如图所示,建立空间直角坐标系Bxyz.
由于AB=BC=AA1,不妨取AB=2,
则B(0,0,0),E(0,1,0),F(0,0,1),C1(2,0,2).
所以=(0,-1,1),=(2,0,2),
所以cos 〈,〉===,
所以异面直线EF和BC1的夹角为.
4.已知正方形ABCD所在平面外一点P,PA⊥平面ABCD,若PA=AB,则平面PAB与平面PCD的夹角为( B )
A.30° B.45°
C.60° D.90°
[解析] 如图所示,建立空间直角坐标系.设PA=AB=1,
则A(0,0,0),D(0,1,0),P(0,0,1),
∴=(0,1,0).
取PD的中点E,
则E,∴=,
易知是平面PAB的一个法向量,是平面PCD的一个法向量,所以cos〈,〉=,故平面PAB与平面PCD的夹角为45°.
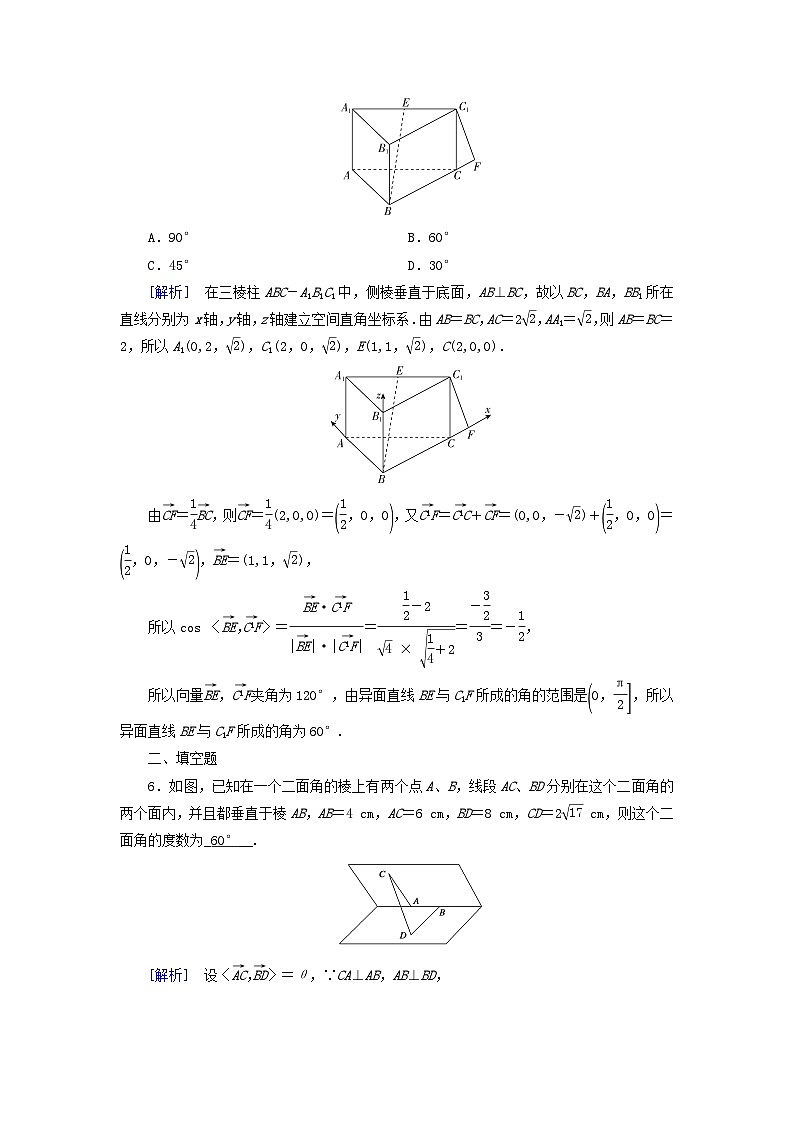
5.(2023·孝感高二检测)在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB⊥BC,AB=BC,AC=2,AA1=,点E为A1C1的中点,点F在BC的延长线上且=,则异面直线BE与C1F所成的角为( B )
A.90° B.60°
C.45° D.30°
[解析] 在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB⊥BC,故以BC,BA,BB1所在直线分别为x轴,y轴,z轴建立空间直角坐标系.由AB=BC,AC=2,AA1=,则AB=BC=2,所以A1(0,2,),C1(2,0,),E(1,1,),C(2,0,0).
由=,则=(2,0,0)=,又=+=(0,0,-)+=,=(1,1,),
所以cos 〈,〉====-,
所以向量,夹角为120°,由异面直线BE与C1F所成的角的范围是,所以异面直线BE与C1F所成的角为60°.
二、填空题
6.如图,已知在一个二面角的棱上有两个点A、B,线段AC、BD分别在这个二面角的两个面内,并且都垂直于棱AB,AB=4 cm,AC=6 cm,BD=8 cm,CD=2 cm,则这个二面角的度数为_60°__.
[解析] 设〈,〉=θ,∵CA⊥AB,AB⊥BD,
∴·=·=0,〈,〉=180°-θ,
∴||2=(++)2
=||2+||2+||2+2||||cos (180°-θ).
∴(2)2=62+42+82+2×6×8×(-cos θ),
∴cos θ=,∴θ=60°.
因此,所求二面角的度数为60°.
7.在空间中,已知平面α过点(3,0,0)和(0,4,0)及z轴上一点(0,0,a)(a>0),如果平面α与平面xOy的夹角为45°,则a= .
[解析] 平面xOy的一个法向量为n=(0,0,1),设平面α的一个法向量为m=(x,y,z),则即3x=4y=az,取z=1,则x=,y=,∴m=.
由题意得|cos〈n,m〉|==.
又因为a>0,所以a=.
8.正方体ABCD-A1B1C1D1中,B1D与BC1夹角的大小是_90°__,若E,F分别为AB,CC1的中点,则异面直线EF与A1C1夹角的大小是_30°__.
[解析] 以点D为坐标原点,建立如图所示的空间直角坐标系,设正方体的棱长为2,则易得D(0,0,0),B(2,2,0),B1(2,2,2),C1(0,2,2),A1(2,0,2),E(2,1,0),F(0,2,1),所以=(-2,0,2),=(-2,-2,-2).因为·=0,所以B1D与BC1夹角的大小是90°.又=(-2,2,0),=(-2,1,1),设异面直线EF与A1C1的夹角为θ,则cos θ==,所以θ=30°.
三、解答题
9.如图,在长方体ABCD-A1B1C1D1中,点E,F分别在棱DD1,BB1上,且2DE=ED1,BF=2FB1.
(1)证明:点C1在平面AEF内;
(2)若AB=2,AD=1,AA1=3,求二面角A-EF-A1的正弦值.
[解析] 设AB=a,AD=b,AA1=c,如图,以C1为坐标原点,的方向为x轴正方向,建立空间直角坐标系C1xyz.
(1)连接C1F,则C1(0,0,0),A(a,b,c),E,F,=,=,得=,
因此EA∥C1F,即A,E,F,C1四点共面,
所以点C1在平面AEF内.
(2)由已知得A(2,1,3),E(2,0,2),F(0,1,1),A1(2,1,0),=(0,-1,-1),=(-2,0,-2),=(0,-1,2),=(-2,0,1).
设n1=(x,y,z)为平面AEF的法向量,则
即
可取n1=(-1,-1,1).
设n2为平面A1EF的法向量,则
同理可取n2=.
因为cos〈n1,n2〉==-,
所以二面角A-EF-A1的正弦值为.
10.(2022·全国乙卷)如图,四面体ABCD中,AD⊥CD,AD=CD,∠ADB=∠BDC,E为AC的中点.
(1)证明:平面BED⊥平面ACD;
(2)设AB=BD=2,∠ACB=60°,点F在BD上,当△AFC的面积最小时,求CF与平面ABD所成的角的正弦值.
[解析] (1)因为AD=CD,∠ADB=∠CDB,DB=DB,所以△ADB≌△CDB,所以AB=BC.
因为E为AC的中点,所以AC⊥BE,AC⊥DE,
又BE∩DE=E,BE,DE⊂平面BED,所以AC⊥平面BED,
又AC⊂平面ACD,所以平面BED⊥平面ACD.
(2)因为AB=BC=2,∠ACB=60°,所以△ABC为正三角形,则AC=2,BE=,AE=1.
因为AD=CD,AD⊥CD,所以△ADC为等腰直角三角形,所以DE=1.
所以DE2+BE2=BD2,则DE⊥BE.
由(1)可知,AC⊥平面BED.连接EF,因为EF⊂平面BED,所以AC⊥EF,当△AFC的面积最小时,点F到直线AC的距离最小,即EF的长度最小.
在Rt△BED中,当EF的长度最小时,EF⊥BD,EF==.
又DE⊥AC,BE⊥AC,所以EA,EB,ED两两垂直,
以E为坐标原点,EA,EB,ED所在的直线分别为x,y,z轴建立如图所示空间直角坐标系E-xyz,则A(1,0,0),B(0,,0),D(0,0,1),C(-1,0,0),=(-1,,0),=(0,,-1).
易得DF=,FB=,所以3=.
设F(0,y,z),则=(0,y,z-1),=(0,-y,-z),
所以3(0,y,z-1)=(0,-y,-z),
得y=,z=,
即F,
所以=.
设平面ABD的法向量为n= (x1,y1,z1),
则,不妨取y1=1,
则x1=,z1=,n=(,1,).
记CF与平面ABD所成的角为α,则sin α=|cos〈,n〉|==.
B组·素养提升
一、选择题
1.正方体ABCD-A1B1C1D1中,动点M在线段A1C上,E,F分别为DD1,AD的中点.若异面直线EF与BM所成的角为θ,则θ的取值范围为( A )
A. B.
C. D.
[解析] 以D点为原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴建立空间直角坐标系.设DA=2,易得=(1,0,-1),设=λ=(2λ,-2λ,2λ)(0≤λ≤1),=(2λ-2,-2λ,2λ),则cos θ=|cos〈,〉|,
即cos θ==
=(0≤λ≤1),
当λ=时,cos θ取到最大值,当λ=1时,cos θ取到最小值,
所以θ的取值范围为,故选A.
2.如图,已知四棱锥P-ABCD的底面ABCD是等腰梯形,AB∥CD,且AC⊥BD,AC与BD交于O,PO⊥底面ABCD,PO=2,AB=2,E,F分别是AB,AP的中点.则平面FOE与平面OEA夹角的余弦值为( B )
A.- B.
C.- D.
[解析] 由题意,以O为坐标原点,OB,OC,OP所在直线分别为x轴,y轴,z轴建立如图所示的空间直角坐标系,由题知,OA=OB=2,
则A(0,-2,0),B(2,0,0),P(0,0,2),∴E(1,-1,0),F(0,-1,1),
∴=(1,-1,0),=(0,-1,1),设平面OEF的法向量为m=(x,y,z),
则即令x=1,可得m=(1,1,1),
易知平面OAE的一个法向量为n=(0,0,1),
则cos〈m,n〉===,设平面FOE与平面OEA夹角为θ,则cos θ=|cos〈m,n〉|=.
3.(多选)如图所示,以等腰直角三角形斜边BC上的高AD为折痕,把△ABD和△ACD折成互相垂直的两个平面后,某学生得出如下四个结论,其中正确的是( BC )
A.AB⊥AC
B.AB⊥DC
C.BD⊥AC
D.平面ADC的法向量和平面ABC的法向量互相垂直
[解析] 以D为坐标原点,DB,DC,DA所在直线分别为x轴,y轴,z轴建立如图所示的空间直角坐标系.
设折叠前的等腰直角三角形ABC的斜边BC=2,则D(0,0,0),B(1,0,0),C(0,1,0),A(0,0,1),则=(1,0,-1),=(0,1,-1),=(0,1,0),=(-1,0,0).从而有·=0+0+1=1,故A错误;·=0,故B正确;·=0,故C正确;易知平面ADC的一个法向量为=(-1,0,0),设平面ABC的法向量为n=(x,y,z),则即令y=1,则x=1,z=1,故n=(1,1,1)为平面ABC的一个法向量,·n=-1,故D错误.故选BC.
4.(多选)(2023·重庆高二检测)在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1=2,E,F分别是BC,A1C1的中点,D在线段B1C1上,则下面说法中正确的有( ACD )
A.EF∥平面AA1B1B
B.若D是B1C1上的中点,则BD⊥EF
C.直线EF与平面ABC所成角的正弦值为
D.直线BD与直线EF所成角最小时,线段BD长为
[解析] 以A为坐标原点,建立空间直角坐标系,如图所示,由题意可得,A(0,0,0),B(2,0,0),C(0,2,0),B1(2,0,2),C1(0,2,2),E(1,1,0),F(0,1,2),
设D(x,2-x,2),故=(-1,0,2),=(x-2,2-x,2),
在直三棱柱ABC-A1B1C1中,∠BAC=90°,
所以为平面AA1B1B的一个法向量,是平面ABC的一个法向量,
对于A,=(0,2,0),所以·=0,即EF⊥AC,又EF⊄平面AA1B1B,所以EF∥平面AA1B1B,故选项A正确;
对于B,若D是B1C1上的中点,则=(-1,1,2),所以·=1+4=5,
所以EF与BD不垂直,故选项B错误;
对于C,因为是平面ABC的一个法向量,=(0,0,2),设直线EF与平面ABC所成的角为α,则sin α=|cos 〈,〉|===,故选项C正确;
对于D,设=λ=(-2λ,2λ,0),(0≤λ≤1),故=+=(-2λ,2λ,2),所以·=2λ+4,
所以|cos 〈,〉|===,
故当=,即λ=时,|cos〈,〉|取得最大值,即直线BD与直线EF所成的角最小,此时=,
所以||=,故选项D正确.
二、填空题
5.已知在长方体ABCD-A1B1C1D1中,AB=1,BC=2,AA1=4,E是侧棱CC1的中点,则直线AE与平面A1ED所成角的正弦值为 .
[解析] 在长方体ABCD-A1B1C1D1中,AB=1,BC=2,AA1=4,E是侧棱CC1的中点,以D为原点,分别以DA,DC,DD1所在直线为x,y,z轴建立空间直角坐标系,A(2,0,0),E(0,1,2),A1(2,0,4),D(0,0,0),=(2,-1,-2),=(2,0,4),=(0,1,2),设平面A1ED的法向量为n=(x,y,z),则n·=2x+4z=0,n·=y+2z=0,取z=1,得n=(-2,-2,1),
设直线AE与平面A1ED所成角为θ,则
sin θ=|cos〈,n〉|===.
∴直线AE与平面A1ED所成角的正弦值为.
6.如图,四面体ABCD中, E,F分别为AB,DC上的点,且AE=BE,CF=2DF,设=a,=b,=c.
(1)以{a,b,c}为基底表示,则= -c+a+b ;
(2)若∠ADB=∠BDC=∠ADC=60°,且||=4,||=3,||=3,则||= .
[解析] (1)如图所示,连接DE.
因为=+,=-=-,=(+),
所以=-c+a+b.
(2)||2=2=a2+b2+c2+a·b-a·c-b·c=×42+×32+×32+×4×3×-×4×3×-×3×3×=.所以||=.
7.如图,在正四棱锥V-ABCD中,二面角V-BC-D为60°,E为BC的中点.已知F为直线VA上一点,且F与A不重合,若异面直线BF与VE所成角为60°,则= 11 .
[解析] O为V的射影,取AB的中点G,以O为坐标原点,分别以OG,OE,OV所在直线为x,y,z轴,建立空间直角坐标系,
设AB=2,则V(0,0,),E(0,1,0),B(1,1,0),A(1,-1,0),
=(1,-1,-),=(1,1,-),=(0,1,-),
设=λ(λ≠1),则=-=(λ-1,-λ-1,-λ+),
由|cos 〈,〉|==,整理得λ2+10λ-11=0,解得λ=-11(λ=1舍),故=11.
三、解答题
8.如图,边长为2的正方形ABCD所在的平面与半圆弧所在平面垂直,M是上异于C,D的点.
(1)证明:平面AMD⊥平面BMC;
(2)当三棱锥M-ABC体积最大时,求平面MAB与平面MCD所成二面角的正弦值.
[解析] (1)由题设知,平面CMD⊥平面ABCD,交线为CD.
因为BC⊥CD,BC⊂平面ABCD,
所以BC⊥平面CMD,故BC⊥DM.
因为M为上异于C,D的点,且DC为直径,所以DM⊥CM.
又BC∩CM=C,所以DM⊥平面BMC.
而DM⊂平面AMD,故平面AMD⊥平面BMC.
(2)以D为坐标原点,的方向为x轴正方向,建立如图所示的空间直角坐标系Dxyz.
当三棱锥M-ABC体积最大时,M为的中点.
由题设得D(0,0,0),A(2,0,0),B(2,2,0),C(0,2,0),M(0,1,1),
=(-2,1,1),=(0,2,0),=(2,0,0).设n=(x,y,z)是平面MAB的一个法向量,则即可取n=(1,0,2).
是平面MCD的一个法向量,
因此cos 〈n,〉==,sin〈n,〉=.
所以平面MAB与平面MCD所成二面角的正弦值是.
9.(2023·福州高二检测)在①PD⊥AB,②∠PCA=∠PCB,③平面PCD⊥平面ABC这三个条件中任选一个,补充在下面问题的横线上,并解答.
问题:已知在三棱锥P-ABC中,D为AB的中点,________,AC=BC=2.
(1)证明:PC⊥AB;
(2)若PC=2,∠PCB=∠ACB=90°,E为线段PB上一点,且EB=3PE,求二面角D-CE-B的余弦值.注:如果选择多个条件分别解答,按第一个解答计分.
[解析] 若选条件①PD⊥AB,
(1)因为AC=BC=2,D为AB的中点;则CD⊥AB;因为PD⊥AB,PD∩CD=D,PD⊂平面PCD,CD⊂平面PCD,
则AB⊥平面PCD;又PC⊂平面PCD,所以PC⊥AB;
(2)因为∠PCB=∠ACB=90°,即PC⊥BC,
又PC⊥AB,AB∩BC=B,AB⊂平面ABC,BC⊂平面ABC,
所以PC⊥平面ABC;因为AC⊂平面ABC,所以PC⊥AC;
则PC,AC,BC两两垂直,以点C为坐标原点,分别以CA,CB,CP所在直线为x轴,y轴,z轴,建立如图所示的空间直角坐标系,
因为PC=2,AC=BC=2,EB=3PE,
则C(0,0,0),A(2,0,0),B(0,2,0),P(0,0,2),所以D(1,1,0),E,
因此=,=(1,1,0),
设平面ECD的一个法向量为m=(x,y,z),
则,所以
不妨令y=-3,则x=3,z=1,即m=(3,-3,1),
又平面BCE显然与x轴垂直,不妨取平面BCE的一个法向量为n=(1,0,0),
则cos〈m,n〉===,
由题意可得,二面角D-CE-B为锐二面角,所以其余弦值为.
若选条件②∠PCA=∠PCB,
(1)由AC=BC=2,∠PCA=∠PCB,PC=PC可得△PCA≌△PCB,则PA=PB,
因为D为AB的中点,所以CD⊥AB,PD⊥AB;
又CD∩PD=D,PD⊂平面PCD,CD⊂平面PCD,所以AB⊥平面PCD;
又PC⊂平面PCD,所以PC⊥AB;
(2)同条件①可得,二面角D-CE-B的余弦值为.
若选条件③平面PCD⊥平面ABC,
(1)因为AC=BC=2,D为AB的中点,则CD⊥AB,
又平面PCD∩平面ABC=CD,所以AB⊥平面PCD;
又PC⊂平面PCD,所以PC⊥AB;
(2)同条件①可得,二面角D-CE-B的余弦值为.
高中数学人教A版 (2019)选择性必修 第一册1.4 空间向量的应用第二课时当堂达标检测题: 这是一份高中数学人教A版 (2019)选择性必修 第一册1.4 空间向量的应用第二课时当堂达标检测题,共9页。
数学选择性必修 第一册第一章 空间向量与立体几何1.4 空间向量的应用第2课时达标测试: 这是一份数学选择性必修 第一册第一章 空间向量与立体几何1.4 空间向量的应用第2课时达标测试,共8页。
人教A版 (2019)选择性必修 第一册1.4 空间向量的应用第1课时同步达标检测题: 这是一份人教A版 (2019)选择性必修 第一册1.4 空间向量的应用第1课时同步达标检测题,共8页。













