2022-2023学年六年级下学期小升初数学期末真题检测卷（北京专用）

这是一份2022-2023学年六年级下学期小升初数学期末真题检测卷（北京专用），共23页。试卷主要包含了表示，个因数，是四棱柱的侧面展开图等内容，欢迎下载使用。
2022-2023学年六年级下学期小升初数学
期末真题检测卷（北京专用）
一．选择题（共15小题）
1．（2022•顺义区）根据下面给出的信息，231可以用（　　）表示。
☆＝1
△＝10
〇＝100
〇△△☆☆☆
表示123
A．〇〇△△△☆ B．〇〇〇☆☆☆△ C．△△〇〇〇☆ D．☆☆〇〇〇△
2．（2022•平谷区）下面用三个7和四个0组成的七位数中，需要读出两个零的是（　　）
A．7007000 B．7070070 C．7700700
3．（2021•丰台区）m和n是不同的质数，m和n的积有（　　）个因数。
A．4 B．3 C．2 D．1
4．（2021•红塔区）赵明在方格纸上画了一个图形，下列描述中正确的是（　　）
①这个图形是一个四边形
②这个图形是一个平行四边形
③这个图形有两条对称轴
④这个图形中有一个直角

A．①④ B．①② C．②③ D．③④
5．（2011•北京）下面图形中（　　）是四棱柱的侧面展开图．
A． B．
C． D．
6．（2022•固始县）下列说法正确的是（　　）
A．一条射线长50米
B．一年中有6个大月，6个小月
C．13：14和4：3能组成比例
7．（2022•顺义区）2021年10月16日零时23分，神舟十三号载人飞船在酒泉卫星发射中心发射升空，零时33分载人飞船与火箭成功分离，进入预定轨道，顺利将3名航天员送入太空，进驻核心舱，进行了为期6个月的驻留，创造了中国航天员连续在轨飞行时长新纪录。为了寻找发射的合适时间，气象学家们查阅和分析了大量的数据，其中最关键的数据是（　　）
A．2021年9月份的天气过程数据
B．2021年1～10月份的天气过程数据
C．2021年10月1日的天气过程数据
D．近5年来10月份的天气过程数据
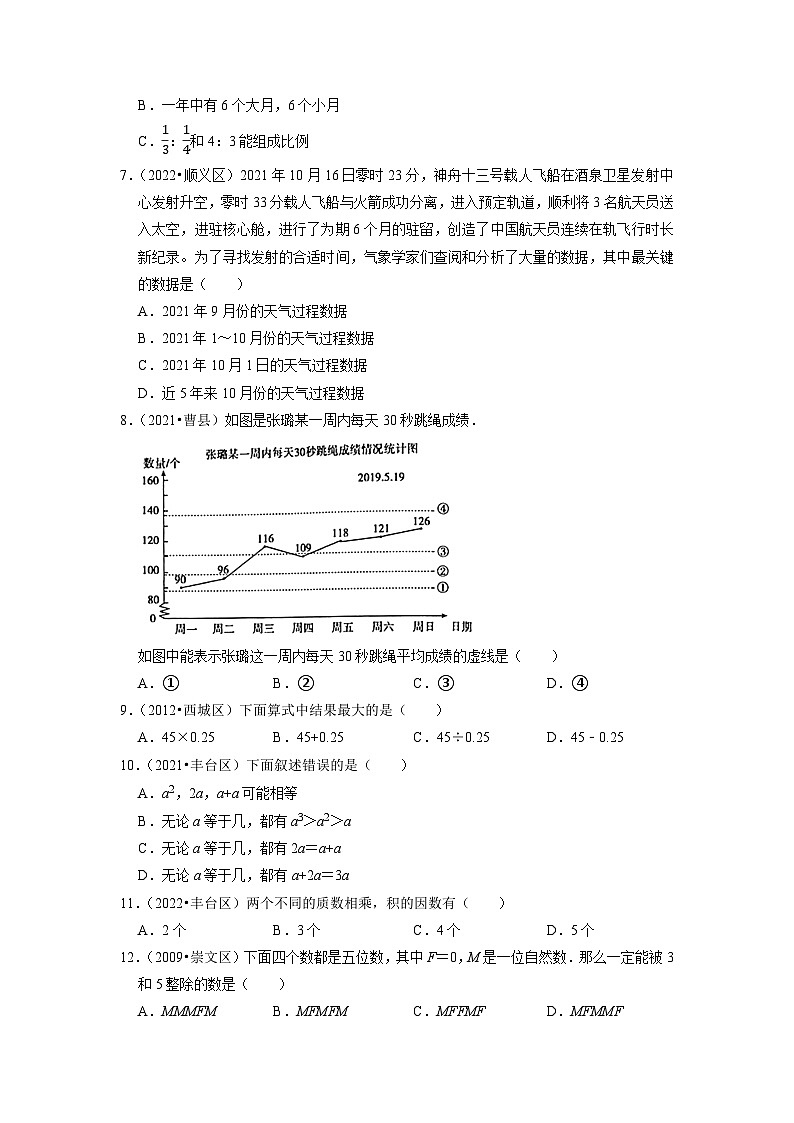
8．（2021•曹县）如图是张璐某一周内每天30秒跳绳成绩．

如图中能表示张璐这一周内每天30秒跳绳平均成绩的虚线是（　　）
A．① B．② C．③ D．④
9．（2012•西城区）下面算式中结果最大的是（　　）
A．45×0.25 B．45+0.25 C．45÷0.25 D．45﹣0.25
10．（2021•丰台区）下面叙述错误的是（　　）
A．a2，2a，a+a可能相等
B．无论a等于几，都有a3＞a2＞a
C．无论a等于几，都有2a＝a+a
D．无论a等于几，都有a+2a＝3a
11．（2022•丰台区）两个不同的质数相乘，积的因数有（　　）
A．2个 B．3个 C．4个 D．5个
12．（2009•崇文区）下面四个数都是五位数，其中F＝0，M是一位自然数．那么一定能被3和5整除的数是（　　）
A．MMMFM B．MFMFM C．MFFMF D．MFMMF
13．（2022•西城区）一个质数和一个合数的最大公因数一定是1。要想说明上面这句话是错误的，可以用下面（　　）作为例子进行反驳。
A．3和4 B．6和8 C．2和10 D．5和7
14．（2011•东城区）非零自然数n与n+1的最小公倍数是（　　）
A．n B．n+1 C．n2+n
15．（2022•顺义区）下面说法表述错误的是（　　）
A．假分数的分数单位都比1大
B．等腰三角形是轴对称图形
C．9既是奇数又是合数
D．水价一定，总价与用水量的关系是正比例关系
二．填空题（共10小题）
16．（2022•昌黎县）在2021年4月24日（第六个“中国航天日”）我国首辆火星车被命名为“祝融号”。在前期的全球征名活动中，共收到有效提名三万九千八百零八个，横线上的数写作 　 　个，省略“万”后面的尾数约是 　 　万个。
17．（2022•东城区）北京市的总面积是一万六千四百一十平方千米，横线上的数写作 　 　平方千米，把它改写成以“万”作单位的数是 　 　万平方千米。
18．（2021•东城区）2022年7月23日，中国首个火星探测器“天问一号”成功发射，2021年2月10日，在经过长达七个月，475000000千米的漫长飞行之后，“天问一号”成功进入火星轨道。将横线上的数改写成以“亿”为单位的数是 　 　亿千米。

19．（2011•延庆县）有一个点，它平移　 　厘米，形成一条40厘米长的线段，这条线段平移　 　厘米，形成一个长40厘米、宽30厘米的长方形．然后沿着它的一条长边旋转一周，形成一个底面直径是　 　厘米，高是　 　厘米的圆柱．
A.30厘米 B.40厘米 C.60厘米 D.80厘米．
20．（2022•朝阳区）用一个放大镜看一个直角，看到的角会　 　．（填“变大”、“不变”或“变小”）
21．（2022•昌平区）观察如图：小蜗牛后面藏的四边形可能是　 　．

22．（2022•长沙县）在一块并排10垄的田地中，选择2垄种植A、B两种作物，每种作物种植一垄．为有利于作物生长，要求A、B两种作物的间隔不小于6垄，则不同的选垄种植方法有　 　种．
23．（2006•延庆县）在一幅条形统计图中，用0.8厘米表示200吨，要表示750吨的数量，直条应当画　 　厘米．
24．（2022•西城区）如果a=20052006，b=20062007，c=20072008，那么a，b，c中最大的是　 　，最小的是　 　．
25．（2014•北京）已知：S=111980+11981+11982+⋯+11991，则S的整数部分是　 　．
三．判断题（共8小题）
26．（2009•崇文区）A、B、C三个自然数，如果A是C的倍数，B也是C的倍数，那么C一定是A和B的最大公约数．　 　．
27．（2021•项城市）一个自然数不是质数就是合数． 　 　（判断对错）．
28．（2022•安阳）0.436扩大10倍与436缩小100倍结果相等．　 　（判断对错）
29．（2011•朝阳区）一条射线长7米．　 　．（判断对错）
30．（2022•广东）一个角的两条边越长，这个角就越大． 　 　（判断对错）
31．（2022•武平县）锐角三角形中，如果一个角是30度，其余两个角可以是55度、95度．　 　．
32．（2011•北京）7400÷80＝740÷8　 　．
33．（2011•朝阳区）一段钢材，锯3段需要12分钟，如果锯成4段需16分钟．　 　（判断对错）
四．计算题（共3小题）
34．（2022•朝阳区）口算.
（1）76+7＝
（2）35﹣8＝
（3）125×4＝
（4）96÷4＝
（5）4.06+4＝
（6）734﹣399＝
（7）700÷5＝
（8）2.8×4×2.5＝
（9）8.67+1.3＝
（10）1﹣0.07＝
（11）6.8+3.2＝
（12）3.2÷0.08＝
（13）0.9+0.1÷0.1＝
（14）25×0.8＝
（15）3.6÷0.4＝
（16）1÷0.125＝
（17）7﹣0.7＝
（18）1.2×0.7＝
（19）17+17=
（20）124+724=
（21）712−512=
（22）911+211=
（23）112+15=
（24）14−15=
（25）1−115=
（26）12÷37=
（27）17×19=
（28）58×35=
（29）17÷37=
（30）59÷35=
35．（2022•郑州）计算
①3.5×[（702﹣270）÷16]
②1+2+3+4+5+…+42+43
③(58−16+34)×24
④0.125×214+214×878+214
36．（2021•北京）计算图中几何体的体积。

五．操作题（共1小题）
37．（2022•鼓楼区）（1）将图形①向上平移4格。
（2）画一条线段将图②分成一个等腰三角形和一个梯形。
（3）画出图②按1：2缩小后的图形。

六．应用题（共10小题）
38．（2022•海淀区）淘气2022年6月1日把1000元存入银行，定期3年，请你根据利率表计算：到期后淘气一共从银行拿回多少钱？
人民币存款利率表
六个月
1.82%
一年
2.1%
三年
3.5%
39．（2022•西城区）育人小学开展“以纸换树，保护环境”的活动，共回收2t废纸。
据统计，每回收5t废纸进行再利用，相当于保护了85棵树。
育人小学回收的废纸进行再利用，相当于保护了多少棵树？
40．（2021•海淀区）淘气今年多少岁？

41．（2022•朝阳区）小军想制作一个三角形框架，他找到了这样的两根木条：

①你认为小军应该锯断哪根木条？写出你的理由．
②小军把这根本条据成长度各是多少的两段（取整厘米数），才能和另外一根木条围成一个三角形呢？
42．（2021•西城区）小明先将两张同样长的长方形卡片分别等分成3份和4份（如图1所示），然后进行了重新拼摆（如图2所示），拼摆后的图形长多少厘米？


43．（2022•东城区）如图所示，依墙而建的“畜禽饲养舍”围成半圆形，其直径为5米。建这个“畜禽饲养舍”需要多长的篱笆？

44．（2022•朝阳区）人工智能（ArtificialIniedligence），英文缩写为AI．它是研究、开发用于模拟、延伸和扩展人的智能的理论、方法、技术及应用系统的一门新的技术科学．如图是2022年我国人工智能企业领域分布情况统计图．

①这三位同学的叙述中，你不认同的是　 　（填写姓名）．
②现在是2022年，你觉得今年我国人工智能企业将在哪个领域的发展最快？请说明你的理由．
45． （2022•海淀区）如图是2010年上海世博会5月1日～7日每天的参观人数统计图．

（1）这7天平均每天的参观人数是多少？
（2）第一天的参观人数比第七天多百分之几？（百分号前保留整数）
46．（2022•东城区）王阿姨把1400mL果汁倒入3个小杯和1个大杯，正好都倒满且无剩余，已知大杯的容积是小杯的2倍，小杯和大杯的容积各是多少毫升？
47．（2022•遂平县）车棚里停放着三轮车和自行车共18辆，它们的轮子数加起来共有42个。三轮车和自行车各有多少辆？


2022-2023学年六年级下学期小升初数学
期末真题检测卷（北京专用）
参考答案与试题解析
一．选择题（共15小题）
1．【答案】A
【分析】根据表格信息，一个〇代表一个百，231里面有2个百，所以应该有2个〇；一个△代表1个十，231十位上是3，表示有三个十，也就是有3个△；231的个位上是1，要有1个☆，据此解答即可。
【解答】解：一个〇代表一个百，231里面有2个百，所以应该有2个〇；一个△代表1个十，231十位上是3，表示有三个十，也就是有3个△；231的个位上是1，要有1个☆，据此可知231应该用〇〇△△△☆表示。
故选：A。
【点评】本题利用图形考查了数的组成，结合题意分析解答即可。
2．【答案】B
【分析】根据整数的读法，从高位到低位，一级一级地读，每一级末尾的0都不读出来，其余数位一个0或连续几个0都只读一个零，即可读出此数；再进行判断，据此解答。
【解答】解：A.7007000读作：七百万七千，一个零也不读；
B.7070070读作：七百零七万零七十，读两个零；
C.7700700读作：七百七十万零七百，读一个零。
所以读出两个零的是7070070。
故选：B。
【点评】本题主要考查整数的读法，要注意0的读法：每一级末尾的0都不读出来，其余数位连续几个0都只读一个零。
3．【答案】A
【分析】根据质数的因数只有1和它本身两个因数，知道m和n只有1和它本身两个因数。再根据找一个数因数的方法，一对一对找出m和n的乘积的因数即可。
【解答】解：m和n为质数，所以m的因数只有1和m，n的因数只有1和n。根据找一个数因数的方法，m和n的乘积的因数有1，m，n和mn，4个因数，所以应选A。
【点评】此题考查了一个质数的因数的特点，和找两个质数乘积的因数的个数的方法。
4．【答案】A
【分析】由图可知，这个图形是一个四边形，但两组对边都不平行，所以不是平行四边形，这个图形有一条对称轴和一个直角，据此解答即可．
【解答】解：这是一个四边形，不是平行四边形，有一条对称轴和一个直角．所以①④正确；
故选：A．
【点评】此题考查了四边形的特征、平行四边形、直角和对称轴条数的辨别方法．
5．【答案】D
【分析】根据：四棱柱的侧面展开图是长方形图；进行解答即可．
【解答】解：由分析知：四棱柱的侧面展开图是长方形图；
故选：D。
【点评】此题应根据四棱柱的侧面展开图，进行分析、解答．
6．【答案】C
【分析】对各题进行依次分析，进而得出答案．
【解答】解：A、因为射线无端点，无限长，所以一条射线长50米，说法错误；
B、一年中有7个大月，大月包括（1.3.5.7.8.10.12）；5个小月，包括2.4.6.9.11；所以一年中有6个大月，6个小月，说法错误；
C、13：14和4：3中，内项之积等于外项之积，所以能组成比例，说法正确；
故选：C．
【点评】解答此题应结合题意，进行认真分析，进而得出结论，用到的知识点：（1）射线的含义及特点；（2）年、月、日及其关系；（3）比例的意义和基本性质．
7．【答案】D
【分析】根据题意，为了寻找发射气象窗口，气象专家们查阅和分析了大量数据，说明这大量的天气信息不是一年或几个月的天气信息，而是长久的天气变化数据，据此解答。
【解答】解：2021年10月16日零时23分，神舟十三号载人飞船在酒泉卫星发射中心发射升空，为了寻找发射气象窗口，气象专家们查阅和分析了大量数据，其中最关键的数据近5年来10月份的天气过程数据。
故选：D。
【点评】本题考查了统计数据在科研方面的应用。
8．【答案】C
【分析】根据平均数的意义可知：一组数的平均数应该比这组数中最大的数小，比最小的数大．所以①和④不对．张璐跳绳的个数大部分在②的上面，所以②的值应该偏低．由此解答即可．
【解答】解：由图可知，④比张璐所跳个数都多，所以不对；
①比张璐所跳个数都少，所以也不对；
张璐所跳个数大部分在②的上方，所以②的值偏小一下，②错．
所以应该选C．
答：图中能表示张璐这一周内每天30秒跳绳平均成绩的虚线是③．
故选：C．
【点评】本题主要考查单式折线统计图的应用，关键运用平均数的意义做题．
9．【答案】C
【分析】计算选项中的各算式的得数，找出结果最大的即可．
【解答】解：45×0.25＝11.25，
45+0.25＝45.25，
45÷0.25＝180，
45﹣0.25＝44.75，
因为11.25＜44.75＜45.25＜180，
所以计算结果最大的是45÷0.25．
故选：C．
【点评】本题根据运算法则求出各个选项的结果，再比较．
10．【答案】B
【分析】根据两个相同的因数相乘，可以写成平方的形式；三个相同的因数相乘，可以写成立方的形式，解答此题即可。
【解答】解：当a＝0时，a2，2a，a+a都相等，题干说法正确；
当a＝0时，a3＝a2＝a，题干说法错误；
无论a等于几，都有2a＝a+a，题干说法正确；
无论a等于几，都有a+2a＝3a，题干说法正确。
故选：B。
【点评】熟练掌握平方和立方的定义，是解答此题的关键。
11．【答案】C
【分析】任意两个不同的质数相乘的积的因数有：这两个质数，1，这两个数的积，可以举例说明。
【解答】解：2和3这两个质数的积是6，6的因数有：1、2、3、6共计4个，
所以任意两个不同的质数相乘的积有：这两个质数，1，这两个数的积共计4个因数。
故选：C。
【点评】本题主要考查两个质数的积的因数的个数，注意两个质数积的因数有4个：这两个质数，1，这两个数的积。
12．【答案】D
【分析】要使这个数一定能被3和5整除，则个位必须为0或5，因M并不一定是5，放在末位并不保险，所以必须个位为F，A、B可排除，同时，要使5位数的5个数字之和被3整除，C＝MFFMF＝M+0+0+M+0＝2M不一定能被3整除，D＝MFMMF＝M+0+M+M+0＝3M可以，因此选D
【解答】解：MFMMF＝M+0+M+M+0＝3M，
故选：D．
【点评】解答此题，要根据能被3和5整除数的特点进行分析，对选项进行排除，然后进行解答．
13．【答案】C
【分析】根据质数与合数的概念，在选项中找出一个质数和一个合数的选项，求出它们的最大公因数即可解答。
【解答】解：一个质数和一个合数的项是C，因为2和10为倍数关系，所以2和10的最大公因数是2，不是1；其它选项不是两个质数就是两个合数。
故选：C。
【点评】熟练掌握合数与质数的意义以及为倍数关系的两个数的最大公因数的求法是解题的关键。
14．【答案】C
【分析】由n与n+1是相邻的两个非零自然数，可知n和n+1是互质数，根据互质数的最小公倍数是它们的乘积，据此解答．
【解答】解：n与n+1是相邻的两个非零自然数，
它们的最小公倍数是：n（n+1）＝n2+n；
故选：C．
【点评】解答本题关键是理解：相邻的两个非零自然数是互质数，它们的最小公倍数是它们的乘积．
15．【答案】A
【分析】根据奇数与偶数、质数与合数的意义，在自然数中，是2的倍数的数叫做偶数，不是2的倍数的数叫做奇数；一个自然数，如果只有1和它本身两个因数，这样的数叫做质数，一个自然数，如果除了1和它本身还有别的因数，这样的数叫做合数。分子大于或者等于分母的分数叫假分数。把单位“1”平均分成若干份取其中的一份的数，叫做分数单位。
【解答】解：分数单位都比1小，所以假分数的分数单位都比1大表述错误；
等腰三角形的两条边相等，两个底角相等，是轴对称图形，所以等腰三角形是轴对称图形表述正确；
9既是奇数又是合数表述正确；
水价一定，总价与用水量的关系是正比例关系表述正确。
故选：A。
【点评】此题主要考查了奇数、偶数，以及质数、合数的认识，轴对称图形和正比例关系，要熟练掌握它们的特征。
二．填空题（共10小题）
16．【答案】39808；4。
【分析】根据整数的写法，从高位到低位，一级一级地写，哪一个数位上一个单位也没有，就在那个数位上写0，即可写出此数；
省略“万”后面的尾数，就是四舍五入到万位，就是把万位后的千位上的数进行四舍五入，再在数的后面写上“万”字，据此解答。
【解答】解：三万九千八百零八写作：39808；
39808≈4万。
答：横线上的数写作：39808个，省略“万”后面的尾数约是4万个。
故答案为：39808；4。
【点评】本题主要考查整数的写法和求近似数，写数时要注意零的写法，求近似数时要注意带计数单位。
17．【答案】16410，2。
【分析】根据整数的写法，从高位到低位，一级一级地写，哪一个数位上一个单位也没有，就在那个数位上写0，即可写出此数；改写成用“万”作单位的数，就是在万位数的右下角点上小数点，然后把小数末尾的0去掉，再在数的后面写上“万”字。
【解答】解：一万六千四百一十写作：16410
16410≈2万
故答案为：16410，2。
【点评】本题考查了整数的写法和数的改写，数的改写时要注意带计数单位。
18．【答案】4.75。
【分析】改写成以“亿”为单位的数，就是在亿位数的右下角点上小数点，然后把小数末尾的0去掉，在数的后面带上“亿”字，据此解答。
【解答】解：475000000千米＝4.75亿千米
答：将横线上的数改写成以“亿”为单位的数是4.75亿千米。
故答案为：4.75。
【点评】本题主要考查整数的改写，注意改写时要带计数单位。
19．【答案】见试题解答内容
【分析】根据平移的知识可知：有一个点，它平移40厘米，形成一条40厘米长的线段，这条线段平移30厘米，形成一个长40厘米、宽30厘米的长方形；
沿着它的一条长边（40厘米）旋转一周，形成一个底面半径是30厘米（底面直径是60厘米），高是40厘米的圆柱；据此解答即可．
【解答】解：有一个点，它平移40厘米，形成一条40厘米长的线段，这条线段平移30厘米，形成一个长40厘米、宽30厘米的长方形．然后沿着它的一条长边旋转一周，形成一个底面直径是60厘米（底面半径30厘米），高是40厘米的圆柱；
故选：B，A，C，B．
【点评】此题考查了平移的知识及平面图形旋转可以得到立体图形，体现了面动成体的运动观点．
20．【答案】不变。
【分析】用一个放大镜看一个直角，只是把角的两条边的长度放大了，度数不变（整体形状不变）；据此解答即可。
【解答】解：用一个放大镜看一个直角，看到的角会不变。
故答案为：不变。
【点评】解答此题应根据角的意义和特征进行解答。
21．【答案】见试题解答内容
【分析】根据图示，小蜗牛后面藏的四边形的露出的两个角都是直角，另两个角可能都是直角，也可能都不是直角，所以小蜗牛后面藏的四边形可能是长方形或梯形．
【解答】解：小蜗牛后面藏的四边形可能是长方形或梯形．
故答案为：长方形或梯形．
【点评】此题主要考查了四边形的特点、分类和识别，要熟练掌握，解答此题的关键是要明确：长方形的每个角都是直角，梯形只有一组平行的边．
22．【答案】见试题解答内容
【分析】如图所示，满足条件的情况有6种可能，当A或B种在第一垄，要求A、B两种作物的间隔不小于6垄，则B或A有3种可能，即种在第八或第九或第十垄；
当A或B种在第二垄，要求A、B两种作物的间隔不小于6垄，则B或A有2种可能，即种在第九或第十垄；
当A或B种在第三垄，要求A、B两种作物的间隔不小于6垄，则B或A有1种可能，即种在第十垄；因此得解．
【解答】解：（3+2+1）×2＝6×2＝12（种）；
答：则不同的选垄种植方法有 12种．
故答案为：12．
【点评】此题考查了简单的排列、组合．分类完成工作，每一类中的方法可以独立完成工作，用加法．
23．【答案】见试题解答内容
【分析】根据题意，可用750吨除以200吨计算出750里面有几个200，然后再乘0.8即可得到答案．
【解答】解：750÷200×0.8
＝3.75×0.8，
＝3（厘米），
答：直条应当画3厘米．
故答案为：3．
【点评】解答此题的关键是确定750吨里面有几个200吨，有几个200吨就有几个0.8厘米．
24．【答案】见试题解答内容
【分析】根据题意，a=20052006=1−12006，b=20062007=1−12007，c=20072008=1−12008，再根据分数大小的比较方法进行解答即可．
【解答】解：a=20052006=1−12006，b=20062007=1−12007，c=20072008=1−12008
12006＞12007＞12008
所以20052006＜20062007＜20072008
答：么a，b，c中最大的是 20072008，最小的是 20052006．
故答案为：20072008，20052006．
【点评】本题考查了对有理数的大小比较法则的应用，能选择适当的方法比较两个数的大小是解答此题的关键．
25．【答案】见试题解答内容
【分析】此题分母有12个加数，这12个分数的和一定小于12个11980，大于12个11991，S的值一定大于12个11980的和的倒数，小于12个11991的和的倒数，据此确定出取值范围即可解答．
【解答】解：分母的加数如果全是11980，那么S=1121980=165，
如果全是111991，那么结果是S=1121991=1651112，
所以165＜S＜1651112，
于是S的整数部分是165．
故答案为：165．
【点评】此题较难，应对分母进行分析，进而确定分母的取值范围，继而得出答案．
三．判断题（共8小题）
26．【答案】×
【分析】根据题意“A是C的倍数，B是C的倍数”可知：C是A的约数，C也是B的约数，那么C一定是A和B的公约数，但不一定是A和B的最大公约数，例如：4是2的倍数，8也是2的倍数，但2不是4和8的最大公约数；进而得出结论．
【解答】解：由分析知：C是A的约数，C也是B的约数，那么C一定是A和B的公约数，但不一定是A和B的最大公约数，
例如：4是2的倍数，8也是2的倍数，但2不是4和8的最大公约数；
故答案为：×．
【点评】解答此题的关键：认真审题，结合题意，并根据因数和倍数的意义，进行解答即可．
27．【答案】×
【分析】根据质数与合数的意义：一个自然数，如果只有1和它本身两个因数，这样的数叫做质数；一个自然数，如果除了1和它本身还有别的因数，这样的数叫做合数．1既不是质数也不是合数．
【解答】解：根据分析：质数与合数是按照一个自然数的因数的个数的多少进行分类，因为1只有一个因数是它本身，所以1既不是质数也不是合数．
因此所有的自然数不是质数就是合数．这种说法是错误的．
故答案为：×．
【点评】此题考查的目的是理解质数与合数的意义，明确：质数与合数是按照一个自然数的因数的个数的多少进行分类．
28．【答案】见试题解答内容
【分析】先算出0.436扩大10倍是多少，就是把0.436的小数点向右移动一位；再算出436缩小100倍是多少，就是把436的小数点向左移动两位；分别算出结果后再进行比较．
【解答】解：0.436×10＝4.36，
436÷100＝4.36，
因为4.36＝4.36，
所以0.436扩大10倍与436缩小100倍结果相等．
故判断为：正确．
【点评】此题主要考查小数点位置移动引起数的大小变化规律：把一个数扩大（或缩小）10倍、100倍、1000倍…，只要把这个数的小数点向右（或向左）移动一位、两位、三位…，反之也成立．
29．【答案】见试题解答内容
【分析】射线只有一个端点，向一方无限延长，所以不能度量长度；据此判断．
【解答】解：因为射线只有一个端点，向一方无限延长，所以不能度量长度，
所以说一条射线长7米是错误的．
故答案为：×．
【点评】此题主要考查对射线的认识，应注意基础知识的积累．
30．【答案】×
【分析】依据角的定义就可填出正确答案．
【解答】解：角的大小和边长无关．
故答案为：×．
【点评】此题主要考查角的定义．
31．【答案】见试题解答内容
【分析】依据三角形的内角和是180度，将三个角的度数相加，若等于180度，则正确，否则，不正确．但是，还应满足每个角都是锐角．
【解答】解：因为30°+55°+95°，
＝85°+95°，
＝180°；
但是95°的角不是锐角，
所以这种说法是错误的．
故答案为：×．
【点评】此题主要考查三角形的内角和定理以及锐角三角形的定义．
32．【答案】见试题解答内容
【分析】根据商不变的性质，在除法算式中，被除数和除数同时扩大或缩小相同的倍数（0除外），商不变，算式中的被除数7400与除数80同时缩小10倍所以商不变．
【解答】解：7400÷80＝740÷8中的被除数7400与除数80同时缩小10倍所以商不变；
故答案为：√．
【点评】此题主要考查的是商不变的性质．
33．【答案】见试题解答内容
【分析】锯3段，需要锯3﹣1＝2次，由此求出锯1次需要的时间是：12÷2＝6（分钟），锯4段需要锯4﹣1＝3次，由此利用乘法的意义即可解答．
【解答】解：12÷（3﹣1）×（4﹣1）
＝12÷2×3
＝18（分钟）
答：需要18分钟．
故答案为：×．
【点评】解答此题的关键是：抓住锯的次数＝锯出的段数﹣1．
四．计算题（共3小题）
34．【答案】83，27，500，24，8.06，335，140，28，9，97，0，93，10，40，1.9，20，9，8，6.3，0.84，27，13，16，1，1760，120，1415，28，163，38，13，2527。
【分析】根据整数、小数以及分数加减乘除法的计算方法直接进行口算即可。
【解答】解：
（1）76+7＝83
（2）35﹣8＝27
（3）125×4＝500
（4）96÷4＝24
（5）4.06+4＝8.06
（6）734﹣399＝335
（7）700÷5＝140
（8）2.8×4×2.5＝28
（9）8.67+1.3＝9.97
（10）1﹣0.07＝0.93
（11）6.8+3.2＝10
（12）3.2÷0.08＝40
（13）0.9+0.1÷0.1＝1.9
（14）25×0.8＝20
（15）3.6÷0.4＝9
（16）1÷0.125＝8
（17）7﹣0.7＝6.3
（18）1.2×0.7＝0.84
（19）17+17=27
（20）124+724=13
（21）712−512=16
（22）911+211=1
（23）112+15=1760
（24）14−15=120
（25）1−115=1415
（26）12÷37=28
（27）17×19=163
（28）58×35=38
（29）17÷37=13
（30）59÷35=2527
【点评】本题属于基本的计算，在平时注意积累经验，逐步提高运算的速度和准确性。
35．【答案】见试题解答内容
【分析】①先算小括号里面的减法，再算中括号里面的除法，最后计算括号外面的乘法；
②这是一个等差数列，数列的首项是1，末项是43，公差是1，根据高斯求和公式就可以直接求出等差数列的和；
③运用乘法的分配律进行简算；
④运用乘法的分配律进行简算．
【解答】解：①3.5×[（702﹣270）÷16]
＝3.5×[432÷16]
＝3.5×27
＝94.5

②1+2+3+4+5+…+42+43
＝（1+43）×43÷2
＝44×43÷2
＝946

③(58−16+34)×24
=58×24−16×24+34×24
＝15﹣4+18
＝29

④0.125×214+214×878+214
＝（18+878+1）×214
＝10×214
＝22.5
【点评】完成本题要注意分析式中数据，运用合适的简便方法计算．
36．【答案】301.44cm3。
【分析】根据图示，该几何体是由一个圆锥和一个圆柱组合而成的，所以该几何体的体积＝圆锥体积+圆柱体积，根据圆锥的体积公式：V=13πr2h，圆柱的体积公式：V＝πr2h，把数据代入公式解答。
【解答】解：8÷2＝4（cm）
3.14×4²×4+13×3.14×4²×6
＝3.14×64+3.14×32
＝3.14×96
＝301.44（cm3）
答：图中几何体的体积是301.44cm3。
【点评】此题主要考查圆锥、圆柱体积公式的灵活运用，关键是熟记公式。
五．操作题（共1小题）
37．【答案】见试题解答内容
【分析】（1）根据图形平移的性质，图形平移后，图形的形状和大小不变，只是图形的位置发生了变化。据此画出平移后的图形。
（2）根据等腰三角形和梯形的特征，画一条线段将图②分成一个等腰三角形和一个梯形即可。
（3）根据图形缩小的方法，先分别求出缩小到原来的12后，长方形的长和宽各是多少，据此画出缩小后的图形。据此解答。
【解答】解：根据要求，作图如下：

【点评】此题考查的目的是理解掌握图形平移的性质及应用，图形放大的方法及应用，结合题意分析解答即可。
六．应用题（共10小题）
38．【答案】见试题解答内容
【分析】根据利息＝本金×利率×存期，求出利息，然后用本金加上利息就是一共拿回的钱，据此列式解答．
【解答】解：1000+1000×3.5%×3
＝1000+1000×0.035×3
＝1000+105
＝1105（元）
答：期后淘气一共从银行拿回1105元．
【点评】这种类型属于利息问题，有固定的计算方法，利息＝本金×利率×存期，本息＝本金+利息，找清数据与问题，代入公式计算即可．
39．【答案】34棵。
【分析】用保护树的数量除以回收废纸的数量，求出每1t废纸相当于保护了多少棵树，再乘育人小学回收废纸的质量，即可求出育人小学回收的废纸进行再利用，相当于保护了多少棵树。
【解答】解：85÷5×2
＝17×2
＝34（棵）
答：相当于保护了34棵树。
【点评】本题主要考查了一位数除两位数除法的实际应用，先求出每1t废纸相当于保护了多少棵树是解答本题的关键。
40．【答案】见试题解答内容
【分析】先用65岁加上5岁，求出淘气年龄的5倍是多少，再除以5，即可求出淘气今年多少岁。
【解答】解：（65+5）÷5
＝70÷5
＝14（岁）
答：淘气今年14岁。
【点评】解决本题关键是理解倍数关系：已知一个数的几倍是多少，求这个数，用除法求解。
41．【答案】B木条，分别为4厘米和9厘米，5厘米和8厘米，6厘米和7厘米。
【分析】因为三角形的两边之和大于第三条边，两边之差小于第三条边，军应该锯断B木条，把B木条锯成两段，分别为4厘米和9厘米，5厘米和8厘米，6厘米和7厘米，根据三角形的两边之和大于第三条边，都可以和6厘米围成三角形，由此解答即可。
【解答】解：（1）锯断B木条，B木条可以和A木条围成三角形，因为三角形的两边之和大于第三条边。
（2）把B木条锯成两段，分别为4厘米和9厘米，5厘米和8厘米，6厘米和7厘米，根据三角形的两边之和大于第三条边，都可以和6厘米围成三角形
【点评】解答此题的关键是明确：三角形任意两边之和大于第三边，任意两边之差小于第三边。
42．【答案】见试题解答内容
【分析】观察第二个图发现：现在的总长度是原长方形的长度加上右边多出这部分的长度，多出的部分是原长方形的34比23长的部分，根据分数乘法的意义分别求出原长的34、23，再相减，得出右边多的长度，再加上原来一个长方形的长度即可。
【解答】解：19.2×34−19.2×23+19.2
＝14.4﹣12.8+19.2
＝1.6+19.2
＝20.8（厘米）
答：拼摆后的图形长20.8厘米。
【点评】解决本题关键是根据图二，得出现在的长度与原来长方形长的关系，从而解决问题。
43．【答案】7.85米。
【分析】通过观察图形可知，一面靠墙，用篱笆围成半圆形，需要篱笆的等于该圆周长的一半，根据圆的周长公式：C＝πd，把数据代入公式解答。
【解答】解：3.14×5÷2
＝15.7÷2
＝7.85（米）
答：建这个“畜禽饲养舍”需要7.85米长的篱笆。
【点评】此题主要考查圆的周长公式的灵活运用，关键是熟记公式。
44．【答案】见试题解答内容
【分析】①通过观察条形统计图可知：2022年我国人工智能企业中语音交互企业有10家，医疗企业有10家，所以薛亮的说法是正确的；另外机器人企业只有4家，安防领域有16家，根据求一个数是另一个数的几分之几得：机器人企业的家数是安防领域的4÷16=14，因此，李悦的说法是正确的；医疗企业有10家，安防领域有16家，求医疗企业比安防领域少百分之几，把安防领域的家数看作单位“1”，根据求一个数比另一个数，少百分之几，（16﹣10）÷16＝37.5%，因此王晶的说法是错误的．
②2022年我国人工智能企业中，AI领域发展最快，世界50强企业里我国从过去的8家增长到19家，在如此重要的高科技领域内中国取得如此的成就，也是吸引了世界的目光．所以中国最近在AI领域发展非常亮眼．
【解答】解：①2022年我国人工智能企业中语音交互企业有10家，医疗企业有10家，所以薛亮的说法是正确的；
另外机器人企业只有4家，安防领域有16家，根据求一个数是另一个数的几分之几得：机器人企业的家数是安防领域的4÷16=14，因此，李悦的说法是正确的；
医疗企业有10家，安防领域有16家，
（16﹣10）÷16
＝6÷16
＝0.375
＝37.5%，
所以，2022年我国人工智能企业中医疗企业比安防领域少37.5%．
因此王晶的说法是错误的．
所以，我不认同王晶同学的叙述．
②我觉得2022年我国人工智能企业中，AI领域发展最快，理由是：世界50强企业里我国从过去的8家增长到19家，在如此重要的高科技领域内中国取得如此的成就，也是吸引了世界的目光．所以中国最近在AI领域发展非常亮眼．
故答案为：王晶．
【点评】此题考查的目的是理解掌握条形统计图的特点及作用，并且能够根据统计图提供的信息，解决有关的实际问题．
45．【答案】见试题解答内容
【分析】（1）根据求平均数的方法，用这七天参观的总人数除以7即可．据此列式解答．
（2）把第七天参观的人数看作单位“1”，先求出第一天的参观人数比第七天多多少万人，再根据求一个数是另一个数的百分之几，用除法解答．
【解答】解：（1）（21+23+12.98+14.3+7.88+10.56+13.6）÷7
＝103.32÷7
＝14.76（万人）；
答：这7天平均每天的参观人数是14.76万人．

（2）（21﹣13.6）÷13.6
＝7.4÷13.6
≈0.54
＝54%；
答：第一天的参观人数比第七天多54%．
【点评】此题考查的目的是理解掌握折线统计图的特点及作用，并且能够根据统计图提供的信息，解决有关的实际问题．
46．【答案】见试题解答内容
【分析】根据题意：已知大杯的容积是小杯的2倍，则1个大杯的容积＝2个小杯的容积，即将1400mL果汁倒入3+2＝5个小杯中正好都倒满且无剩余，先求出小杯的容积，再求出大杯的容积．
【解答】解：1400÷（3+1×2）
＝1400÷5
＝280（毫升）
280×2＝560（毫升）
答：小杯的容积是280毫升，大杯的容积是560毫升．
【点评】解决此题的关键是应用等量代换即1个大杯的容积＝2个小杯的容积．
47．【答案】三轮车：6辆；自行车：12辆。
【分析】假设全是自行车，则有轮子的个数是18×2＝36个，这就与实际的轮子相差了42﹣36＝6个，这是因每辆三轮车比每辆自行车多了3﹣2＝1个轮子，就多出了6个轮子，据此可求出三轮车的辆数，再用18减，就是自行车的辆数。
【解答】解：三轮车的辆数：
（42﹣18×2）÷（3﹣2）
＝6÷1
＝6（辆）
自行车的辆数：
18﹣6＝12（辆）
答：三轮车有6辆，自行车有12辆。
【点评】此题属于鸡兔同笼问题，解这类题的关键是用假设法进行分析，进而得出结论；也可以用方程进行解答。