2023年广东省肇庆市高要区中考一模数学试题

2023年中考数学模拟试题（一）

注意：请在答题卡上作答．

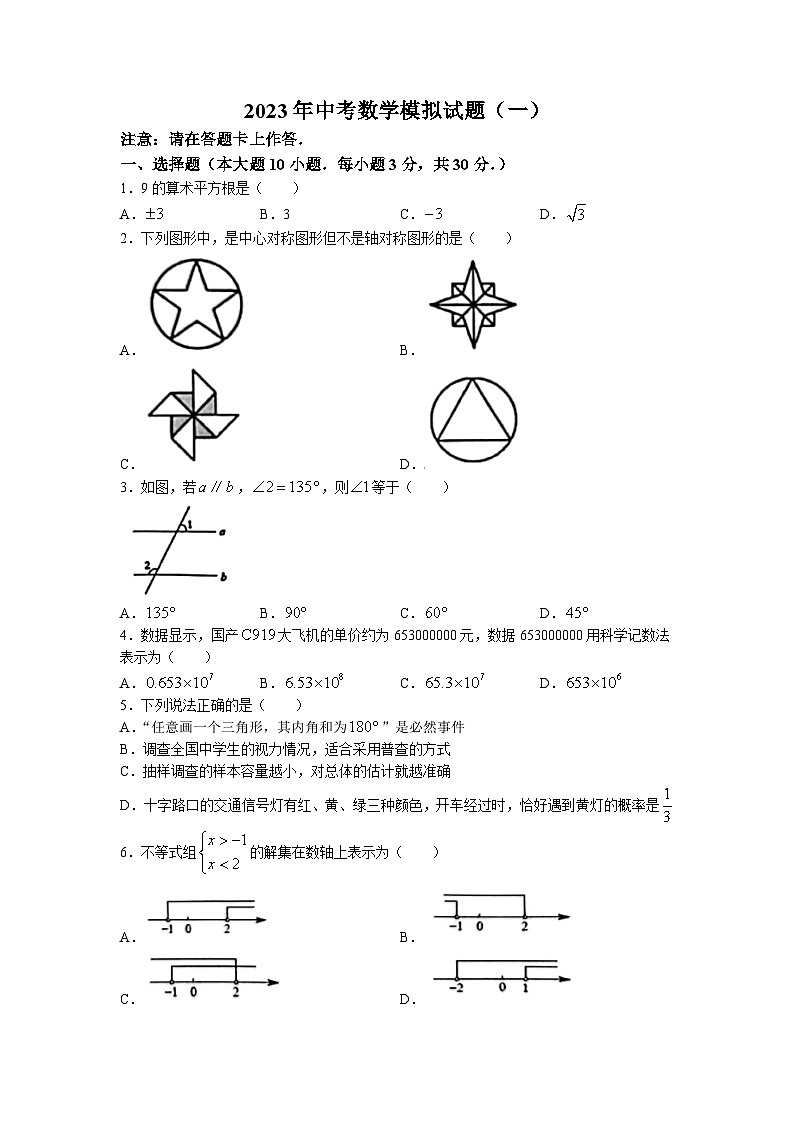
一、选择题（本大题10小题．每小题3分，共30分．）

1．9的算术平方根是（    ）

A． B．3 C． D．

2．下列图形中，是中心对称图形但不是轴对称图形的是（    ）

A．  B．

C．  D．

3．如图，若，，则等于（    ）

A． B． C． D．

4．数据显示，国产大飞机的单价约为653000000元，数据653000000用科学记数法表示为（    ）

A． B． C． D．

5．下列说法正确的是（    ）

A．“任意画一个三角形，其内角和为”是必然事件

B．调查全国中学生的视力情况，适合采用普查的方式

C．抽样调查的样本容量越小，对总体的估计就越准确

D．十字路口的交通信号灯有红、黄、绿三种颜色，开车经过时，恰好遇到黄灯的概率是

6．不等式组的解集在数轴上表示为（    ）

A． B．

C． D．

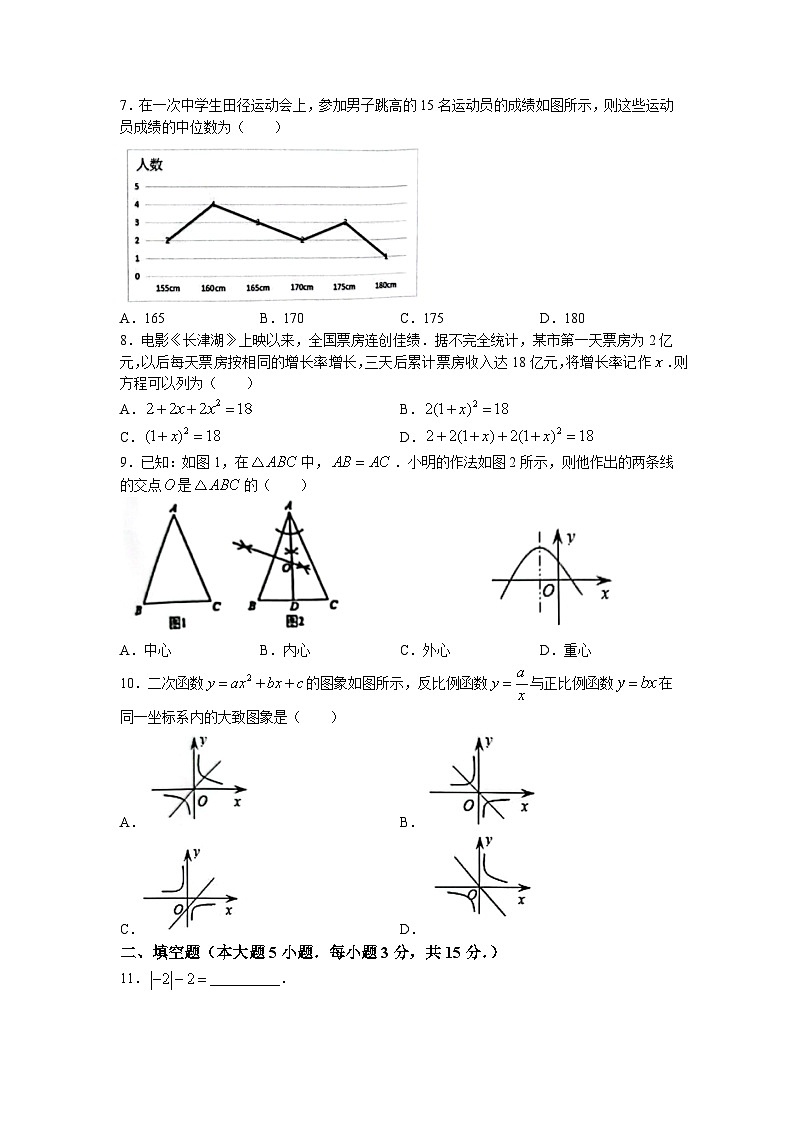
7．在一次中学生田径运动会上，参加男子跳高的15名运动员的成绩如图所示，则这些运动员成绩的中位数为（    ）

A．165 B．170 C．175 D．180

8．电影《长津湖》上映以来，全国票房连创佳绩．据不完全统计，某市第一天票房为2亿元，以后每天票房按相同的增长率增长，三天后累计票房收入达18亿元，将增长率记作．则方程可以列为（    ）

A．  B．

C．  D．

9．已知：如图1，在中，．小明的作法如图2所示，则他作出的两条线的交点是的（    ）

A．中心 B．内心 C．外心 D．重心

10．二次函数的图象如图所示，反比例函数与正比例函数在同一坐标系内的大致图象是（    ）

A．  B．

C．  D．

二、填空题（本大题5小题．每小题3分，共15分．）

11．__________．

12．若使分式有意义，则的取值范围是__________．

13．分解因式：__________．

14．如图，正方形中，点、分别在边、上，，，则__________度．

15．如图，在等腰中，，．分别以点，，为圆心，以的长为半径画弧分别与的边相交，则图中阴影部分的面积为__________．（结果保留）

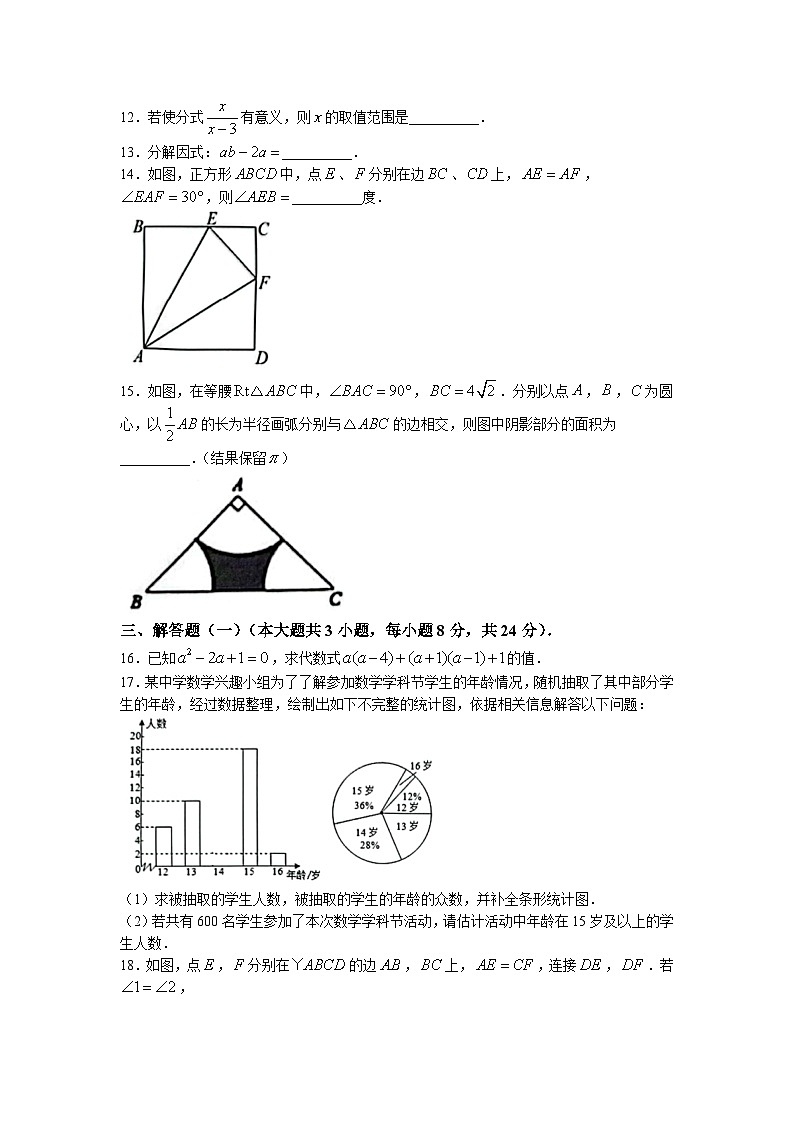
三、解答题（一）（本大题共3小题，每小题8分，共24分）．

16．已知，求代数式的值．

17．某中学数学兴趣小组为了了解参加数学学科节学生的年龄情况，随机抽取了其中部分学生的年龄，经过数据整理，绘制出如下不完整的统计图，依据相关信息解答以下问题：

（1）求被抽取的学生人数，被抽取的学生的年龄的众数，并补全条形统计图．

（2）若共有600名学生参加了本次数学学科节活动，请估计活动中年龄在15岁及以上的学生人数．

18．如图，点，分别在的边，上，，连接，．若，

（1）证明：．

（2）证明：为菱形．

四、解答题（二）（本大题共3小题．每小题9分，共27分）

19．某班组织学生参加全民健身线上跳绳活动，需购买，两种跳绳若干．若购买3根种跳绳和1根种跳绳共需140元；若购买5根种跳绳和3根种跳绳共需300元．

（1）求，两种跳绳的单价各是多少元？

（2）若该班准备购买，两种跳绳共46根，总费用不超过1780元，那么至多可以购买种跳绳多少根？

20．如图，矩形的边，分别与反比例函数的图象相交于点、，与相交于点．

（1）若点的坐标为，求点、、的坐标；

（2）求的长度．

21．2022年11月29日，搭载神舟十五号载人飞船的运载火箭在酒泉卫星发射中心成功发射．运载火箭从发射点处发射，当火箭到达处时、在地面雷达站处测得点的仰角为，在地面雷达站处测得点的仰角为．已知，、、三点在同一条直线上，求、两个雷达站之间的距离（结果精确到．参考数据）．

五、解答题（三）（本大题共2小题，每小题12分，共24分）．

22．如图，中，，平分，是上一点，以为直径作，若恰好经过点．

（1）求证：直线与相切；

（2）若,，求的半径的长．

23．如图，直线与轴、轴分别交于两点，抛物线经过、两点，且与轴交于点．

（1）求该抛物线的函数表达式；

（2）已知点是第一象限内抛物线上的一个动点，过点作平行于轴交直线于点，连接、、，求四边形面积的最大值，并求出此时点的坐标．

2023初中数学模拟1答案

一、选择题：BCDBA  CADCB

二、填空题：每题3分，共15分

11．0 12． 13． 14．30              15．

三、解答一（每题8分，共24分）

16．解：，，，

原式

17．解（1）由条形统计图可知，

被抽取的学生人数：（人），

被抽取的学生的年龄15岁最多，故众数是15岁；

14岁的学生有：（人），补全的条形统计图如图所示；

（2）16岁的学生有2（人），

（人），即估计活动中年龄在15岁及以上的学生有240人．

18．证明：（1）四边形为平行四边形，，

在和中，

，．

（2）由，得，为菱形．

四、解答二（每题9分，共27分）

19．解：（1）设种跳绳的单价为元，种跳绳的单价为元，

由题意得：，解得．

答：种跳绳的单价为30元，种跳绳的单价为50元．

（2）设购买种跳绳根，则购买种跳绳根，

由题意得：，解得，

答：至多可以购买种跳绳20根．

20．解：（1）点的坐标为，点横坐标为4，，点纵坐标为2，，

设直线的解析式为，，解得，

直线的解析式为，

直线的解析式为，联立方程组，

解得，；

（2），，由勾股定理得：．

21．解：在中，，，，

，，

在中，，，．

答：、两个雷达站之间的距离为．

五、解答三（每题12分，共24分）

22．（1）解：连结．

平分，．

又，．

，．

，，是的切线；

（2）连接，在中，，

，，，，

是的直径，，

，，，，

，的半径为．

23．解：（1）由得，，

令，得，，

由题意得：，解得，

抛物线解析式为．

（2）如图，设，，，

，

，当时，的最大值，此时点．