初中浙教版3.4 乘法公式精品同步练习题

专题3.4  乘法公式（专项训练）

1．（2022秋•广宗县期末）计算（0.1x+0.3y）（0.1x﹣0.3y）的结果为（　　）

A．0.01x2﹣0.09y2 B．0.01x2﹣0.9y2 

C．0.1x2﹣0.9y2 D．0.1x2﹣0.3y2

2．（2022•南京模拟）在下列计算中，不能用平方差公式计算的是（　　）

A．（x3﹣y3）（x3+y3） B．（c2﹣d2）（d2+c2） 

C．（﹣a﹣b）（a﹣b） D．（m﹣n）（﹣m+n）

3．（2022秋•龙亭区校级期末）已知a+b＝10，a﹣b＝6，则a2﹣b2的值是（　　）

A．12 B．60 C．﹣60 D．﹣12

4．（2022•鄞州区校级开学）下列各式不能用平方差公式计算的是（　　）

A．（5x﹣2ab）（5x+2ab） B．（x﹣y）（﹣x﹣y） 

C．（﹣ab﹣c）（ab﹣c） D．（m+n）（﹣m﹣n）

5．用简便方法计算107×93时，变形正确的是（　　）

A．1002﹣7 B．1002﹣72 

C．1002+2×100×7+72 D．1002﹣2×100×7+72

6．计算2022﹣201×203的结果是（　　）

A．1 B．﹣1 C．2 D．﹣2

7．（﹣5a2+4b2）（　　）＝25a4﹣16b4括号内应填 　   ．

8．（2022秋•河西区期末）计算：（x+3）（x﹣3）．

9．利用公式（平方差公式或完全平方公式）计算下列各题：

（1）97×103            （2）9982．

10．利用乘法公式计算：

（1）（﹣a+2）（﹣a﹣2）；              （2）1982．

11．（2022秋•邯山区期末）如图，从边长为a的大正方形中剪掉一个边长为b的小正方形，将阴影部分沿虚线剪开，拼成右边的矩形．根据图形的变化过程写出的一个正确的等式是（　　）

A．（a﹣b）2＝a2﹣2ab+b2 B．a（a﹣b）＝a﹣ab 

C．（a﹣b）2＝a2﹣b2 D．a2﹣b2＝（a+b）（a﹣b）

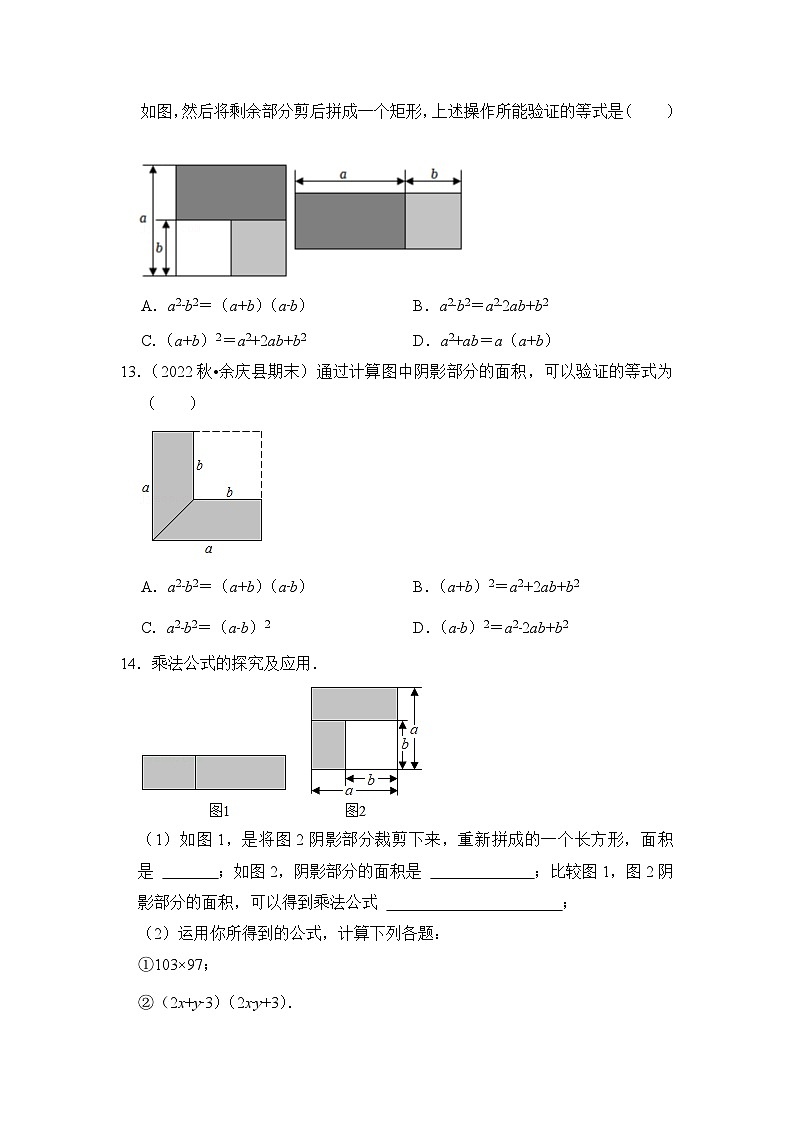
12．（2022秋•德州期末）从边长为a的正方形中去掉一个边长为b的小正方形，如图，然后将剩余部分剪后拼成一个矩形，上述操作所能验证的等式是（　　）

A．a2﹣b2＝（a+b）（a﹣b） B．a2﹣b2＝a2﹣2ab+b2 

C．（a+b）2＝a2+2ab+b2 D．a2+ab＝a（a+b）

13．（2022秋•余庆县期末）通过计算图中阴影部分的面积，可以验证的等式为（　　）

A．a2﹣b2＝（a+b）（a﹣b） B．（a+b）2＝a2+2ab+b2 

C．a2﹣b2＝（a﹣b）2 D．（a﹣b）2＝a2﹣2ab+b2

14．乘法公式的探究及应用．

（1）如图1，是将图2阴影部分裁剪下来，重新拼成的一个长方形，面积是 　   　；如图2，阴影部分的面积是              ；比较图1，图2阴影部分的面积，可以得到乘法公式 　                  　；

（2）运用你所得到的公式，计算下列各题：

①103×97；

②（2x+y﹣3）（2x﹣y+3）．

15．如图，从边长为a的正方形纸片中剪掉一个边长为b的正方形纸片（如图1），然后将剩余部分拼成一个长方形（如图2）．

（1）探究：上述操作能验证的等式是 　                   　．

（2）应用：利用（1）中得出的等式，计算：．

16．（2022秋•越秀区校级期末）计算（3x﹣1）2的结果是（　　）

A．6x2﹣6x+1 B．9x2﹣6x+1 C．9x2﹣6x﹣1 D．9x2+6x﹣1

17．（2022秋•卧龙区校级期末）（﹣m+1）2的计算结果为（　　）

A．1﹣m2 B．1﹣m+m2 C．m2+1 D．1+m+m2

18．（2022秋•东方期末）若x2+mxy+y2是一个完全平方式，那m的值是（　　）

A．±2 B．﹣2 C．±4 D．﹣4

19．（2022秋•丛台区校级期末）将1022变形正确的是（　　）

A．1022＝1002+22 B．1022＝（100+2）（100﹣2） 

C．1022＝1002+2×100×2+22 D．1022＝1002+100×2+22

20．（2022秋•东丽区期末）下列多项式是完全平方式的是（　　）

A．a2﹣4a+4 B．1+4a2 C．4b2+4b﹣1 D．a2+ab+b2

21．（2022秋•城关区校级期末）若a＝b+3，则a2﹣2ab+b2的值为（　　）

A．3 B．6 C．9 D．12

22．（2022秋•广宗县期末）小张利用如图①所示的长为a、宽为b的长方形卡片4张，拼成了如图②所示的图形，则根据图②的面积关系能验证的恒等式为（　　）

A．（a+b）2＝a2+2ab+b2 B．（2a+b）2＝4a2+4ab+b2 

C．（a+b）2＝（a﹣b）2+4ab D．（a﹣b）2＝a2﹣2ab+b2

23.（2022春•太原期中）通过两种不同的方法计算同一图形的面积可以得到一个数学等式，用这种方法可得到整式乘法中的一些运算法则或公式，例如，由图1可得等式（a+b）（c+d）＝ac+ad+bc+bd，即为多项式乘法法则．利用图2可得的乘法公式为（　　）

A．（a+b）2＝a2+b2 B．（a+b）2＝a2+2ab+b2 

C．（a+b）2＝a2+b2+ab D．（a+b）（a+b）＝a2+b2

24.（2022春•钢城区期末）美术课上，老师让同学们用彩色卡纸玩拼图的游戏，小芳同学拿着如图①所示的红色长方形卡纸，卡纸长为2a，宽为2b，她沿图中虚线平均分成四个小长方形，然后按照图②的方式拼成一个正方形，中间的空缺处（阴影部分）用黄色卡纸进行拼接．

（1）需要黄色卡纸的边长为                 ；

（2）请用两种不同的方法列代数式表示黄色卡纸的面积：

方法一 　                  　；

方法二 　                      　；

（3）观察图②直接写出（a+b）2，（a﹣b）2，ab这三个代数式之间的等量关系式 　    　；

（4）根据（3）中的等量关系解决下列问题：若a+b＝6，ab＝7，求（a﹣b）2的值．

25.（2022春•胶州市期中）阅读材料：

若x满足（9﹣x）（x﹣4）＝4，求（9﹣x）2+（x﹣4）2的值．

解：设9﹣x＝a，x﹣4＝b，则（9﹣x）（x﹣4）＝ab＝4，a+b＝（9﹣x）+（x﹣4）＝5，

∴（9﹣x）2+（x﹣4）2＝a2+b2＝（a+b）2﹣2ab＝52﹣2×4＝17．

类比应用：

请仿照上面的方法求解下列问题：

（1）若（3﹣x）（x﹣2）＝﹣1，求（3﹣x）2+（x﹣2）2的值；

（2）若（n﹣2021）2+（2022﹣n）2＝11，求（n﹣2021）（2022﹣n）的值；

（3）已知正方形ABCD的边长为x，E，F分别是AD，DC上的点，且AE＝1，CF＝3，长方形EMFD的面积是15．分别以MF，DF为边长作正方形MFRN和正方形GFDH，求正方形MFRN和正方形GFDH的面积和．

26．（2022秋•孝昌县期末）若a﹣b＝5，a2+b2＝13，则ab＝　  　．

27．（2022秋•黄陂区期末）已知a2+b2＝17，ab＝4，则（a+b）2的值是 　 　．

28．（2022•大庆二模）已知x+y＝4，xy＝3，求x2+y2的值．

29．（2022春•新邵县期中）已知：a2+ab＝15，b2+ab＝10，a﹣b＝1，求下列各式的值：

（1）a+b的值；

（2）a2+b2的值．