



专题23函数与矩形存在性问题-中考数学压轴大题之经典模型培优案(全国通用)
展开中考数学压轴大题之经典模型培优案
专题23函数与矩形存在性问题
解题策略
1.矩形的判定:
(1)有一个角是直角的平行四边形是矩形;
(2)对角线相等的平行四边形是矩形;
(3)有三个角为直角的四边形是矩形.
2.题型分析
矩形除了具有平行四边形的性质之外,还有“对角线相等”或“一个角为直角”,因此相比起平行四边形,坐标系中的矩形满足以下3个等式:
因此在矩形存在性问题最多可以有3个未知量,代入可以得到三元一次方程组,可解.
确定了有3个未知量,则可判断常见矩形存在性问题至少有2个动点,多则可以有3个.下:
同时,也可以先根据A、B的坐标求出直线AB的解析式,进而得到直线AD或BC的解析式,从而确定C或D的坐标.
经典例题
【例1】(2022春•宾阳县期中)在四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=24cm,BC=26cm.点P从点A出发,以1cm/s的速度向点D运动,点Q从点C出发,以3cm/s的速度向点B同时运动.规定其中一个动点到达端点时,另一个动点也随之停止运动.设P,Q运动的时间为ts.
(1)若点P和点Q同时运动了6秒,PQ与CD有什么数量关系?并说明理由;
(2)在整个运动过程中是否存在t值,使得四边形PQBA是矩形?若存在,请求出t值;若不存在,请说明理由;
(3)在整个运动过程中,是否存在一个时间,使得四边形PQBA的面积是四边形ABCD面积的一半,若存在,请直接写出值;若不存在,请说明理由.
【分析】(1)根据t=6可得PD=CQ,从而得出四边形PDCQ为平行四边形,即可得出PQ=CD;
(2)当AP=BQ时,四边形ABQP是矩形,得t=26﹣3t,即可解决问题;
(3)根据梯形的面积公式分别表示出四边形ABCD和PQBA的面积,列出方程,进而解决问题.
【解答】解:(1)PQ=CD,理由如下:
由题意得:AP=tcm,CQ=3tcm,
∵AB=8cm,AD=24cm,BC=26cm,
∴AP=(24﹣t)cm,
当t=6时,DP=18cm,CQ=18cm,
∴DP=CQ,
∵DP∥CQ,
∴四边形PDCQ是平行四边形,
∴PQ=CD;
(2)在四边形ABCD中,AD∥BC,∠B=90°,
∴当AP=BQ时,四边形ABQP是矩形,
∴t=26﹣3t,
解得t=6.5,
∴当t=6.5时,四边形ABQP是矩形;
(3)存在,由题意知,四边形ABCD的面积==,
四边形PQBA的面积==4(t+26﹣3t)=104﹣8t,
∵四边形PQBA的面积是四边形ABCD面积的一半,
∴104﹣8t=100,
∴t=.
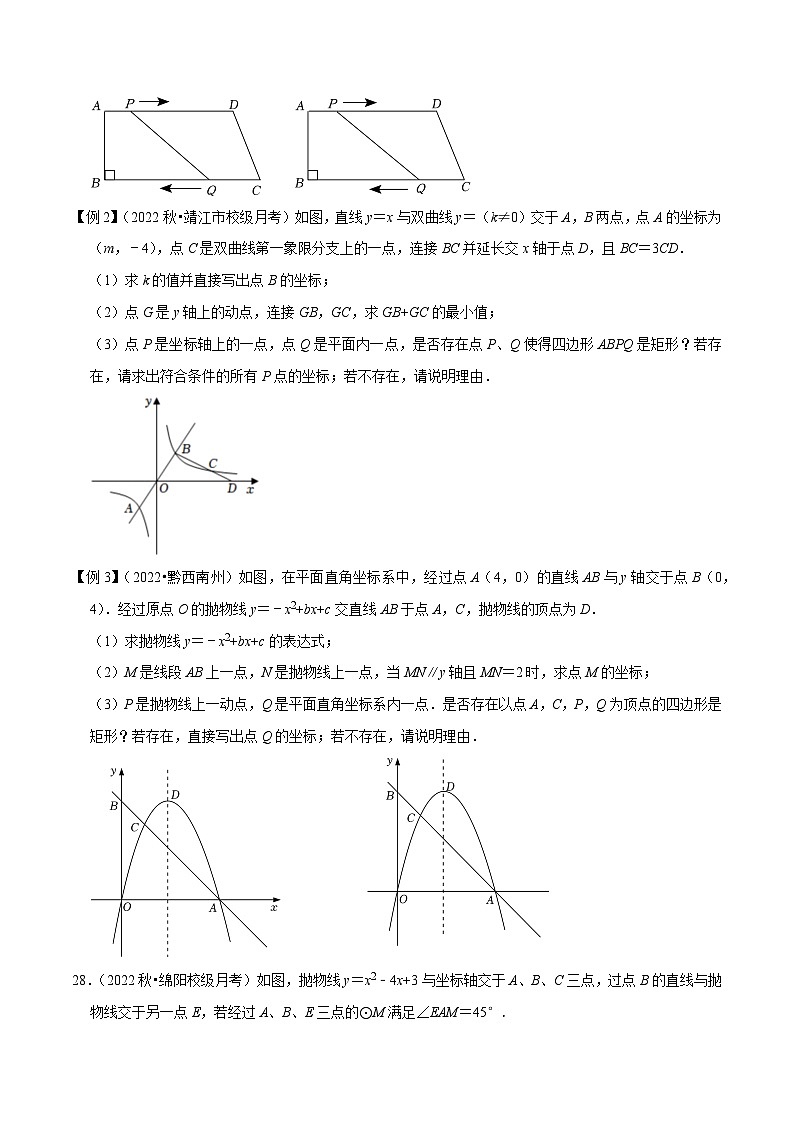
【例2】(2022秋•靖江市校级月考)如图,直线y=x与双曲线y=(k≠0)交于A,B两点,点A的坐标为(m,﹣4),点C是双曲线第一象限分支上的一点,连接BC并延长交x轴于点D,且BC=3CD.
(1)求k的值并直接写出点B的坐标;
(2)点G是y轴上的动点,连接GB,GC,求GB+GC的最小值;
(3)点P是坐标轴上的一点,点Q是平面内一点,是否存在点P、Q使得四边形ABPQ是矩形?若存在,请求出符合条件的所有P点的坐标;若不存在,请说明理由.
【分析】(1)将点A的坐标为(m,﹣4)代入直线y=x中,可求得A(﹣3,﹣4),即可求得k=12,根据轴对称的性质即可求出点B的坐标;
(2)如图1,作BE⊥x轴于点E,CF⊥x轴于点F,则BE∥CF,△DCF∽△DBE,利用相似三角形性质即可求得C(12,1),作点B关于y轴的对称点B′,连接B′C交y轴于点G,则B′C即为BG+GC的最小值,运用勾股定理即可求得答案;
(3)分两种情况:①当点P在x轴上时,如图2,设点P1的坐标为(a,0),过点B作BE⊥x轴于点E,通过△OBE∽△OP1B,建立方程求解即可;
②当点P在y轴上时,过点B作BN⊥y轴于点N,如图2,设点P2的坐标为(0,b),利用△BON∽△P2OB,建立方程求解即可.
【解答】解:(1)∵A(m,﹣4)在直线y=x上,
∴m=﹣4,
解得m=﹣3,
∴A(﹣3,﹣4),
∵A(﹣3,﹣4)在y=上,
∴k=12,
∴y=,
∵直线y=x与双曲线y=(k≠0),
∴A、B关于原点对称,
∴B(3,4);
(2)如图1,作BE⊥x轴于点E,CF⊥x轴于点F,
∴BE∥CF,
∴△DCF∽△DBE,
∴=,
∵BC=3CD,BE=4,
∴=,
∴=,
∴CF=1,
∴C(12,1),
作点B关于y轴的对称点B′,连接B′C交y轴于点G,
则B′C即为BG+GC的最小值,
∵B′(﹣3,4),C(12,1),
∴B′C==3,
∴BG+GC=B′C=3;
故GB+GC的最小值为3;
(3)(3)存在.理由如下:
①当点P在x轴上时,如图2,设点P1的坐标为(a,0),
过点B作BE⊥x轴于点E,
∵∠OEB=∠OBP1=90°,∠BOE=∠P1OB,
∴△OBE∽△OP1B,
∴=,
∵B(3,4),
∴OB==5,
∴=,
∴a=,
∴点P1的坐标为(,0);
②当点P在y轴上时,过点B作BN⊥y轴于点N,如图2,
设点P2的坐标为(0,b),
∵∠ONB=∠P2BO=90°,∠BON=∠P2OB,
∴△BON∽△P2OB,
∴=,即=,
∴b=,
∴点P2的坐标为(0,);
综上所述,点P的坐标为(,0)或(0,).
【例3】(2022•黔西南州)如图,在平面直角坐标系中,经过点A(4,0)的直线AB与y轴交于点B(0,4).经过原点O的抛物线y=﹣x2+bx+c交直线AB于点A,C,抛物线的顶点为D.
(1)求抛物线y=﹣x2+bx+c的表达式;
(2)M是线段AB上一点,N是抛物线上一点,当MN∥y轴且MN=2时,求点M的坐标;
(3)P是抛物线上一动点,Q是平面直角坐标系内一点.是否存在以点A,C,P,Q为顶点的四边形是矩形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
【分析】(1)将点A、O的坐标分别代入抛物线解析式,解方程即可;
(2)设直线AB的解析式为y=kx+b,利用待定系数法求出解析式,再表示出MN,然后根据MN=2解方程可得答案;
(3)分AC为边和对角线两种情况进行讨论:根据平移的性质,三角形相似的性质和判定,两点的距离公式可得结论.
【解答】解:(1)∵抛物线y=﹣x2+bx+c过点A(4,0)和O(0,0),
∴,
解得:,
∴抛物线的解析式为:y=﹣x2+4x;
(2)∵直线AB经过点A(4,0)和B(0,4),
∴直线AB的解析式为:y=﹣x+4,
∵MN∥y轴,
设M(t,﹣t+4),N(t,﹣t2+4t),其中0≤t≤4,
当M在N点的上方时,
MN=﹣t+4﹣(﹣t2+4t)=t2﹣5t+4=2,
解得:t1=,t2=(舍),
∴M1(,),
当M在N点下方时,
MN=﹣t2+4t﹣(﹣t+4)=﹣t2+5t﹣4=2,
解得:t1=2,t2=3,
∴M2(2,2),M3(3,1),
综上,满足条件的点M的坐标有三个(,)或(2,2)或(3,1);
(3)存在,
①如图2,若AC是矩形的边,
设抛物线的对称轴与直线AB交于点R,且R(2,2),
过点C,A分别作直线AB的垂线交抛物线于点P1,P2,
∵C(1,3),D(2,4),
∴CD==,
同理得:CR=,RD=2,
∴CD2+CR2=DR2,
∴∠RCD=90°,
∴点P1与点D重合,
当CP1∥AQ1,CP1=AQ1时,四边形ACP1Q1是矩形,
∵C(1,3)向右平移1个单位,向上平移1个单位得到P1(2,4),
∴A(4,0)向右平移1个单位,向上平移1个单位得到Q1(5,1),
此时直线P1C的解析式为:y=x+2,
∵直线P2A与P1C平行且过点A(4,0),
∴直线P2A的解析式为:y=x﹣4,
∵点P2是直线y=x﹣4与抛物线y=﹣x2+4x的交点,
∴﹣x2+4x=x﹣4,
解得:x1=﹣1,x2=4(舍),
∴P2(﹣1,﹣5),
当AC∥P2Q2时,四边形ACQ2P2是矩形,
∵A(4,0)向左平移3个单位,向上平移3个单位得到C(1,3),
∴P2(﹣1,﹣5)向左平移3个单位,向上平移3个单位得到Q2(﹣4,﹣2);
②如图3,若AC是矩形的对角线,
设P3(m,﹣m2+4m)
当∠AP3C=90°时,过点P3作P3H⊥x轴于H,过点C作CK⊥P3H于K,
∴∠P3KC=∠AHP3=90°,∠P3CK=∠AP3H,
∴△P3CK∽△AP3H,
∴=,
∴=,
∵点P不与点A,C重合,
∴m≠1或m≠4,
∴﹣m2﹣3m+1=0,
∴m=,
∴如图4,满足条件的点P有两个,即P3(,),P4(,),
当P3C∥AQ3,P3C=AQ3时,四边形AP3CQ3是矩形,
∵P3(,)向左平移个单位,向下平移个单位得到C(1,3),
∴A(4,0)向左平移个单位,向下平移个单位得到Q3(,),
当P4C∥AQ4,P4C=AQ4时,四边形AP4CQ4是矩形,
∵P4(,)向右平移个单位,向上平移个单位得到C(1,3),
∴A(4,0)向右平移个单位,向上平移个单位得到Q4(,);
综上,点Q的坐标为(5,1)或(﹣4,﹣2)或(,)或(,).
【例4】(2022秋•绵阳校级月考)如图,抛物线y=x2﹣4x+3与坐标轴交于A、B、C三点,过点B的直线与抛物线交于另一点E,若经过A、B、E三点的⊙M满足∠EAM=45°.
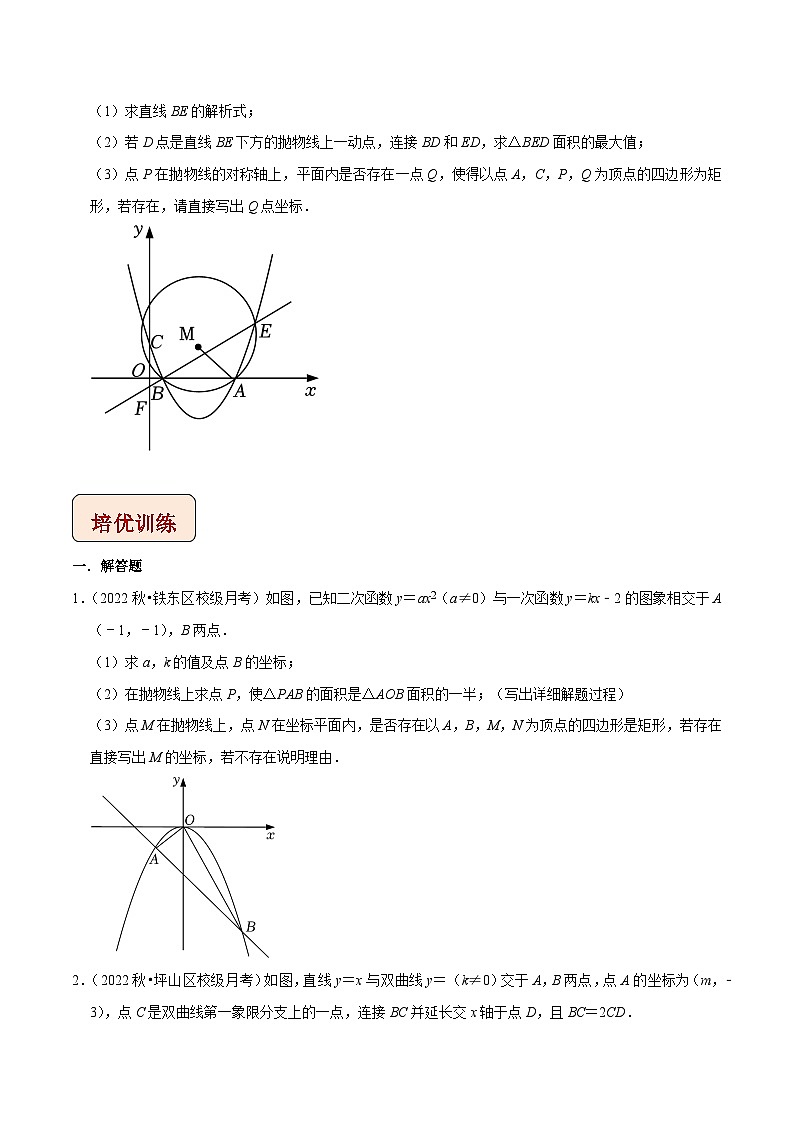
(1)求直线BE的解析式;
(2)若D点是直线BE下方的抛物线上一动点,连接BD和ED,求△BED面积的最大值;
(3)点P在抛物线的对称轴上,平面内是否存在一点Q,使得以点A,C,P,Q为顶点的四边形为矩形,若存在,请直接写出Q点坐标.
【分析】(1)设线段BC的垂直平分线与抛物线的对称轴交于点M,设M(2,a),想办法求出点M的坐标,再证明△MBC是等腰直角三角形,再作点C关于直线x=2的对称点E(4,3),根据对称性可知:∠EAM=45°,最后利用待定系数法即可解决问题.
(2)过点D作DM∥y轴交BE于点M,设点D(m,m2﹣4m+3),则N(m,m﹣1),根据三角形的面积公式可得出结论;
(3)根据对角线的情况分三种讨论,再由矩形的性质求出点Q的坐标.
【解答】解:(1)令y=0,则x2﹣4x+3=0,
解得x1=1,x2=3,
∴点A(3,0),B(1,0),
令x=0,则y=3,
∴点C(0,3),
设线段BC的垂直平分线与抛物线的对称轴交于点M,设M(2,a),
∵MB=MC,
∴(2﹣1)2+a2=22+(3﹣a)2,
解得a=2,
∴点M(2,2),
∵BC=,MC=,BM=,
∴BC2=MC2+BM2,
∴∠CMB=90°,
∵MC=MB,
∴△MCB是等腰直角三角形,
∴∠MBC=45°,
作点C关于直线x=2的对称点E,则E(4,3)在抛物线上,
根据对称性可知:∠EAM=∠MBC=45°
设直线BE的解析式为y=kx+b(k≠0),
则,
解得,
∴直线BE的解析式为y=x﹣1.
(2)如图,过点D作DN∥y轴交BE于点N,
设点D(m,m2﹣4m+3),则N(m,m﹣1),
∴S△BDE=×(xE﹣xB)×|DN|
=×3×[m﹣1﹣(m2﹣4m+3)]
=﹣(m﹣)2+,
∴当m=时,S△BDE取最大值;此时D(,﹣);
(3)存在,理由如下:
根据轴对称的公式可知,x=2,
∴设P(2,y),Q(m,n),
由(1)知A(3,0),C(0,3),
∴AC=3,AP2=12+y2,CP2=22+(y﹣3)2,
若AP为矩形的对角线,
由中点坐标公式得,
解得,
∴Q(5,y﹣3),
又∵∠ACP=90°,
∴AC2+CP2=AP2,
即:18+22+(y﹣3)2=12+y2,
解得y=5,
∴Q(5,2),
若CP为矩形的对角线,
由中点坐标公式得,
解得:,
∴Q(﹣1,y+3),
又∵∠CAP=90°,
∴AC2+AP2=CP2,
即:18+12+y2=22+(y﹣3)2,
解得y=﹣1,
∴Q(﹣1,2),
若AC为矩形的对角线,
由中点坐标公式得,
解得,
又∵∠APC=90°,
∴AP2+CP2=AC2,
即:12+y2+22+(y﹣3)2=18,
解得y=+或y=,
∴Q(1,+)或Q(1,﹣).
综上,点Q的坐标为(5,2)或(﹣1,2)或(1,+)或(1,﹣).
培优训练
一.解答题
1.(2022秋•铁东区校级月考)如图,已知二次函数y=ax2(a≠0)与一次函数y=kx﹣2的图象相交于A(﹣1,﹣1),B两点.
(1)求a,k的值及点B的坐标;
(2)在抛物线上求点P,使△PAB的面积是△AOB面积的一半;(写出详细解题过程)
(3)点M在抛物线上,点N在坐标平面内,是否存在以A,B,M,N为顶点的四边形是矩形,若存在直接写出M的坐标,若不存在说明理由.
【分析】(1)根据待定系数法即可求得,联立解析式,解方程组即可求得B的坐标;
(2)设直线AB交y轴于C,取OC的中点D,在OC的延长线截取CE=CD,作DM∥AB,交抛物线于P1,P2,作CN∥AB,交抛物线于P3,P4,求出DM和CE的解析式,进而和抛物线联立,进一步求得结果;
(3)分为矩形AMNB、矩形ABMN、矩形AMBN(M在直线AB上方和下方的抛物线上).当矩形AMNB时,点M和点O重合;当矩形ABMN时,作BC∥y轴,作AC⊥BC于C,作MD⊥BC于D,可证得△BDM是等腰直角三角形,进一步求得点M的坐标,当矩形AMBN,点M在AB上方的抛物线上时,作MC∥x轴,作AC⊥MC于C,作BD⊥MC于D,可得△BDM∽△MCA,从而,即=,进而求得m的值,进一步得出结果.
【解答】解:(1)∵y=ax2过点A(﹣1,﹣1),
∴﹣1=a×1,解得a=﹣1,
∵一次函数y=kx﹣2的图象相过点A(﹣1,﹣1),
∴﹣1=﹣k﹣2,解得k=﹣1;
解得或,
∴B的坐标为(2,﹣4);
(2)如图1,
设直线AB交y轴于C,取OC的中点D,在OC的延长线截取CE=CD,作DM∥AB,交抛物线于P1,P2,作CN∥AB,交抛物线于P3,P4,
∴△ODP1∽△OCA,
∴=,
∴=S△AOB,
∵C(0,﹣2,),
∴D(0,﹣1),E(0,﹣3),
∴直线DM的解析式为y=x﹣1,
由得,
,,
∴点P1(,)或P2(,);
同理可得,
点P3(,)或P4(,);
综上所述,点P(,)或(,)或(,)或(,);
(3)当矩形MABN是矩形时,∠MAB=90°,
由﹣x2=﹣x﹣2得,
x1=﹣1,x2=2,
∴B(2,﹣4),
∴OB2=20,
∵A(﹣1,﹣1),
∴AB2=18,OA2=2,
∴AB2+OA2=OB2,
∴∠OAB=90°,
∴点M和点O重合,
∴M(0,0),
如图2,
当矩形ABMN时,∠ABM=90°,
作BC∥y轴,作AC⊥BC于C,作MD⊥BC于D,
∵AC=BC=3,
∴△ABC是等腰直角三角形,
∴△BDM是等腰直角三角形,
∴DM=BD,
设M(m,﹣m2),
∴BD=﹣4+m2,DM=2﹣m,
∴﹣4+m2=2﹣m,
∴m1=2,m2=﹣3,
∴M(﹣3,﹣9),
如图3,
当点M在AB上方的抛物线上时,当∠AMB=90° 时,
作MC∥x轴,作AC⊥MC于C,作BD⊥MC于D,
同理可得:△BDM∽△MCA,
∴,
∴=,
∴m=,
当m=时,y=,
∴M(,),
当m=,y=﹣,
∴M(,﹣),
如图4,
当点M在AB下方的抛物线上,当∠AMB=90°时,
同理可得,
=,
∴m=,
当m=时,y=,
∴M(,),
当m=时,y=﹣,
∴M(,﹣),
综上所述:M(0,0)或(﹣3,﹣9)或(,)或(,﹣)或(,)或(,﹣).
2.(2022秋•坪山区校级月考)如图,直线y=x与双曲线y=(k≠0)交于A,B两点,点A的坐标为(m,﹣3),点C是双曲线第一象限分支上的一点,连接BC并延长交x轴于点D,且BC=2CD.
(1)求k的值并直接写出点B的坐标;
(2)点G是y轴上的动点,连接GB,GC,求GB+GC的最小值;
(3)P是x轴上的点,Q是平面内一点,是否存在点P,Q,使得A,B,P,Q为顶点的四边形是矩形?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
【分析】(1)将点A的坐标为(m,﹣3)代入直线y=x中,可求得A(﹣2,﹣3),即可求得k=6,解方程组,即可求出点B的坐标;
(2)如图1,作BE⊥x轴于点E,CF⊥x轴于点F,则BE∥CF,△DCF∽△DBE,利用相似三角形性质即可求得C(6,1),作点B关于y轴的对称点B′,连接B′C交y轴于点G,则B′C即为BG+GC的最小值,运用勾股定理即可求得答案;
(3)分两种情况:当点P在x的正半轴上时,当点P在x的负轴上时,如图2,设点P1的坐标为(a,0),过点B作BE⊥x轴于点E,通过△OBE∽△OP1B,建立方程求解即可.
【解答】解:(1)将点A的坐标为(m,﹣3)代入直线y=x中,
得﹣3=m,
解得:m=﹣2,
∴A(﹣2,﹣3),
∴k=﹣2×(﹣3)=6,
∴反比例函数解析式为y=,
由,得或,
∴点B的坐标为(2,3);
(2)如图1,作BE⊥x轴于点E,CF⊥x轴于点F,
∴BE∥CF,
∴△DCF∽△DBE,
∴=,
∵BC=2CD,BE=3,
∴=,
∴=,
∴CF=1,
∴C(6,1),
作点B关于y轴的对称点B′,连接B′C交y轴于点G,
则B′C即为BG+GC的最小值,
∵B′(﹣2,3),C(6,1),
∴B′C==2,
∴BG+GC=B′C=2;
(3)存在.理由如下:
当点P在x的正半轴上时,如图2,设点P1的坐标为(a,0),
过点B作BE⊥x轴于点E,
∵∠OEB=∠OBP1=90°,∠BOE=∠P1OB,
∴△OBE∽△OP1B,
∴=,
∵B(2,3),
∴OB==,
∴=,
∴a=,
∴点P1的坐标为(,0),
当点P在x的负轴上时,如图2,设点P2的坐标为(a,0),
过点A作AH⊥x轴于点H,
同理证得点P2的坐标为(﹣,0),
当四边形AP3BQ3或是矩形四边形AP4BQ4时,OA=OP4=,
∴点P的坐标为(﹣,0)或(,0),
综上所述,点P的坐标为(,0)或(﹣,0)或(﹣,0)或(,0).
3.(2022•锦州二模)如图,在平面直角坐标系中,矩形OABC的两边OA,OC分别在x轴和y轴上,OA=3,OC=4,抛物线y=ax2+bx+4经过点B,且与x轴交于点D(﹣1,0)和点E.
(1)求抛物线的表达式;
(2)若P是第一象限抛物线上的一个动点,连接CP,PE,当四边形OCPE的面积最大时,求点P的坐标,此时四边形OCPE的最大面积是多少;
(3)若N是抛物线对称轴上一点,在平面内是否存在一点M,使以点C,D,M,N为顶点的四边形是矩形?若存在,请直接写出点M的坐标;若不存在,说明理由.
【分析】(1)利用矩形的性质结合OA,OC的长度可得出点A,C,B的坐标,再利用待定系数法即可求出抛物线的表达式;
(2)利用二次函数图象上点的坐标特征,可求出点E的坐标,过点P作PF⊥x轴于点F,设点P的坐标为(m,﹣m2+3m+4)(0<m<4),利用S四边形OCPE=S梯形OCPF+S△APE,即可得出S四边形OCPE关于m的函数关系式,再利用二次函数的性质,即可求出结论;
(3)利用二次函数的性质,可得出抛物线对称轴为直线直线x=,利用待定系数法可求出直线CD的表达式,分CD为边及CD为对角线两种情况考虑:①当CD为边时,利用CN⊥CD或DN⊥CD可得出CN或DN的表达式,利用一次函数图象上点的坐标特征可得出点N的坐标,再利用矩形的性质即可求出点M的坐标;②当CD为对角线时,设线段CD的中点为G,过点G作GH⊥抛物线对称轴于点H,利用勾股定理可求出HN的长度,进而可得出点N的坐标,再利用矩形的性质即可求出点M的坐标.
【解答】解:(1)∵四边形OABC为矩形,且OA=3,OC=4,
∴点A的坐标为(3,0),点C的坐标为(0,4),点B的坐标为(3,4).
将B(3,4),D(﹣1,0)代入y=ax2+bx+4,
得:,解得:,
∴抛物线的表达式为y=﹣x2+3x+4.
(2)当y=0时,﹣x2+3x+4=0,
解得:x1=﹣1,x2=4,
∴点E的坐标为(4,0),
∴OE=4.
过点P作PF⊥x轴于点F,如图1所示.
设点P的坐标为(m,﹣m2+3m+4)(0<m<4),
则S四边形OCPE=S梯形OCPF+S△APE
=(OC+PF)•OF+FE•PF
=(4﹣m2+3m+4)•m+(4﹣m)•(﹣m2+3m+4)
=﹣2m2+8m+8
=﹣2(m﹣2)2+16,
∵﹣2<0,
∴m=2时,S四边形OCPE取得最大值,最大值=16,此时点P的坐标为(2,6),
∴当四边形OCPE的面积最大时,点P的坐标为(2,6),此时四边形OCPE的最大面积是16.
(3)∵抛物线的表达式为y=﹣x2+3x+4,
∴抛物线的对称轴为直线x=.
利用待定系数法可求出直线CD的表达式为y=4x+4,分CD为边及CD为对角线两种情况考虑:
①当CD为边时,若四边形DCNM为矩形,则直线CN的解析式为y=﹣x+4,
∴点N的坐标为(,),
∴点M的坐标为(﹣1+﹣0,0+﹣4),即(,﹣);
若四边形CDNM为矩形,则直线DN的解析式为y=﹣x﹣,
∴点N的坐标为(,﹣),
∴点M的坐标为(0+﹣(﹣1),4﹣﹣0),即(,);
②当CD为对角线时,设线段CD的中点为G,过点G作GH⊥抛物线对称轴于点H,如图3所示.
∵点C的坐标为(0,4),点D的坐标为(﹣1,0),
∴点G的坐标为(﹣,2),
∴点H的坐标为(,2),
∴GH=﹣(﹣)=2.
又∵以点C,D,M,N为顶点的四边形是矩形,即△OCN为直角三角形,
∴GN=OC==,
∴HN===,
∴点N的坐标为(,)或(,).
当点N的坐标为(,)时,点M的坐标为(﹣1+0﹣,0+4﹣),即(﹣,);
当点N的坐标为(,)时,点M的坐标为(﹣1+0﹣,0+4﹣),即(﹣,).
综上所述,在平面内存在一点M,使以点C,D,M,N为顶点的四边形是矩形,点M的坐标为(,﹣)或(,)或(﹣,)或(﹣,).
4.(2022•铁锋区三模)综合与探究
已知:如图,二次函数y=ax2+bx+c的图象的顶点为D(﹣1,4),与x轴交于B,A两点,与y轴交于点C(0,3),点E为抛物线对称轴上的一个动点.
(1)求二次函数的解析式;
(2)当△ACE的周长最小时,点E的坐标为 (﹣1,2) ;
(3)当点E在x轴上方且∠BAE=∠BDE时,试判断CE与BD的位置关系,并说明理由;
(4)若点N是y轴上的一点,坐标平面内是否存在P,使以D、B、N、P为顶点的四边形为矩形?若存在,请直接写出满足条件的点P的坐标;若不存在,请说明理由.
【分析】(1)设二次函数的解析式为顶点式,将点C坐标代入,进一步求得结果;
(2)点A关于对称轴的对称点时B,所以连接BC交对称轴于E,可求得BC的解析式,将x=﹣1代入求得点E的纵坐标,从而得出结果;
(3)可根据tan∠BAE=tan∠BDE得出,从而求得EF,进而求得CE和BD的解析式,从而得出结果;
(4)分为BD是边和对角线两种情形.当BD为边时,可根据相似三角形或三角函数关系式得出ON,从而得出N点的坐标,进而求得P点坐标;当BD为对角线时,利用对角线互相平分且相等,列出方程,求得N的坐标,进而得出点P坐标.
【解答】解:(1)设y=a(x+1)2+4,
把x=0,y=3代入得,
a+4=3,
∴a=﹣1,
∴y=﹣(x+1)2+4;
(2)连接BC,交对称轴于E,此时△ACE的周长最小,
由﹣(x+1)2=4得,
x=1或x=﹣3,
∴B(﹣3,0),
∴直线BC的解析式为:y=x+3,
∴当x=﹣1时,y=﹣1+3=2,
∴点E(﹣1,2),
故答案为:(﹣1,2);
(3)如图1,
∵∠BAE=∠BDE,
∴tan∠BAE=tan∠BDE,
∴,
∴,
∴EF=1,
∴E(﹣1,1),
∵C(0,3),
∴直线CE的解析式为:y=2x+3,
∵B(﹣3,0),D(﹣1,4),
∴直线BD的解析式为:y=2x+6,
∴BD∥CE;
(4)如图2,
存在点P,是以D、B、N、P为顶点的四边形是矩形:
当矩形DBNP时,(图中矩形DBN1P2),
可得tan∠N1BO=tan∠BDF,
∴,
∴ON1=,
∴N1(0,﹣),
∴P1(2,);
当矩形BDN2P2时,
同理可得:N2(0,),
∴P2(﹣2,﹣),
当矩形BNDP时,
可知BD的中点坐标为:(﹣2,2),
设点N(0,m),
由PN=BD得,
22+(m﹣2)2=()2,
∴m=1或m=3,
∴N3(0,1),则P3(﹣4,3),
N4(0,3),则P4(﹣4,1),
综上所述:P(2,)或(﹣2,﹣)或(﹣4,3)或(﹣4,1).
5.(2022•齐齐哈尔三模)综合与实践
如图,二次函数y=﹣x2+c的图象交x轴于点A、点B,其中点B的坐标为(2,0),点C的坐标为(0,2),过点A、C的直线交二次函数的图象于点D.
(1)求二次函数和直线AC的函数表达式;
(2)连接DB,则△DAB的面积为 6 ;
(3)在y轴上确定点Q,使得∠AQB=135°,点Q的坐标为 (0,2﹣2)或(0,2﹣2) ;
(4)点M是抛物线上一点,点N为平面上一点,是否存在这样的点N,使得以点A、点D、点M、点N为顶点的四边形是以AD为边的矩形?若存在,请你直接写出点N的坐标;若不存在,请说明理由.
【分析】(1)利用待定系数法可求出c的值,进而可得出二次函数的表达式,利用二次函数图象上点的坐标特征可求出点A的坐标,再由点A,C的坐标,利用待定系数法即可求出直线AC的函数表达式;
(2)联立直线AC和抛物线的函数表达式可求出点D的坐标,再结合点A,B的坐标,利用三角形的面积计算公式,即可求出△DAB的面积;
(3)当点Q在y轴正半轴轴时,过点Q作QE⊥AC于点E,根据各角之间的关系可得出AQ平分∠OAC,利用角平分线的性质及面积法,可求出OQ的长,进而可得出点Q的坐标;当点Q在y轴负半轴时,利用对称性可得出点Q的坐标;
(4)连接BC,则AD⊥BC,分四边形ADMN为矩形及四边形ADNM为矩形两种情况考虑:①当四边形ADMN为矩形时,利用平行线的性质及待定系数法可求出直线DM的函数表达式,联立后可求出点M的坐标,再利用矩形的性质可求出点N的坐标;②当四边形ADNM为矩形时,利用平行线的性质及待定系数法可求出直线AM的函数表达式,联立后可求出点M的坐标,再利用矩形的性质可求出点N的坐标.
【解答】解:(1)将B(2,0)代入y=﹣x2+c得:0=﹣4+c,
解得:c=4,
∴二次函数的表达式为y=﹣x2+4.
当y=0时,﹣x2+4=0,
解得:x1=﹣2,x2=2,
∴点A的坐标为(﹣2,0).
设直线AC的函数表达式为y=kx+b(k≠0),
将A(﹣2,0),C(0,2)代入y=kx+b得:,
解得:,
∴直线AC的函数表达式为y=x+2.
(2)联立直线AC和抛物线的函数表达式得:,
解得:,,
∴点D的坐标为(1,3),
∴S△ABD=×|2﹣(﹣2)|×|3|=6.
故答案为:6.
(3)当点Q在y轴正半轴轴时,过点Q作QE⊥AC于点E,如图1所示.
∵点A,B关于y轴对称,
∴AQ=BQ,
∵∠AQB=135°,
∴∠BAQ=(180°﹣135°)=22.5°.
∵点A的坐标为(﹣2,0),点C的坐标为(0,2),
∴OA=OC=2,
∴∠OAC=(180°﹣90°)=45°,AC=OA=2,
∴∠CAQ=∠OAC﹣∠BAQ=45°﹣22.5°=22.5°=∠BAQ,
∴AQ平分∠OAC,
∴OQ=EQ.
∵S△ACQ=CQ•OA=AC•EQ=AC•OQ,
∴(2﹣OQ)•2=2•OQ,
∴OQ=2﹣2,
∴点Q的坐标为(0,2﹣2).
当点Q在y轴负半轴时,点Q的坐标为(0,2﹣2).
故答案为:(0,2﹣2)或(0,2﹣2).
(4)连接BC,则AC⊥BC,即AD⊥BC,利用待定系数法可求出直线BC的函数表达式y=﹣x+2.
分两种情况考虑,如图2所示.
①当四边形ADMN为矩形时,设直线DM的函数表达式为y=﹣x+m,
将D(1,3)代入y=﹣x+m得:﹣1+m=3,
解得:m=4,
∴直线DM的函数表达式为y=﹣x+4.
联立直线DM和抛物线的函数表达式得:,
解得:,,
∴点M的坐标为(0,4),
又∵四边形ADMN为矩形,
∴点N的坐标为(﹣2+0﹣1,0+4﹣3),即(﹣3,1);
②当四边形ADNM为矩形时,同理可得出直线AM的函数表达式为y=﹣x﹣2,
联立直线AM和抛物线的函数表达式得:,
解得:,,
∴点M的坐标为(3,﹣5),
又∵四边形ADNM为矩形,
∴点N的坐标为(1+3﹣(﹣2),3﹣5﹣0),即(6,﹣2).
综上所述,存在这样的点N,使得以点A、点D、点M、点N为顶点的四边形是以AD为边的矩形,点N的坐标为(﹣3,1)或(6,﹣2).
6.(2022春•大同期末)如图,在平面直角坐标系中,直线l1:y=2x﹣1与x轴,y轴分别交于点A,B,直线l2:y=﹣x+1与x轴,y轴分别交于点P,C,连接AC,直线l1,l2交于点D.
(1)求点D的坐标,并直接写出不等式2x﹣1>﹣x+1的解集.
(2)求△ACD的面积.
(3)若点E在直线l1上,F为坐标平面内任意一点,试探究:是否存在以点B,C,E,F为顶点的四边形是矩形?若存在,请直接写出点F的坐标;若不存在,请说明理由.
【分析】(1)联立l1与l2的表达式可得点D的坐标,根据图象即可求解;
(2)由△ACD的面积=S△BCD﹣S△ABC,即可求解;
(3)设E(m,2m﹣1),分两种情况讨论,由矩形的性质可求解.
【解答】解:(1)联立l1与l2的表达式得:,解得:,
∴点D(,),
由图象得:不等式2x﹣1>﹣x+1的解集为x>;
(2)∵直线l1:y=2x﹣1与x轴,y轴分别交于点A,B,直线l2:y=﹣x+1与x轴,y轴分别交于点P,C,
∴点A(,0)、B(0,﹣1),C(0,1)、P(2,0),
则BC=2,
∵D(,),
∴△ACD的面积=S△BCD﹣S△ABC=×2×﹣×2×=;
(3)设E(m,2m﹣1),
∵B(0,﹣1),C(0,1),
∴BC2=4,
CE2=m2+(2m﹣1﹣1)2=5m2﹣8m+4,
BE2=m2+(2m﹣1+1)2=5m2,
如图,当BC为对角线时,
∵以点B,C,E,F为顶点的四边形是矩形,
∴∠BEC=90°,
∴BC2=CE2+BE2,
∴5m2﹣8m+4+5m2=4,
∴m=0(舍去)或,
∴E(,),
∴点F(﹣,﹣),
如图,当BC为边时,
∵以点E,C,B,F为顶点的四边形是矩形,
∴∠BCF=90°,
∴BE2=CE2+BC2,
∴5m2﹣8m+4+4=5m2,
∴m=1,
∴E(1,1),
∴点F(1,﹣2),
综上所述:点F坐标为(﹣,﹣)或(1,﹣2).
7.(2022春•平南县期末)如图,四边形OABC是矩形,点A、C分别在x轴、y轴上,△ODE是△OCB绕点O顺时针旋转90°得到的,点D在x轴上,直线BD交y轴于点F,交OE于点H,点B的坐标为(﹣2,4).
(1)求直线BD的表达式;
(2)求△DEH的面积;
(3)点M在x轴上,平面内是否存在点N,使以点D、F、M、N为顶点的四边形是矩形?若存在,请直接写出点N的坐标;若不存在,请说明理由.
【分析】(1)求出D点坐标,由待定系数法可求出答案;
(2)求出直线OE的解析式,联立直线OE和直线BD的解析式可求出H点的坐标,根据三角形面积公式可得出答案;
(3)分两种情况,由矩形的性质可求出答案.
【解答】解:(1)∵B(﹣2,4),
∴BC=2,OC=4,
∵△ODE是△OCB绕点O顺时针旋转90°得到的,
∴OD=OC=4,DE=BC=2,
∴D(4,0),
设直线BD解析式为y=kx+b,
把B、D坐标代入可得,
解得,
∴直线BD的解析式为y=﹣x+;
(2)由(1)可知E(4,2),设直线OE的解析式为y=mx,
∴4m=2,
∴m=,
∴直线OE的解析式为y=x,
联立,
解得,
∴H(,),
∴△DEH的面积==;
(3)当点M在x轴上时,
∵MF⊥BD,则直线MF的表达式为:y=x+,
当y=0,x=﹣,即点M(﹣,0),
点F向右平移4个单位向下平移单位得到D,
则点M向右平移4单位向下平移单位得到N,
则点N(,﹣);
当∠FMD=90°时,则可知M点为O点,如图,
∵四边形MFND为矩形,
∴NF=OD=4,ND=OF=,
∴N(4,);
综上可知存在满足条件的N点,其坐标为(,﹣)或(4,).
8.(2022春•东川区期末)如图,在四边形ABCD中,AB∥CD,∠ABC=90°,AD=CD=13cm,BC=12cm,M、N是线段AB、CD上两动点,M点从点A出发,以每秒2cm的速度沿AB方向运动,N点从点D出发,以每秒1cm的速度沿DC方向运动,M、N同时出发,同时停止,当M运动到点B时,M、N同时停止运动,设运动时间为t秒.
(1)求AB的长;
(2)当t为何值时,四边形AMCN为平行四边形?
(3)在M、N运动的过程中,是否存在四边形MBCN是矩形,若存在,请求出的t值;若不存在,请说明理由.
【分析】(1)过点C作AD的平行线CP交AB于点P,根据平行四边形的性质得到AP=DC=13cm,AD=PC=13cm,根据勾股定理得到,于是得到AB=AP+PB=13+5=18(cm);
(2)根据平行四边形的性质列方程即可得到结论;
(3)根据矩形的性质列方程得到18﹣2t=13﹣t,t=5(秒),根据矩形和平行四边形的判定即可得到结论.
【解答】解:(1)如图1,过点C作AD的平行线CP交AB于点P,
∵AB∥CD,
∴四边形APCD是平行四边形,
∴AP=DC=13cm,AD=PC=13cm,
在直角三角形PBC中,,
∴AB=AP+PB=13+5=18(cm);
(2)如图2,
∵AM∥NC,
∴当AM=NC时,四边形AMCN是平行四边形,
即:13﹣t=2t,
∴(秒),
当秒时,四边形AMCN是平行四边形;
(3)如图3,在M、N运动的过程中,存在四边形MBCN是矩形,理由如下:
当BM=CN时,四边形MBCN是矩形,
∴18﹣2t=13﹣t,t=5(秒),
当t=5秒时,BM=AB﹣AM=18﹣5×2=8(cm),
∴CN=DC﹣DN=13﹣5×1=8(cm),
∴BM=CN,
∵AB∥CD,
∴四边形MBCN是平行四边形,
∵∠ABC=90°
∴四边形MBCN是矩形.
9.(2022春•鄂城区期末)如图,在平面直角坐标系中,直线y=﹣x+6与x轴交于点A,与y轴交于点B,点C是线段OA上一点,把△COB沿直线BC翻折,点O恰好落在AB上的点D处,BC为折痕.
(1)求线段AB的长;
(2)求直线BC的解析式;
(3)若M是射线BC上的一个动点,在坐标平面内是否存在点P,使以A,B,M,P为顶点的四边形是以AB为一边的矩形?若存在,请求出点P的坐标;若不存在,请说明理由.
【分析】(1)求出A(8,0),B(0,6),即可求AB=10;
(2)由翻折可知:△OBC≌△DBC,则OC=CD,BD=OB=6,AD=AB﹣BD=4,设OC=x,则CD=x.AC=8﹣x,在Rt△ACD中,由勾股定理得x2+42=(8﹣x)2,解得:x=3,则C(3,0),即可求直线BC的解析式是y=﹣2x+6;
(3)当AB为矩形的边时,则有AB2+AM12=BM12,设M1(m,﹣2m+6),则AM12=5m2﹣40m+100,BM12=5m2,所以100+5m2﹣40m+100=5m2,解得m=5,则M1(5,﹣4),根据平移规律可得P1(﹣3,2).
【解答】解:(1)对于直线y=﹣x+6,
当x=0时,y=6,当y=0时,x=8,
∴A(8,0),B(0,6),
在直角△AOB中,AB==10;
(2)由翻折可知:△OBC≌△DBC,
∴OC=CD,BD=OB=6,AD=AB﹣BD=4,
设OC=x,则CD=x.AC=8﹣x,
在Rt△ACD中,由勾股定理得x2+42=(8﹣x)2,
解得:x=3,
即OC=3,则C(3,0),
设直线BC解析式为y=kx+b,
将点B(0,6),C(3,0)代入y=kx+b,
可得,
解得:k=2,b=6,
∴直线BC的解析式是y=﹣2x+6;
(3)①当AB为矩形的边时,如图所示,矩形AM1P1B,
则有AB2+AM12=BM12,
∵点M1在直线BC:y=﹣2x+6上,
设M1(m,﹣2m+6),则m>0,
∴AM12=(8﹣m)2+(﹣2m+6)2=5m2﹣40m+100,
BM12=m2+(6+2m﹣6)2=5m2,
∵AB2+AM12=BM12,
∴100+5m2﹣40m+100=5m2,
解得m=5,
∴M1(5,﹣4),
∵A(﹣8,0),B(0,6),
∴根据平移规律可得P1(﹣3,2);
满足条件的P点的坐标为(﹣3,2).
10.(2022春•叙州区期末)如图,四边形OABC是矩形,点A、C在坐标轴上,B点坐标(﹣1,2),△ODE是△OCB绕点O顺时针旋转90°得到,点D在x轴上,直线BD交y轴于点F.
(1)求直线BD的解析式;
(2)求△BCF的面积;
(3)点M在坐标轴上,平面内是否存在点N,使以点D、F、M、N为顶点的四边形是矩形?若存在,请直接写出点N的坐标;若不存在,请说明理由.
【分析】(1)根据旋转的性质得出D点的坐标,再用待定系数法求出直线BD的解析式即可;
(2)根据直线BD的解析式求出F点的坐标,根据B点和C点的坐标得出BC和CF的长度,即可计算面积;
(3)分∠MFD=90°,∠MDF=90°,∠FMD=90°三种情况分别讨论求出点N的坐标即可.
【解答】解:(1)∵△ODE是△OCB绕点O顺时针旋转90°得到的,
∴OD=OC=2,DE=BC=1,
∴D(2,0),
设直线BD的解析式为y=kx+b,
把B点和D点的坐标代入可得,
解得,
∴直线BD的解析式为y=﹣x+;
(2)由(1)知,直线BD的解析式为y=﹣x+,
∴F(0,),
∵B(﹣1,2),BC∥OA,
∴CF=2﹣=,
∴S△BCF=BC•CF=×1×=;
(3)存在,
∵以点D、F、M、N为顶点的四边形是矩形,
∴△DFM是直角三角形,
①当∠MFD=90°时,则M只能在x轴上,连接FN交MD于点G,如图,
由(2)可知,OF=,OD=2,
∵∠FMO+∠MFO=90°,∠FMO+∠FDO=90°,
∴∠MFO=∠FDO,
又∵∠MOF=∠FOD=90°,
∴△MOF∽△FOD,
∴,
即,
解得OM=,
∴M(﹣,0),且D(2,0),
∴G(,0),
设N点的坐标为(x,y),
则,,
解得x=,y=﹣,
此时N点的坐标为();
②当∠MDF=90°时,则M只能在y轴上,连接DN交MF于点G,如图,
同理①,△FOD∽△DOM,
∴,
即,
解得OM=3,
∴M(0,﹣3),且F(0,),
∴MG=MF=,
则OG=OM﹣MG=3﹣=,
∴G(0,﹣),
设N点的坐标为(x,y),
则,,
解得x=﹣2,y=﹣,
此时N(﹣2,﹣);
③当∠FMD=90°时,则可知M点为O点,如图,
∵四边形MFND为矩形,
∴NF=OD=2,ND=OF=,
∴此时N(2,);
综上可知,存在满足条件的N点,其坐标为(,﹣)或(﹣2,﹣)或(2,).
11.(2022春•梁子湖区期末)如图,在平面直角坐标系中,直线y=﹣x+6与x轴交于点A,与y轴交于点B.点C是线段OA上一点,把△COB沿直线BC翻折,点O恰好落在AB上的点D处,BC为折痕.
(1)求线段AB的长;
(2)求直线BC的解析式;
(3)若M是射线BC上的一个动点,在坐标平面内是否存在点P,使以A,B,M,P为顶点的四边形是以AB为一边的矩形?若存在,请求出点P的坐标;若不存在,请说明理由.
【分析】(1)分别求出A、B点坐标,即可求解;
(2)由折叠可知OC=CD,OB=CD,在Rt△ACD中,(8﹣OC)2=CO2+42,求出OC可知C点坐标,再由待定系数法求直线BC的解析式即可;
(3)设M(t,﹣2t+6),(t>0),P(x,y),当以AB为矩形的一边时,BM为矩形的对角线,则,过点M作EF∥x轴,过点A作AF⊥EF交于F,过点P作PE⊥EF交于点E,可得△AMF∽△MPE,则有=,求得t=5,再求P点坐标即可.
【解答】解:(1)令x=0,则y=6,
∴B(0,6),
令y=0,则x=8,
∴A(8,0),
∴AB=10;
(2)由折叠的性质可知,OC=CD,OB=CD,
∵OB=6,
∴BD=6,
∵AB=10,
∴AD=4,
在Rt△ACD中,AC2=CD2+AD2,
∴(8﹣OC)2=CO2+42,
∴CO=3,
∴C(3,0),
设直线BC的解析式为y=kx+b,
∴,
∴,
∴y=﹣2x+6;
(3)存在点P,使以A,B,M,P为顶点的四边形是以AB为一边的矩形,理由如下:
设M(t,﹣2t+6),(t>0),P(x,y),
当以AB为矩形的一边时,BM为矩形的对角线,
∴,
过点M作EF∥x轴,过点A作AF⊥EF交于F,过点P作PE⊥EF交于点E,
∵∠AMP=90°,
∴∠PME+∠AMF=90°,
∵∠AMF+∠MAF=90°,
∴∠AMF=∠PME,
∴△AMF∽△MPE,
∴=,
∵AF=2t﹣6,MF=8﹣t,PE=y+2t﹣6,EM=t﹣x,
∴=,
∴=,
解得t=5,
∴x=﹣3,y=2,
∴P(﹣3,2).
12.(2022•牡丹江)如图,在平面直角坐标系中,四边形ABCD,A在y轴的正半轴上,B,C在x轴上,AD∥BC,BD平分∠ABC,交AO于点E,交AC于点F,∠CAO=∠DBC.若OB,OC的长分别是一元二次方程x2﹣5x+6=0的两个根,且OB>OC.
请解答下列问题:
(1)求点B,C的坐标;
(2)若反比例函数y=(k≠0)图象的一支经过点D,求这个反比例函数的解析式;
(3)平面内是否存在点M,N(M在N的上方),使以B,D,M,N为顶点的四边形是边长比为2:3的矩形?若存在,请直接写出在第四象限内点N的坐标;若不存在,请说明理由.
【分析】(1)解方程的两个根就是OB,OC的长,再根据在x轴的正半轴上还是负半轴上就可以得到坐标;
(2)根据题意得∠BAC=∠BCA,所以AB=BC=5,又因为AD∥BC,所以∠ADB=∠DBC,即∠ABD=∠ADB,所以AB=AD=5,再根据勾股定理得AO的长,从而求解;
(3)先由勾股定理求出BD的长,再分两种情况:①当BD是矩形一边,又分BD是短边和长边时计算;②当BD是对角线时,以BD为半径作圆,可得符合题意的两个矩形进行计算,详情见解答过程.
【解答】解:(1)由x2﹣5x+6=0,解得x1=2,x2=3,
∵OB,OC的长分别是方程的两个根,且OB>OC,
∴OB=3,OC=2.
∴B(﹣3,0),C (2,0);
(2)∵AO⊥BC,
∴∠AOB=90°,
∵∠CAO=∠DBC,∠CAO+∠AFB=∠DBC+∠AOB,
∴∠AFB=∠AOB=90°.
∵BD平分∠ABC,
∴∠ABD=∠DBC,
∵∠AFB=90°,
∴∠BAC=∠BCA,
∴AB=BC=5,
∵AD∥BC,
∴∠ADB=∠DBC,
∴∠ABD=∠ADB,
∴AB=AD=5,
∵在Rt△ABO中,AO===4,
∴D(5,4),
∴反比例函数解析式为:y=;
(3)存在,N4(3,﹣12),N5(,﹣),N 6(,﹣),
理由:过点D作DG⊥x轴于点G,
∵B(﹣3,0),D(5,4),
∴BG=8,DG=4,BD==4,
∵使以B,D,M,N为顶点的四边形是边长比为2:3的矩形,
①当BD是矩形一边,且是短边时,即图中矩形BDM1N1和矩形BDM4N4,
由BD:N1B=2:3,得N1B=6,
过点N1作N1H⊥x轴于点H,由一线三等角易得△BDG∽△N1BH,
∴根据相似三角形三边对应成比例得:BH=6,N1H=12,
∴OH=OB+BH=3+6=9,
∴N1(﹣9,12),
同理得点N4(3,﹣12),
当BD是矩形一边,且是长边时,即图中矩形BDM2N2和矩形BDM3N3,
方法同上,得点N2(﹣,),N3(﹣,﹣);
②当BD是对角线时,如下图:以BD为半径作圆,矩形BN5DM5,BN6DM6即为符合题意矩形,
当BN5:N5D=2:3时,过点N5作KL∥x轴,过点B作BK⊥KL于点K,过点D作DL⊥KL于点L,
由一线三等角易得△BKN5∽△DLN5,
∴===,
∴BK=N5L,KN5=LD,
设N5L=x,LD=y,
∴BK=x,KN5=y,
∵N5L+KN5=8,DL﹣BK=4,
∴,
解得:,
∴KN5=y==,N5的横坐标=﹣3=,
同理得N5的纵坐标=﹣;
再同理得:当BN5:N5D=3:2时,N6(,﹣).
综上所述:在第四象限内点N的坐标为N4(3,﹣12),N5(,﹣),N 6(,﹣).
13.(2022春•岳麓区校级期末)如图,在平面直角坐标系中,直线y=mx+6交y轴于点C,交x轴于点D,且AD=OD,以OA和OC为邻边作矩形OABC,已知点B(﹣4,6),点E是直线AB上一动点.
(1)求m的值;
(2)如图1,若∠EDC=45°,求点E的坐标;
(3)若点M为射线DB上一点,点N为坐标平面内任意一点,是否存在以C,D,M,N为顶点的四边形是矩形,若存在,直接写出点N的坐标,若不存在,请说明理由.
【分析】(1)如图1,根据矩形的性质和AD=OD确定点D的坐标为(﹣2,0),代入直线y=mx+6中可得m的值;
(2)过E作EH⊥CD于H,过H作HK⊥x轴于K,过E作ET⊥HK于T,证明△ETH≌△HKD,得ET=HK,HT=DK,设ET=HK=a,HT=DK=b,可得E(﹣4,a+b),H(a﹣4,a),将H(a﹣4,a)代入y=3x+6得a=3,故E(﹣4,4);
(3)设M(t,﹣3t﹣6),N(c,d),又C(0,6),D(﹣2,0),分三种情况:根据矩形对角线互相平分且相等列方程,分别解方程组即可.
【解答】解:(1)∵四边形OABC是矩形,且B(﹣4,6),
∴OA=4,
∵AD=OD,
∴D(﹣2,0),
把D(﹣2,0)代入直线y=mx+6中得:
﹣2m+6=0,
解得:m=3;
答:m的值是3;
(2)过E作EH⊥CD于H,过H作HK⊥x轴于K,过E作ET⊥HK于T,如图:
由C(0,6),D(﹣2,0)得直线CD解析式为y=3x+6,
∵∠EDC=45°,
∴△EHD是等腰直角三角形,
∴EH=DH,∠DHK=90°﹣∠EHT=∠TEH,
∵∠ETH=90°=∠HKD,
∴△ETH≌△HKD(AAS),
∴ET=HK,HT=DK,
设ET=HK=a,HT=DK=b,
∴TK=HT+HK=b+a=AE,OK=OA﹣AK=4﹣a,
∴E(﹣4,a+b),H(a﹣4,a),
∵ET=AK,AD=OA﹣OD=4﹣2=2,
∴b=a﹣2,
∴E(﹣4,2a﹣2),
将H(a﹣4,a)代入y=3x+6得:
a=3(a﹣4)+6,
解得a=3,
∴E(﹣4,4);
(3)存在以C,D,M,N为顶点的四边形是矩形,理由如下:
由B(﹣4,6),D(﹣2,0)得直线BD解析式为y=﹣3x﹣6,
设M(t,﹣3t﹣6),N(c,d),又C(0,6),D(﹣2,0),
①若MN、CD为对角线,则MN、CD的中点重合,且MN=CD,
∴,
解得(舍去)或,
∴N(,);
②若MC、ND为对角线,则MC、ND的中点重合,且MC=ND,
∴,
解得(舍去),
∴这种情况不存在;
③若MD、NC若对角线,则MD、NC的中点重合,且MD=NC,
∴,
解得,
∴N(﹣,),
综上所述,N的坐标为:(,)或(﹣,).
14.(2022春•槐荫区期末)如图,平面直角坐标系中,O是坐标原点,直线y=kx+15(k≠0)经过点C(3,6),与x轴交于点A,与y轴交于点B.线段CD平行于x轴,交直线y=x于点D,连接OC,AD.
(1)填空:k= ﹣3 ,点A的坐标是 (5,0) ;
(2)求证:四边形OADC是平行四边形;
(3)动点P从点O出发,沿对角线OD以每秒1个单位长度的速度向点D运动,直到点D为止;动点Q同时从点D出发,沿对角线DO以每秒1个单位长度的速度向点O运动,直到点O为止.设两个点的运动时间均为t秒.
①当t=1时,△CPQ的面积是 12 ;
②是否存在t的值使得四边形CPAQ为矩形,若存在,请求出t的值;若不存在,请说明理由.
【分析】(1)代入C点坐标即可得出k值,确定直线的解析式,进而求出A点坐标即可;
(2)求出A、D点坐标,根据CD=OA,CD∥OA,即可证四边形OADC是平行四边形;
(3)①作CH⊥OD于H,设出H点的坐标,根据勾股定理计算出CH的长度,根据运动时间求出PQ的长度即可确定△CPQ的面积;
②先证四边形CPAQ为平行四边形,根据对角线相等确定PQ的长度,再根据P、Q的位置分情况计算出t值即可.
【解答】解:(1)∵直线y=kx+15(k≠0)经过点C(3,6),
∴3k+15=6,
解得:k=﹣3,
即直线的解析式为:y=﹣3x+15,
当y=0时,x=5,
∴A(5.0),
故答案为:﹣3,(5,0);
(2)∵线段CD平行于x轴,
∴D点的纵坐标与C点一样,
又∵D点在直线y=x上,
∴当y=6时,x=8,
即D(8,6),
∴CD=8﹣3=5,
∵OA=5,
∴OA=CD,
又∵OA∥CD,
∴四边形OADC是平行四边形;
(3)①作CH⊥OD于H,
,
∵H点在直线y=x上,
∴设H点的坐标为(m,m),
∴CH2=(m﹣3)2+(m﹣6)2,DH2=(m﹣8)2+(m﹣6)2,
由勾股定理,得CH2+DH2=CD2,
即(m﹣3)2+(m﹣6)2+(m﹣8)2+(m﹣6)2=52,
整理,得:m=或8(舍去),
∴CH=3,
∵OD==10,
∴当t=1时,PQ=OD﹣t﹣t=10﹣1﹣1=8,
∴S△CPQ=PQ•CH=×8×3=12,
故答案为:12;
②由(2)知四边形OADC是平行四边形,
∴OD与AC互相平分,
又∵P点和Q点的运动速度相同,
∴PQ与AC互相平分,
∴四边形CPAQ为平行四边形,
∵OD=10,
当0≤t≤5时,PQ=10﹣2t,
当5≤t≤10时,PQ=2t﹣10,
若当点P,Q运动至四边形CPAQ为矩形时,则PQ=AC,
∵AC==2,
当0≤t≤5时,10﹣2t=2,
解得t=5﹣,
当5≤t≤10时,2t﹣10=2,
解得t=5+,
综上,存在t的值使得四边形CPAQ为矩形,此时t的值为5﹣或5+.
15.(2022•武功县模拟)在平面直角坐标系中,已知抛物线L1:y=﹣x2+bx+c(b、c为常数)与x轴交于A(﹣6,0)、B(2,0)两点.
(1)求抛物线L1的函数表达式;
(2)将该抛物线L1向右平移4个单位长度得到新的抛物线L2,与原抛物线L1交于点C,点D是点C关于x轴的对称点,点N在平面直角坐标系中,请问在抛物线L2上是否存在点M,使得以点C、D、M、N为顶点的四边形是以CD为边的矩形?若存在,求出点M的坐标;若不存在,请说明理由.
【分析】(1)利用待定系数法直接求解即可;
(2)存在,根据题意求得抛物线L2的表达式,再与抛物线L1联立,求得点C的坐标,进而求得点D的坐标;要使得以点C、D、M、N为顶点的四边形是以CD为边的矩形,分当M在x轴上方时和当M在x轴下方时,两种情况讨论,根据矩形的性质列出方程,求解即可.
【解答】解:(1)把A(﹣6,0)、B(2,0)代入y=﹣x2+bx+c中,
得,
解得,
∴抛物线L1的函数表达式为y=﹣x2﹣4x+12;
(2)存在,理由如下:
∵y=﹣x2﹣4x+12=﹣(x+2)2+16,
∴抛物线L2的函数表达式为y=﹣(x+2﹣4)2+16=﹣(x﹣2)2+16=﹣x2+4x+12,
令﹣x2﹣4x+12=﹣x2+4x+12,
解得:x=0,
当x=0时,y=﹣x2﹣4x+12=12,
∴点C的坐标为(0,12),
∵点D是点C关于x轴的对称点,
∴点D坐标为(0,﹣12),
①当M在x轴上方时,
要使得以点C、D、M、N为顶点的四边形是以CD为边的矩形,
则yM=yC,即﹣x2+4x+12=12,
解得:x1=0,x2=4,
∴M1(4,12);
②当M在x轴下方时,
要使得以点C、D、M、N为顶点的四边形是以CD为边的矩形,
则yM=yD,即﹣x2+4x+12=﹣12,
解得:x1=2+2,x2=2﹣2,
M2(2+2,﹣12),M3(2﹣2,﹣12).
综上所述,在抛物线L2上是否存在点M,使得以点C、D、M、N为顶点的四边形是以CD为边的矩形,点M的坐标为(4,12)或(2+2,﹣12)或(2﹣2,﹣12).
16.(2022•阳明区校级模拟)如图,直线AB,CD分别与x轴交于B,C两点,与y轴交于A,D两点,且∠EAD=∠EDA,线段OB,OC的长分别是方程x2﹣8x+12=0的两根,并且OB=OA.
(1)求点D的坐标;
(2)求过点E的反比例函数解析式;
(3)若点M在坐标轴上,平面是否存在点N,使得以A,E,M,N为顶点的四边形为矩形?若存在,请写出满足条件的点N的个数,并任意写3个满足条件的点N的坐标;若不存在,说明理由.
【分析】(1)解方程求出OB,OC,再根据数量关系得出OA,利用三角函数求出OD,即可确定D点的坐标;
(2)用待定系数法求出直线CD和直线AB的解析式,联立两解析式求出E点坐标,即可得出过E点的反比例函数的解析式;
(3)根据M在坐标轴上,分情况讨论求出N的坐标即可.
【解答】解:(1)∵x2﹣8x+12=0,
解得x1=2,x2=6,
∴OB=2,OC=6,
∵OB=OA,∠EAD=∠EDA,
∴tan∠EAD=tan∠EDA==,
∴tan∠EDA=,
∴OD=12,
∴D(0,12);
(2)设直线CD的解析式为 y=kx+b ( k≠0 ),
分别把(﹣6,0),(0,﹣12)代入,
得
解得
∴直线CD的解析式为y=﹣2x﹣12,
同理直线AB的解析式y=2x+4,
联立
解得
∴E的坐标(﹣4,﹣4),
∴过点E的反比例函数解析式为;
(3)存在,根据题意要使得以A,E,M,N为顶点的四边形为矩形分以下几种情况:(写出其中三种即可)
①点M在x轴正半轴,且AE为边时,
∵∠BAO+∠OAM=90°,∠AMO+∠OAM=90°,
∴∠BAO=∠AMO,
∴tan∠AMO=tan∠BAO=,
即,
∵OA=2OB=4,
∴OM=2OA=8,
即M(8,0),
过N点作NH⊥x轴于H,
∵∠AMO+∠NMO=90°,∠NMO+∠HNM=90°,
∴∠AMO=∠HNM,
∴tan∠HNM=tan∠AMO=,
∵MN=AE==4,
设MH=a,则HN=2a,
∴a2+(2a)2=(4)2,
解得a=4或a=﹣4(舍去),
∴OH=8﹣a=4,HN=2a=8,
∴此时N(4,﹣8);
②当M点在x轴负半轴时,且AE为边时,
同理①可得M(﹣8,0),
作NP⊥x轴于点P,
同理①可得N(﹣4,8);
③M点在x轴,且AE为对角线时,
此时N点和M点都在x轴上,且BN=AB==2,
∴此时N点的坐标为(﹣2﹣2,0)或(2﹣2,0);
④M点在y轴上,且AE为对角线时,
此时M(0,﹣4),N(﹣4,4),
⑤M点在y轴上,且AE为边时,
∵tan∠BAO=,AE=4,
∴EM=2,
∴AM===10,
∴OM=AM﹣OA=10﹣4=6,
∴M(0,﹣6),
作NQ⊥OA于Q,
∵∠BAO+∠OAN=90°,∠ANQ+∠OAN=90°,
∴∠NAQ=∠BAO,
∴tan∠NAQ=tan∠BAO=,
设AQ=b,则NQ=2b,OQ=4﹣b,
∵AN=EM=2,
∴b2+(2b)2=(2)2,
解得b=2或﹣2(舍去),
∴OQ=4﹣2=2,NQ=4,
即此时N(4,2),
综上所述,符合条件的N点坐标为(﹣4,4),(4,2),(4,﹣8),(﹣4,8),(﹣2,0),(﹣2,0).
17.(2022•泸州)如图,在平面直角坐标系xOy中,已知抛物线y=ax2+x+c经过A(﹣2,0),B(0,4)两点,直线x=3与x轴交于点C.
(1)求a,c的值;
(2)经过点O的直线分别与线段AB,直线x=3交于点D,E,且△BDO与△OCE的面积相等,求直线DE的解析式;
(3)P是抛物线上位于第一象限的一个动点,在线段OC和直线x=3上是否分别存在点F,G,使B,F,G,P为顶点的四边形是以BF为一边的矩形?若存在,求出点F的坐标;若不存在,请说明理由.
【分析】(1)把A(﹣2,0),B(0,4)两点代入抛物线y=ax2+x+c中列方程组解出即可;
(2)利用待定系数可得直线AB的解析式,再设直线DE的解析式为:y=mx,点D是直线DE和AB的交点,列方程可得点D的横坐标,根据△BDO与△OCE的面积相等列等式可解答;
(3)设P(t,﹣t2+t+4),分两种情况:作辅助线构建相似三角形,证明三角形相似或利用等角的三角函数列等式可解答.
【解答】解:(1)把A(﹣2,0),B(0,4)两点代入抛物线y=ax2+x+c中得:
解得:;
(2)由(1)知:抛物线解析式为:y=﹣x2+x+4,
设直线AB的解析式为:y=kx+b,
则,解得:,
∴AB的解析式为:y=2x+4,
设直线DE的解析式为:y=mx,
∴2x+4=mx,
∴x=,
当x=3时,y=3m,
∴E(3,3m),
∵△BDO与△OCE的面积相等,CE⊥OC,
∴•3•(﹣3m)=•4•,
∴9m2﹣18m﹣16=0,
∴(3m+2)(3m﹣8)=0,
∴m1=﹣,m2=(舍),
∴直线DE的解析式为:y=﹣x;
(3)存在,
B,F,G,P为顶点的四边形是以BF为一边的矩形有两种情况:
设P(t,﹣t2+t+4),
①如图1,过点P作PH⊥y轴于H,
∵四边形BPGF是矩形,
∴BP=FG,∠PBF=∠BFG=90°,
∴∠CFG+∠BFO=∠BFO+∠OBF=∠CFG+∠CGF=∠OBF+∠PBH=90°,
∴∠PBH=∠OFB=∠CGF,
∵∠PHB=∠FCG=90°,
∴△PHB≌△FCG(AAS),
∴PH=CF,
∴CF=PH=t,OF=3﹣t,
∵∠PBH=∠OFB,
∴=,即=,
解得:t1=0(舍),t2=1,
∴F(2,0);
②如图2,过点G作GN⊥y轴于N,过点P作PM⊥x轴于M,
同①可得:NG=FM=3,OF=t﹣3,
∵∠OFB=∠FPM,
∴tan∠OFB=tan∠FPM,
∴=,即=,
解得:t1=,t2=(舍),
∴F(,0);
综上,点F的坐标为(2,0)或(,0).
18.(2022•平定县模拟)综合与探究
如图,抛物线与y轴交于点A(0,8),与x轴交于点B(6,0),C,过点A作AD∥x轴与抛物线交于另一点D.
(1)求抛物线的表达式;
(2)连接AB,点P为AB上一个动点,由点A以每秒1个单位长度的速度沿AB运动(不与点B重合),运动时间为t,过点P作PQ∥y轴交抛物线于点Q,求PQ与t的函数关系式;
(3)点M是y轴上的一个点,点N是平面直角坐标系内一点,是否存在这样的点M,N,使得以B,D,M,N为顶点的四边形是矩形?若存在,请直接写出点N的坐标;若不存在,请说明理由.
【分析】(1)将A(0,8),B(6,0)代入抛物线,解方程组即可得出结论;
(2)根据点A,B的坐标可得,直线AB的解析式为.过点P作PE⊥y轴于点E,可得△AEP∽△AOB,所以AE:EP:AP=AO:OB:AB=4:3:5.根据题意可知AP=t,所以,,所以点P的横坐标为.由此可得出PQ的长;
(3)要使以B,D,M,N为顶点的四边形是矩形,分以下情况进行讨论:过点B作x轴的垂线交AD的延长线于点E,则AE⊥EB;当DM为矩形的边时,过点N作NK⊥x轴,交x轴于点K;当DM'为矩形的对角线时,过点N'作N'K'⊥x轴交DA的延长线于点K';以BD为对角线,分别计算即可.
【解答】解:(1)将A(0,8),B(6,0)代入抛物线,
得,
解得.
∴抛物线的表达式为;
(2)设直线AB的解析式为y=kx+d,
将A,B两点坐标代入解析式得.
解得
∴直线AB的解析式为.
∵OA=8,OB=6,
∴由勾股定理可得.
如图,过点P作PE⊥y轴于点E,
∴∠AEP=∠AOB=90°,
∴EP∥OB.
则△AEP∽△AOB.
∴AE:EP:AP=AO:OB:AB=4:3:5.
根据题意可知AP=t,
∴,,
∴点P的横坐标为.
∴,
∴PQ与t的函数关系式为(0≤t<10);
(3)存在,点N的坐标为或.
要使以B,D,M,N为顶点的四边形是矩形,分以下情况进行讨论:
如图,过点B作x轴的垂线交AD的延长线于点E,则AE⊥EB,
当y=8时,,解得x=0或3.
∴点D的坐标为(3,8).
∴AD=3,DE=3.
①如图,当DM为矩形的边时,过点N作NK⊥x轴,交x轴于点K.
∵∠MAD=∠DEB=90°,∠ADM+∠BDE=90°,∠AMD+∠ADM=90°,
∴∠BDE=∠AMD.
∴△ADM∽△EBD.
∴,即,
∴.
同理,可求得△EBD∽△KBN.
∴△ADM∽△KBN,
∴∠MAD=∠NKB=90°,∠ADM=∠KBN,
又∵MD=NB,
∴△ADM≌△KBN.
∴AD=KB=3.
∴OK=6﹣3=3.
∴,
∴;
②如图,当DM'为矩形的对角线时,过点N'作N'K'⊥x轴交DA的延长线于点K'.
同理可得△M'BO∽△DBE,
∴,
∴,
∴.
∵DN'=BM',
∴△DN'K'≌△BM'O,
∴,K′D=OB=6,
∴AK'=3,点N'的纵坐=,
∴,
③以BD为对角线这种情况不存在.
综上所述,存在点M,N,使得以B,D,M,N为顶点的四边形是矩形,点N的坐标为或.
19.(2022•榆次区一模)综合与探究
如图,抛物线y=﹣x2+bx+c与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,点A,C的坐标分别为(﹣2,0),(0,4),连接AC,BC.点P是y轴右侧的抛物线上的一个动点.
(1)求抛物线的函数表达式,并直接写出点B的坐标;
(2)连接PA,交直线BC于点D,当线段AD的值最小时,求点P的坐标;
(3)点Q是坐标平面内一点,是否存在点Q,使得以点A,C,P,Q为顶点的四边形为矩形,若存在,请直接写出点Q的坐标;若不存在,请说明理由.
【分析】(1)将A(﹣2,0),C(0,4)代入y=﹣x2+bx+c,即可求解;
(2)当AD⊥BC时,AD的值最小,则∠DAB=45°,设P(t,﹣t2+t+4),过点P作PM⊥x轴交于点M,由PM=AM,可求P(2,4);
(3)设Q(x,y),P(m,﹣m2+m+4),分三种情况讨论:①当AQ为矩形对角线时,AQ=CP,可得,求得Q(7,);②当AP为矩形对角线时,AP=CQ,可得,求得Q(1,﹣);③当AC为矩形对角线时,AC=PQ,可得,此时Q点不存在.
【解答】解:(1)将A(﹣2,0),C(0,4)代入y=﹣x2+bx+c,
∴,
∴,
∴y=﹣x2+x+4,
令y=0,则﹣x2+x+4=0,
解得x=﹣2或x=4,
∴B(4,0);
(2)当AD⊥BC时,AD的值最小,
∵OB=OC=4,
∴∠CBO=45°,
∴∠DAB=45°,
设P(t,﹣t2+t+4),
过点P作PM⊥x轴交于点M,
∴PM=AM,
∴﹣t2+t+4=t+2,
解得t=2或t=﹣2,
∵点P是y轴右侧的抛物线上,
∴P(2,4);
(3)在点Q,使得以点A,C,P,Q为顶点的四边形为矩形,理由如下:
设Q(x,y),P(m,﹣m2+m+4),
①当AQ为矩形对角线时,AQ=CP,
∴,
解得或(舍),
∴Q(7,);
②当AP为矩形对角线时,AP=CQ,
∴,
解得或(舍),
∴Q(1,﹣);
③当AC为矩形对角线时,AC=PQ,
∴,
解得(舍)或(舍);
综上所述:Q点坐标为(7,)或(1,﹣).
20.(2022春•泰兴市校级月考)如图,在平面直角坐标系中,将抛物线C1:y=﹣(其中m为常数,且m<0)关于原点对称得到抛物线C2,抛物线C1,C2的顶点分别为M,N.
(1)请直接写出抛物线C2的表达式;(用含有m的式子表示)
(2)若抛物线C1与x轴的交点从左到右依次为A,B,抛物线C2与x轴的交点从左到右依次为C,D.
①若A,B,C,D四点从左到右依次排列,且AD=3BC,求m的值;
②是否存在这样的m,使以点M,A,N,D为顶点的四边形是矩形?若存在,求出m的值;若不存在,说明理由;
(3)在抛物线C1对称轴右侧的部分任取一点G,设直线MG,NG分别与y轴相交于P,Q两点,且GM=pGP,GN=qGQ,求p﹣q的值.
【分析】(1)设抛物线c2上任意一点(x,y),点(x,y)关于原点的对称点为(﹣x,﹣y),将点(﹣x,﹣y)代入抛物线,即可求解;
(2)①分别求出A(﹣1+m,0),B(1+m,0),C(﹣1﹣m,0),D(1﹣m,0),再由题意建立方程即可求m的值;
②由M、N关于原点对称,A、D关于原点对称,则MN为矩形的对角线,在由勾股定理可得1+3+(2m﹣1)2+3=12+4m2,解得m=﹣1;
(3)设G点的横坐标为t,过点G作x轴的平行线交y轴于点I,过点M作x轴的平行线交y轴于点H,过点N作y轴的平行线 交GI于点K,则GI∥MH,由平行线的性质可得=,即|t|=,再由NK∥y轴,得=,即|t|=,最后由等式=,可求p﹣q=2.
【解答】解:(1)设抛物线c2上任意一点(x,y),
则点(x,y)关于原点的对称点为(﹣x,﹣y),
将点(﹣x,﹣y)代入抛物线,
∴抛物线c2的解析式为y=(x+m)2﹣;
(2)①对函数,
令y=0,解得x=﹣1+m或x=1+m,
∵m<0,
∴A(﹣1+m,0),B(1+m,0),
对函数c2y=(x+m)2﹣,
令y=0,解得x=1﹣m或x=﹣1﹣m,
∵m<0,
∴C(﹣1﹣m,0),D(1﹣m,0),
∴AD=2﹣2m,BC=﹣2﹣2m,
∵AD=3BC,
∴2﹣2m=3(﹣2﹣2m),
∴m=﹣2;
②存在m,使以点M,A,N,D为顶点的四边形是矩形,理由如下:
∵抛物线c1的对称轴为x=m,
∴M(m,),
∵抛物线c2的对称轴为x=﹣m,
∴N(﹣m,﹣),
∵M、N关于原点对称,A、D关于原点对称,
∴MN为矩形的对角线,
∴AM2+AN2=MN2,
∴1+3+(2m﹣1)2+3=12+4m2,
解得m=﹣1;
(3)设G点的横坐标为t,
过点G作x轴的平行线交y轴于点I,过点M作x轴的平行线交y轴于点H,过点N作y轴的平行线交GI于点K,
∴GI∥MH,
∴=,
∵GM=pGP,
∴==,
∴|t|=,
∵NK∥y轴,
∴=,
∵GN=qGQ,
∴==,
∴|t|=,
∴=,
∴p﹣q=2.
21.(2022•黔东南州)如图,抛物线y=ax2+2x+c的对称轴是直线x=1,与x轴交于点A,B(3,0),与y轴交于点C,连接AC.
(1)求此抛物线的解析式;
(2)已知点D是第一象限内抛物线上的一个动点,过点D作DM⊥x轴,垂足为点M,DM交直线BC于点N,是否存在这样的点N,使得以A,C,N为顶点的三角形是等腰三角形.若存在,请求出点N的坐标,若不存在,请说明理由;
(3)已知点E是抛物线对称轴上的点,在坐标平面内是否存在点F,使以点B、C、E、F为顶点的四边形为矩形,若存在,请直接写出点F的坐标;若不存在,请说明理由.
【分析】(1)由抛物线的对称轴为直线x=1,抛物线经过点B(3,0),可得A(﹣1,0),用待定系数法即可求解;
(2)求出直线BC的解析式,设点D坐标为(t,﹣t2+2t+3),则点N(t,﹣t+3),利用勾股定理表示出AC2,AN2,CN2,然后分①当AC=AN时,②当AC=CN时,③当AN=CN时三种情况进行讨论,列出关于t的方程,求出t的值,即可写出点N的坐标;
(3)分两种情形讨论:①当BC为对角线时,②当BC为边时,先求出点E的坐标,再利用平行四边形的中心对称性求出点F的坐标即可.
【解答】解:(1)抛物线y=ax2+2x+c的对称轴是直线x=1,与x轴交于点A,B(3,0),
∴A(﹣1,0),
∴,解得,
∴抛物线的解析式y=﹣x2+2x+3;
(2)∵y=﹣x2+2x+3,
∴C(0,3),
设直线BC的解析式为y=kx+3,
将点B(3,0)代入得:0=3k+3,
解得:k=﹣1,
∴直线BC的解析式为y=﹣x+3;
设点D坐标为(t,﹣t2+2t+3),则点N(t,﹣t+3),
∵A(﹣1,0),C(0,3),
∴AC2=12+32=10,
AN2=(t+1)2+(﹣t+3)2=2t2﹣4t+10,
CN2=t2+(3+t﹣3)2=2t2,
①当AC=AN时,AC2=AN2,
∴10=2t2﹣4t+10,
解得t1=2,t2=0(不合题意,舍去),
∴点N的坐标为(2,1);
②当AC=CN时,AC2=CN2,
∴10=2t2,
解得t1=,t2=﹣(不合题意,舍去),
∴点N的坐标为(,3﹣);
③当AN=CN时,AN2=CN2,
∴2t2﹣4t+10=2t2,
解得t=,
∴点N的坐标为(,);
综上,存在,点N的坐标为(2,1)或(,3﹣)或(,);
(3)设E(1,a),F(m,n),
∵B(3,0),C(0,3),
∴BC=3,
①以BC为对角线时,BC2=CE2+BE2,
∴(3)2=12+(a﹣3)2+a2+(3﹣1)2,
解得:a=,或a=,
∴E(1,)或(1,),
∵B(3,0),C(0,3),
∴m+1=0+3,n+=0+3或n+=0+3,
∴m=2,n=或n=,
∴点F的坐标为(2,)或(2,);
②以BC为边时,BE2=CE2+BC2或CE2=BE2+BC2,
∴a2+(3﹣1)2=12+(a﹣3)2+(3)2或12+(a﹣3)2=a2+(3﹣1)2+(3)2,
解得:a=4或a=﹣2,
∴E(1,4)或(1,﹣2),
∵B(3,0),C(0,3),
∴m+0=1+3,n+3=0+4或m+3=1+0,n+0=3﹣2,
∴m=4,n=1或m=﹣2,n=1,
∴点F的坐标为(4,1)或(﹣2,1),
综上所述:存在,点F的坐标为(2,)或(2,)或(4,1)或(﹣2,1).
22.(2022•随州)如图1,平面直角坐标系xOy中,抛物线y=ax2+bx+c(a<0)与x轴分别交于点A和点B(1,0),与y轴交于点C,对称轴为直线x=﹣1,且OA=OC,P为抛物线上一动点.
(1)直接写出抛物线的解析式;
(2)如图2,连接AC,当点P在直线AC上方时,求四边形PABC面积的最大值,并求出此时P点的坐标;
(3)设M为抛物线对称轴上一动点,当P,M运动时,在坐标轴上是否存在点N,使四边形PMCN为矩形?若存在,直接写出点P及其对应点N的坐标;若不存在,请说明理由.
【分析】(1)判断出A,B两点坐标,可以假设抛物线的解析式为y=a(x+3)(x﹣1),把(0,3)代入抛物线的解析式,得a=﹣1,可得结论;
(2)如图(2)中,连接OP.设P(m,﹣m2﹣2m+3),构建二次函数,利用二次函数的性质求解即可;
(3)分两种情形,点N在y轴上,点N在x轴上,分别求解即可.
【解答】解:(1)∵抛物线的对称轴是直线x=﹣1,抛物线交x轴于点A,B(1,0),
∴A(﹣3,0),
∴OA=OC=3,
∴C(0,3),
∴可以假设抛物线的解析式为y=a(x+3)(x﹣1),
把(0,3)代入抛物线的解析式,得a=﹣1,
∴抛物线的解析式为y=﹣x2﹣2x+3;
(2)如图(2)中,连接OP.设P(m,﹣m2﹣2m+3),
S=S△PAO+S△POC+S△OBC,
=×3×(﹣m2﹣2m+3)××3×(﹣m)+×1×3
=(﹣m2﹣3m+4)
=﹣(m+)2+,
∵﹣<0,
∴当m=﹣时,S的值最大,最大值为,此时P(﹣,);
(3)存在,理由如下:
如图3﹣1中,当点N在y轴上时,四边形PMCN是矩形,此时P(﹣1,4),N(0,4);
如图3﹣2中,当四边形PMCN是矩形时,设M(﹣1,n),P(t,﹣t2﹣2t+3),则N(t+1,0),
由题意,,
解得,消去n得,3t2+5t﹣10=0,
解得t=,
∴P(,),N(,0)或P′(,),N′(,0).
综上所述,满足条件的点P(﹣1,4),N(0,4)或P(,),N(,0)或P′(,),N′(,0).
23.(2020•辽宁)如图,抛物线y=ax2﹣2x+c(a≠0)过点O(0,0)和A(6,0).点B是抛物线的顶点,点D是x轴下方抛物线上的一点,连接OB,OD.
(1)求抛物线的解析式;
(2)如图①,当∠BOD=30°时,求点D的坐标;
(3)如图②,在(2)的条件下,抛物线的对称轴交x轴于点C,交线段OD于点E,点F是线段OB上的动点(点F不与点O和点B重合),连接EF,将△BEF沿EF折叠,点B的对应点为点B',△EFB'与△OBE的重叠部分为△EFG,在坐标平面内是否存在一点H,使以点E,F,G,H为顶点的四边形是矩形?若存在,请直接写出点H的坐标,若不存在,请说明理由.
【分析】(1)利用待定系数法解决问题即可.
(2)如图①中,设抛物线的对称轴交x轴于M,与OD交于点N.解直角三角形求出点N的坐标,求出直线ON的解析式,构建方程组确定点D坐标即可.
(3)分三种情形:如图②﹣1中,当∠EFG=90°时,点H在第一象限,此时G,B′,O重合.如图②﹣2中,当∠EGF=90°时,点H在对称轴右侧.如图②﹣3中当∠FGE=90°时,点H在对称轴左侧,点B′在对称轴上,分别求解即可.
【解答】解:(1)把点O(0,0)和A(6,0)代入y=ax2﹣2x+c中,
得到,
解得,
∴抛物线的解析式为y=x2﹣2x.
(2)如图①中,设抛物线的对称轴交x轴于M,与OD交于点N.
∵y=x2﹣2x=(x﹣3)2﹣3,
∴顶点B(3,﹣3),M(3,0),
∴OM=3.BM=3,
∴tan∠MOB==,
∴∠MOB=60°,
∵∠BOD=30°,
∴∠MON=∠MOB﹣∠BOD=30°,
∴MN=OM•tan30°=,
∴N(3,﹣),
∴直线ON的解析式为y=﹣x,
由,解得或,
∴D(5,﹣).
(3)如图②﹣1中,当∠EFG=90°时,点H在第一象限,此时G,B′,O重合,由题意OF=BF,可得F(,﹣),E(3,﹣),利用平移的性质可得H(,).
如图②﹣2中,当∠EGF=90°时,点H在对称轴右侧,由题意,∠EBF=∠FEB=30°
∴EF=BF,可得F(2,﹣2),利用平移的性质可得H(,﹣).
如图②﹣3中当∠FGE=90°时,点H在对称轴左侧,点B′在对称轴上,由题意EF⊥BE,可得F(1,﹣),G(,﹣),利用平移的性质,可得H(,﹣).
综上所述,满足条件的点H的坐标为(,)或(,﹣)或(,﹣).
24.(2020•内乡县一模)如图,抛物线y=﹣x2+bx+c与x轴交于点A,B,与y轴交于点C,其中点B的坐标为(3,0),点C的坐标为(0,3),直线l经过B,C两点.
(1)求抛物线的解析式;
(2)过点C作CD∥x轴交抛物线于点D,过线段CD上方的抛物线上一动点E作EF⊥CD交线段BC于点F,求四边形ECFD的面积的最大值及此时点E的坐标;
(3)点P是在直线l上方的抛物线上一动点,点M是坐标平面内一动点,是否存在动点P,M,使得以C,B,P,M为顶点的四边形是矩形?若存在,请直接写出点P的横坐标;若不存在,请说明理由.
【分析】(1)将点B(3,0),点C(0,3)代入y=﹣x2+bx+c中,即可求解析式;
(2)求出BC的直线解析式为y=﹣x+3,设E(m,﹣m2+2m+3),则F(m,﹣m+3),所以S四ECFD=S△CDE+S△CDF=﹣m2+3m,即可求面积的最大值;
(3)设P(n,﹣n2+2n+3),①当CP⊥PB时,根据PJ=构建方程求解;②当CP⊥CB时,P(1,4),可求P点横坐标.
【解答】解:(1)将点B(3,0),点C(0,3)代入y=﹣x2+bx+c中,
则有,
∴,
∴y=﹣x2+2x+3;
(2)∵y=﹣x2+2x+3,
∴对称轴为x=1,
∵CD∥x轴,
∴D(2,3),
∴CD=2,
∵点B(3,0),点C(0,3),
∴BC的直线解析式为y=﹣x+3,
设E(m,﹣m2+2m+3),
∵EF⊥CD交线段BC于点F,
∴F(m,﹣m+3),
∴S四边形ECFD=S△CDE+S△CDF=×2×(﹣m2+2m)+×2×m=﹣m2+3m,
当m=时,四边形ECFD的面积最大,最大值为;
此时E(,);
(3)设P(n,﹣n2+2n+3),
①当CP⊥PB时,设BC的中点为J(,),
则有PJ=BC=,
∴(n﹣)2+(﹣n2+2n+3﹣)2=()2,
整理得n(n﹣3)(n2﹣n﹣1)=0,
∴n=0或3或,
∵P在第一象限,
∴P点横坐标为;
②当CP⊥CB时,P(1,4).
∴P点横坐标为1;
综上所述:P点横坐标为或1.
专题24函数与菱形存在性问题-中考数学压轴大题之经典模型培优案(全国通用): 这是一份专题24函数与菱形存在性问题-中考数学压轴大题之经典模型培优案(全国通用),文件包含专题24函数与菱形存在性问题-中考数学压轴大题之经典模型培优案解析版docx、专题24函数与菱形存在性问题-中考数学压轴大题之经典模型培优案原卷版docx等2份试卷配套教学资源,其中试卷共94页, 欢迎下载使用。
专题25函数与正方形存在性问题-中考数学压轴大题之经典模型培优案(全国通用): 这是一份专题25函数与正方形存在性问题-中考数学压轴大题之经典模型培优案(全国通用),文件包含专题25函数与正方形存在性问题-中考数学压轴大题之经典模型培优案解析版docx、专题25函数与正方形存在性问题-中考数学压轴大题之经典模型培优案原卷版docx等2份试卷配套教学资源,其中试卷共96页, 欢迎下载使用。
专题24函数与菱形存在性问题-中考数学压轴大题之经典模型培优案(全国通用): 这是一份专题24函数与菱形存在性问题-中考数学压轴大题之经典模型培优案(全国通用),文件包含专题24函数与菱形存在性问题-中考数学压轴大题之经典模型培优案解析版docx、专题24函数与菱形存在性问题-中考数学压轴大题之经典模型培优案原卷版docx等2份试卷配套教学资源,其中试卷共94页, 欢迎下载使用。












