

2023年广东省广州市中考数学模拟试卷(含答案)
展开2023年广东省广州中考数学模拟1
一.选择题(共10小题,满分30分,每小题3分)
1.(3分)(2020•广州)广州市作为国家公交都市建设示范城市,市内公共交通日均客运量已达15233000人次.将15233000用科学记数法表示应为( )
A.152.33×105 B.15.233×106
C.1.5233×107 D.0.15233×108
2.(3分)(2020•广州)某校饭堂随机抽取了100名学生,对他们最喜欢的套餐种类进行问卷调查后(每人选一种),绘制了如图的条形统计图,根据图中的信息,学生最喜欢的套餐种类是( )
A.套餐一 B.套餐二 C.套餐三 D.套餐四
3.(3分)(2020•广州)下列运算正确的是( )
A.+= B.2×3=6 C.x5•x6=x30 D.(x2)5=x10
4.(3分)(2020•广州)△ABC中,点D,E分别是△ABC的边AB,AC的中点,连接DE.若∠C=68°,则∠AED=( )
A.22° B.68° C.96° D.112°
5.(3分)(2021•广州)下列四个选项中,为负整数的是( )
A.0 B.﹣0.5 C.﹣ D.﹣2
6.(3分)(2021•广州)方程=的解为( )
A.x=﹣6 B.x=﹣2 C.x=2 D.x=6
7.(3分)(2021•广州)下列命题中,为真命题的是( )
(1)对角线互相平分的四边形是平行四边形
(2)对角线互相垂直的四边形是菱形
(3)对角线相等的平行四边形是菱形
(4)有一个角是直角的平行四边形是矩形
A.(1)(2) B.(1)(4) C.(2)(4) D.(3)(4)
8.(3分)(2021•广州)为了庆祝中国共产党成立100周年,某校举办了党史知识竞赛活动,在获得一等奖的学生中,有3名女学生,1名男学生,则从这4名学生中随机抽取2名学生,恰好抽到2名女学生的概率为( )
A. B. C. D.
9.(3分)(2022•广州)下列图形中,是中心对称图形的是( )
A. B.
C. D.
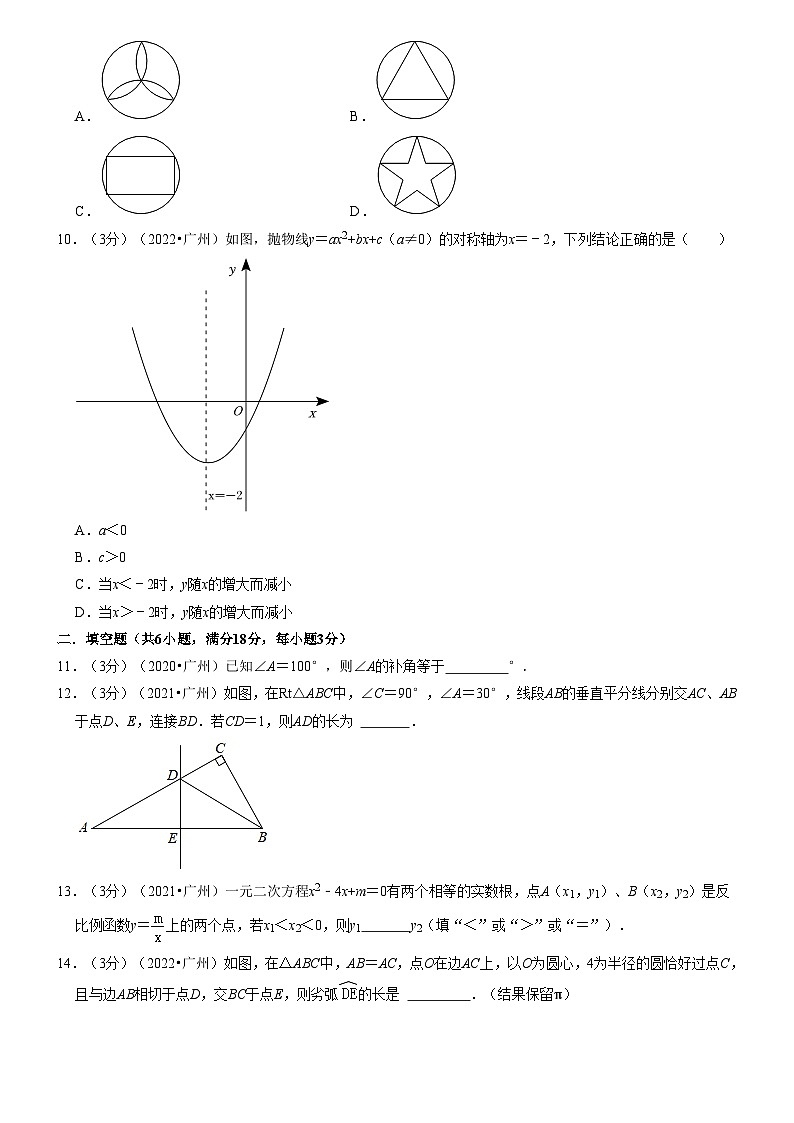
10.(3分)(2022•广州)如图,抛物线y=ax2+bx+c(a≠0)的对称轴为x=﹣2,下列结论正确的是( )
A.a<0
B.c>0
C.当x<﹣2时,y随x的增大而减小
D.当x>﹣2时,y随x的增大而减小
二.填空题(共6小题,满分18分,每小题3分)
11.(3分)(2020•广州)已知∠A=100°,则∠A的补角等于 °.
12.(3分)(2021•广州)如图,在Rt△ABC中,∠C=90°,∠A=30°,线段AB的垂直平分线分别交AC、AB于点D、E,连接BD.若CD=1,则AD的长为 .
13.(3分)(2021•广州)一元二次方程x2﹣4x+m=0有两个相等的实数根,点A(x1,y1)、B(x2,y2)是反比例函数y=上的两个点,若x1<x2<0,则y1 y2(填“<”或“>”或“=”).
14.(3分)(2022•广州)如图,在△ABC中,AB=AC,点O在边AC上,以O为圆心,4为半径的圆恰好过点C,且与边AB相切于点D,交BC于点E,则劣弧的长是 .(结果保留π)
15.(3分)(2022•广州)如图,在矩形ABCD中,BC=2AB,点P为边AD上的一个动点,线段BP绕点B顺时针旋转60°得到线段BP′,连接PP′,CP′.当点P′落在边BC上时,∠PP′C的度数为 ;当线段CP′的长度最小时,∠PP′C的度数为 .
16.(3分)(2020•广州)如图,正方形ABCD中,△ABC绕点A逆时针旋转到△AB'C',AB',AC'分别交对角线BD于点E,F,若AE=4,则EF•ED的值为 .
三.解答题(共9小题,满分102分)
17.(9分)(2020•广州)解不等式组:.
18.(9分)(2020•广州)如图,AB=AD,∠BAC=∠DAC=25°,∠D=80°.求∠BCA的度数.
19.(10分)(2022•广州)某数学活动小组利用太阳光线下物体的影子和标杆测量旗杆的高度.如图,在某一时刻,旗杆AB的影子为BC,与此同时在C处立一根标杆CD,标杆CD的影子为CE,CD=1.6m,BC=5CD.
(1)求BC的长;
(2)从条件①、条件②这两个条件中选择一个作为已知,求旗杆AB的高度.
条件①:CE=1.0m;条件②:从D处看旗杆顶部A的仰角α为54.46°.
注:如果选择条件①和条件②分别作答,按第一个解答计分.
参考数据:sin54.46°≈0.81,cos54.46°≈0.58,tan54.46°≈1.40.
20.(10分)(2022•广州)已知直线l:y=kx+b经过点(0,7)和点(1,6).
(1)求直线l的解析式;
(2)若点P(m,n)在直线l上,以P为顶点的抛物线G过点(0,﹣3),且开口向下.
①求m的取值范围;
②设抛物线G与直线l的另一个交点为Q,当点Q向左平移1个单位长度后得到的点Q′也在G上时,求G在≤x≤+1的图象的最高点的坐标.
21.(12分)(2021•广州)民生无小事,枝叶总关情,广东在“我为群众办实事”实践活动中推出“粤菜师傅”“广东技工”“南粤家政”三项培训工程,今年计划新增加培训共100万人次.
(1)若“广东技工”今年计划新增加培训31万人次,“粤菜师傅”今年计划新增加培训人次是“南粤家政”的2倍,求“南粤家政”今年计划新增加的培训人次;
(2)“粤菜师傅”工程开展以来,已累计带动33.6万人次创业就业,据报道,经过“粤菜师傅”项目培训的人员工资稳定提升,已知李某去年的年工资收入为9.6万元,预计李某今年的年工资收入不低于12.48万元,则李某的年工资收入增长率至少要达到多少?
22.(12分)(2020•广州)平面直角坐标系xOy中,抛物线G:y=ax2+bx+c(0<a<12)过点A(1,c﹣5a),B(x1,3),C(x2,3).顶点D不在第一象限,线段BC上有一点E,设△OBE的面积为S1,△OCE的面积为S2,S1=S2+.
(1)用含a的式子表示b;
(2)求点E的坐标:
(3)若直线DE与抛物线G的另一个交点F的横坐标为+3,求y=ax2+bx+c在1<x<6时的取值范围(用含a的式子表示).
23.(12分)(2021•广州)已知抛物线y=x2﹣(m+1)x+2m+3.
(1)当m=0时,请判断点(2,4)是否在该抛物线上;
(2)该抛物线的顶点随着m的变化而移动,当顶点移动到最高处时,求该抛物线的顶点坐标;
(3)已知点E(﹣1,﹣1)、F(3,7),若该抛物线与线段EF只有一个交点,求该抛物线顶点横坐标的取值范围.
24.(14分)(2020•广州)如图,⊙O为等边△ABC的外接圆,半径为2,点D在劣弧上运动(不与点A,B重合),连接DA,DB,DC.
(1)求证:DC是∠ADB的平分线;
(2)四边形ADBC的面积S是线段DC的长x的函数吗?如果是,求出函数解析式;如果不是,请说明理由;
(3)若点M,N分别在线段CA,CB上运动(不含端点),经过探究发现,点D运动到每一个确定的位置,△DMN的周长有最小值t,随着点D的运动,t的值会发生变化,求所有t值中的最大值.
25.(14分)(2021•广州)如图,在菱形ABCD中,∠DAB=60°,AB=2,点E为边AB上一个动点,延长BA到点F,使AF=AE,且CF、DE相交于点G.
(1)当点E运动到AB中点时,证明:四边形DFEC是平行四边形;
(2)当CG=2时,求AE的长;
(3)当点E从点A开始向右运动到点B时,求点G运动路径的长度.
2023年菁优广州中考数学终极押题密卷1
参考答案与试题解析
一.选择题(共10小题,满分30分,每小题3分)
1.(3分)(2020•广州)广州市作为国家公交都市建设示范城市,市内公共交通日均客运量已达15233000人次.将15233000用科学记数法表示应为( )
A.152.33×105 B.15.233×106
C.1.5233×107 D.0.15233×108
【考点】科学记数法—表示较大的数.版权所有
【专题】实数;运算能力.
【答案】C
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正整数;当原数的绝对值<1时,n是负整数.
【解答】解:15233000=1.5233×107,
故选:C.
【点评】此题考查了科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
2.(3分)(2020•广州)某校饭堂随机抽取了100名学生,对他们最喜欢的套餐种类进行问卷调查后(每人选一种),绘制了如图的条形统计图,根据图中的信息,学生最喜欢的套餐种类是( )
A.套餐一 B.套餐二 C.套餐三 D.套餐四
【考点】条形统计图.版权所有
【专题】统计的应用;数据分析观念.
【答案】A
【分析】根据条形统计图得出即可.
【解答】解:根据条形统计图可知:学生最喜欢的套餐种类是套餐一,
故选:A.
【点评】本题考查了条形统计图,能根据图形得出正确的信息是解此题的关键.
3.(3分)(2020•广州)下列运算正确的是( )
A.+= B.2×3=6 C.x5•x6=x30 D.(x2)5=x10
【考点】二次根式的混合运算;同底数幂的乘法;幂的乘方与积的乘方.版权所有
【专题】实数;运算能力.
【答案】D
【分析】各项计算得到结果,即可作出判断.
【解答】解:A、+=+,不符合题意;
B、原式=6a,不符合题意;
C、原式=x11,不符合题意;
D、原式=x10,符合题意.
故选:D.
【点评】此题考查了二次根式的混合运算,同底数幂的乘法,以及幂的乘方,熟练掌握运算法则是解本题的关键.
4.(3分)(2020•广州)△ABC中,点D,E分别是△ABC的边AB,AC的中点,连接DE.若∠C=68°,则∠AED=( )
A.22° B.68° C.96° D.112°
【考点】三角形中位线定理.版权所有
【专题】线段、角、相交线与平行线;三角形;推理能力.
【答案】B
【分析】根据三角形的中位线定理得到DE∥BC,根据平行线的性质即可求得∠AED=∠C=68°.
【解答】解:∵点D、E分别是△ABC的边AB、AC的中点,
∴DE∥BC,
∴∠AED=∠C,
∵∠C=68°,
∴∠AED=∠C=68°.
故选:B.
【点评】本题主要考查了三角形的中位线定理,能熟练地运用三角形的中位线定理是解此题的关键.
5.(3分)(2021•广州)下列四个选项中,为负整数的是( )
A.0 B.﹣0.5 C.﹣ D.﹣2
【考点】实数.版权所有
【专题】实数;数感.
【答案】D
【分析】根据整数的概念可以解答本题.
【解答】解:A、0是整数,但0既不是负数也不是正数,故此选项不符合题意;
B、﹣0.5是负分数,不是整数,故此选项不符合题意;
C、﹣是负无理数,不是整数,故此选项不符合题意;
D、﹣2是负整数,故此选项符合题意.
故选:D.
【点评】本题主要考查了实数的分类.明确大于0的整数是正整数,小于0的整数是负整数是解题的关键.
6.(3分)(2021•广州)方程=的解为( )
A.x=﹣6 B.x=﹣2 C.x=2 D.x=6
【考点】解分式方程.版权所有
【专题】计算题;分式方程及应用;运算能力.
【答案】D
【分析】求解分式方程,根据方程的解得结论.
【解答】解:去分母,得x=2x﹣6,
∴x=6.
经检验,x=6是原方程的解.
故选:D.
【点评】本题考查了解分式方程,掌握解分式方程的一般步骤是解决本题的关键.
7.(3分)(2021•广州)下列命题中,为真命题的是( )
(1)对角线互相平分的四边形是平行四边形
(2)对角线互相垂直的四边形是菱形
(3)对角线相等的平行四边形是菱形
(4)有一个角是直角的平行四边形是矩形
A.(1)(2) B.(1)(4) C.(2)(4) D.(3)(4)
【考点】命题与定理;平行四边形的判定;菱形的判定;矩形的判定.版权所有
【专题】多边形与平行四边形;矩形 菱形 正方形;推理能力.
【答案】B
【分析】利用平行四边形、矩形及菱形的判定方法分别判断后即可确定正确的选项.
【解答】解:(1)对角线互相平分的四边形是平行四边形,正确,为真命题,符合题意;
(2)对角线互相垂直的平行四边形是菱形,故原命题错误,是假命题,不符合题意;
(3)对角线相等的平行四边形是矩形,故原命题错误,为假命题,不符合题意;
(4)有一个角是直角的平行四边形是矩形,正确,是真命题,符合题意,
真命题为(1)(4),
故选:B.
【点评】考查了命题与定理的知识,解题的关键是了解平行四边形、矩形及菱形的判定方法,难度不大.
8.(3分)(2021•广州)为了庆祝中国共产党成立100周年,某校举办了党史知识竞赛活动,在获得一等奖的学生中,有3名女学生,1名男学生,则从这4名学生中随机抽取2名学生,恰好抽到2名女学生的概率为( )
A. B. C. D.
【考点】列表法与树状图法.版权所有
【专题】概率及其应用;数据分析观念;推理能力.
【答案】B
【分析】画树状图,共有12种等可能的结果,恰好抽到2名女学生的结果有6种,再由概率公式求解即可.
【解答】解:画树状图如图:
共有12种等可能的结果,恰好抽到2名女学生的结果有6种,
∴恰好抽到2名女学生的概率为=,
故选:B.
【点评】此题考查的是用列表法或树状图法求概率.列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件;树状图法适合两步或两步以上完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.
9.(3分)(2022•广州)下列图形中,是中心对称图形的是( )
A. B.
C. D.
【考点】中心对称图形.版权所有
【专题】平移、旋转与对称;几何直观.
【答案】C
【分析】根据中心对称图形的概念进行判断即可.
【解答】解:A.不是中心对称图形,故此选项不合题意;
B.不是中心对称图形,故此选项不合题意;
C.是中心对称图形,故此选项符合题意;
D.不是中心对称图形,故此选项不合题意;
故选:C.
【点评】本题考查的是中心对称图形的概念,中心对称图形是要寻找对称中心,旋转180度后与自身重合.
10.(3分)(2022•广州)如图,抛物线y=ax2+bx+c(a≠0)的对称轴为x=﹣2,下列结论正确的是( )
A.a<0
B.c>0
C.当x<﹣2时,y随x的增大而减小
D.当x>﹣2时,y随x的增大而减小
【考点】二次函数的性质.版权所有
【专题】二次函数图象及其性质;几何直观;推理能力.
【答案】C
【分析】根据图象得出a,c的符号即可判断A、B,利用二次函数的性质即可判断C、D.
【解答】解:∵图象开口向上,
∴a>0,故A不正确;
∵图象与y轴交于负半轴,
∴c<0,故B不正确;
∵抛物线开口向上,对称轴为直线x=﹣2,
∴当x<﹣2时,y随x的增大而减小,x>﹣2时,y随x的增大而增大,
故C正确,D不正确;
故选:C.
【点评】此题主要考查了二次函数图象和性质,熟练掌握二次函数的性质是解题关键.
二.填空题(共6小题,满分18分,每小题3分)
11.(3分)(2020•广州)已知∠A=100°,则∠A的补角等于 80 °.
【考点】余角和补角.版权所有
【专题】线段、角、相交线与平行线;运算能力.
【答案】80.
【分析】根据补角的概念求解可得.
【解答】解:∵∠A=100°,
∴∠A的补角=180°﹣100°=80°.
故答案为:80.
【点评】本题主要考查补角,解题的关键是掌握如果两个角的和等于180°(平角),就说这两个角互为补角.即其中一个角是另一个角的补角.
12.(3分)(2021•广州)如图,在Rt△ABC中,∠C=90°,∠A=30°,线段AB的垂直平分线分别交AC、AB于点D、E,连接BD.若CD=1,则AD的长为 2 .
【考点】含30度角的直角三角形;线段垂直平分线的性质.版权所有
【专题】线段、角、相交线与平行线;等腰三角形与直角三角形;推理能力.
【答案】2.
【分析】由线段垂直平分线的性质可得AD=BD,利用含30°角的直角三角形的性质可求解BD的长,进而求解.
【解答】解:∵DE垂直平分AB,
∴AD=BD,
∴∠A=∠ABD,
∵∠A=30°,
∴∠ABD=30°,
∴∠BDC=∠A+∠ABD=30°+30°=60°,
∵∠C=90°,
∴∠CBD=30°,
∵CD=1,
∴BD=2CD=2,
∴AD=2.
故答案为2.
【点评】本题主要考查线段的垂直平分线,含30° 角的直角三角形的性质,求得AD=BD是解题的关键.
13.(3分)(2021•广州)一元二次方程x2﹣4x+m=0有两个相等的实数根,点A(x1,y1)、B(x2,y2)是反比例函数y=上的两个点,若x1<x2<0,则y1 > y2(填“<”或“>”或“=”).
【考点】反比例函数图象上点的坐标特征;根的判别式.版权所有
【专题】一元二次方程及应用;反比例函数及其应用;运算能力.
【答案】>.
【分析】由一元二次方程根的情况,求得m的值,确定反比例函数y=图象经过的象限,然后根据反比例函数的性质即可求得结论.
【解答】解:∵一元二次方程x2﹣4x+m=0有两个相等的实数根,
∴Δ=16﹣4m=0,
解得m=4,
∵m>0,
∴反比例函数y=图象在一三象限,在每个象限y随x的增大而减少,
∵x1<x2<0,
∴y1>y2,
故答案为>.
【点评】本题考查了一元二次方程根的情况,反比例函数图象上点的坐标特征,熟练掌握反比例函数的性质是解题的关键.
14.(3分)(2022•广州)如图,在△ABC中,AB=AC,点O在边AC上,以O为圆心,4为半径的圆恰好过点C,且与边AB相切于点D,交BC于点E,则劣弧的长是 2π .(结果保留π)
【考点】弧长的计算;等腰三角形的性质;切线的性质.版权所有
【专题】几何图形;等腰三角形与直角三角形;运算能力;推理能力.
【答案】2π.
【分析】连接OD,OE,根据等腰三角形的性质和三角形内角和定理可得∠A=∠COE,再根据切线的性质和平角的定义可得∠DOE=90°,然后利用弧长公式进行计算即可解答.
【解答】解:如图,连接OD,OE,
∵OC=OE,
∴∠OCE=∠OEC,
∵AB=AC,
∴∠ABC=∠ACB,
∵∠A+∠ABC+∠ACB=∠COE+∠OCE+∠OEC,
∴∠A=∠COE,
∵OC=OE,
∴∠OCE=∠OEC,
∵圆O与边AB相切于点D,
∴∠ADO=90°,
∴∠COE+∠AOD=90°,
∴∠DOE=180°﹣(∠COE+∠AOD)=90°,
∴劣弧的长是=2π.
故答案为:2π.
【点评】本题考查了弧长的计算,等腰三角形的性质,熟练掌握切线的性质是解题的关键.
15.(3分)(2022•广州)如图,在矩形ABCD中,BC=2AB,点P为边AD上的一个动点,线段BP绕点B顺时针旋转60°得到线段BP′,连接PP′,CP′.当点P′落在边BC上时,∠PP′C的度数为 120° ;当线段CP′的长度最小时,∠PP′C的度数为 75° .
【考点】旋转的性质;矩形的性质.版权所有
【专题】平移、旋转与对称;推理能力.
【答案】120°,75°.
【分析】如图,以AB为边向右作等边△ABE,连接EP′.利用全等三角形的性质证明∠BEP′=90°,推出点P′在射线EP′上运动,如图1中,设EP′交BC于点O,再证明△BEO是等腰直角三角形,可得结论.
【解答】解:如图,以AB为边向右作等边△ABE,连接EP′.
∵△BPP′是等边三角形,
∴∠ABE=∠PBP′=60°,BP=BP′,BA=BE,
∴∠ABP=∠EBP′,
在△ABP和△EBP′中,
,
∴△ABP≌△EBP′(SAS),
∴∠BAP=∠BEP′=90°,
∴点P′在射线EP′上运动,
如图1中,设EP′交BC于点O,
当点P′落在BC上时,点P′与O重合,此时∠PP′C=180°﹣60°=120°,
当CP′⊥EP′时,CP′的长最小,此时∠EBO=∠OCP′=30°,
∴EO=OB,OP′=OC,
∴EP′=EO+OP′=OB+OC=BC,
∵BC=2AB,
∴EP′=AB=EB,
∴∠EBP′=∠EP′B=45°,
∴∠BP′C=45°+90°=135°,
∴∠PP′C=∠BP′C﹣∠BP′P=135°﹣60°=75°.
故答案为:120°,75°.
【点评】本题考查旋转的性质,矩形的性质,等边三角形的性质,全等三角形的判定和性质,等腰直角三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考填空题中的压轴题.
16.(3分)(2020•广州)如图,正方形ABCD中,△ABC绕点A逆时针旋转到△AB'C',AB',AC'分别交对角线BD于点E,F,若AE=4,则EF•ED的值为 16 .
【考点】旋转的性质;相似三角形的判定与性质;正方形的性质.版权所有
【专题】矩形 菱形 正方形;平移、旋转与对称;推理能力.
【答案】16.
【分析】根据正方形的性质得到∠BAC=∠ADB=45°,根据旋转的性质得到∠EAF=∠BAC=45°,根据相似三角形的性质即可得到结论.
【解答】解:∵四边形ABCD是正方形,
∴∠BAC=∠ADB=45°,
∵把△ABC绕点A逆时针旋转到△AB'C',
∴∠EAF=∠BAC=45°,
∵∠AEF=∠DEA,
∴△AEF∽△DEA,
∴=,
∴EF•ED=AE2,
∵AE=4,
∴EF•ED的值为16,
故答案为:16.
【点评】本题考查了旋转的性质,正方形的性质,相似三角形的判定和性质,找出相关的相似三角形是解题的关键.
三.解答题(共9小题,满分102分)
17.(9分)(2020•广州)解不等式组:.
【考点】解一元一次不等式组.版权所有
【专题】一元一次不等式(组)及应用;运算能力.
【答案】x≥3.
【分析】根据不等式的性质求出两个不等式的解集,进而求出不等式组的解集即可.
【解答】解:
解不等式①得:x≥3,
解不等式②得:x>2,
所以不等式组的解集为:x≥3.
【点评】本题考查了一元一次不等式组的解法:解一元一次不等式组时,一般先求出其中各不等式的解集,再求出这些解集的公共部分,解集的规律:同大取大;同小取小;大小小大中间找;大大小小找不到.
18.(9分)(2020•广州)如图,AB=AD,∠BAC=∠DAC=25°,∠D=80°.求∠BCA的度数.
【考点】全等三角形的判定与性质.版权所有
【专题】图形的全等;几何直观.
【答案】75°.
【分析】运用SAS公理,证明△ABC≌△ADC,得到∠D=∠B=80°,再根据三角形内角和为180°即可解决问题.
【解答】解:在△ABC与△ADC中,
,
∴△ABC≌△ADC(SAS),
∴∠D=∠B=80°,
∴∠BCA=180°﹣25°﹣80°=75°.
【点评】主要考查了全等三角形的判定及其性质的应用问题;应牢固掌握全等三角形的判定及其性质,这是灵活运用的基础和关键.
19.(10分)(2022•广州)某数学活动小组利用太阳光线下物体的影子和标杆测量旗杆的高度.如图,在某一时刻,旗杆AB的影子为BC,与此同时在C处立一根标杆CD,标杆CD的影子为CE,CD=1.6m,BC=5CD.
(1)求BC的长;
(2)从条件①、条件②这两个条件中选择一个作为已知,求旗杆AB的高度.
条件①:CE=1.0m;条件②:从D处看旗杆顶部A的仰角α为54.46°.
注:如果选择条件①和条件②分别作答,按第一个解答计分.
参考数据:sin54.46°≈0.81,cos54.46°≈0.58,tan54.46°≈1.40.
【考点】解直角三角形的应用﹣仰角俯角问题.版权所有
【专题】解直角三角形及其应用;运算能力.
【答案】(1)BC的长为8m;
(2)旗杆AB的高度约为12.8m.
【分析】(1)根据已知BC=5CD,进行计算即可解答;
(2)若选择条件①,根据同一时刻的物高与影长是成比例的,进行计算即可解答;
若选择条件②,过点D作DF⊥AB,垂足为F,根据题意可得DC=BF=1.6m,DF=BC=8m,然后在Rt△ADF中,利用锐角三角函数的定义求出AF的长,进行计算即可解答.
【解答】解:(1)∵BC=5CD,CD=1.6m,
∴BC=5×1.6=8(m),
∴BC的长为8m;
(2)若选择条件①:
由题意得:
=,
∴=,
∴AB=12.8,
∴旗杆AB的高度为12.8m;
若选择条件②:
过点D作DF⊥AB,垂足为F,
则DC=BF=1.6m,DF=BC=8m,
在Rt△ADF中,∠ADF=54.46°,
∴AF=DF•tan54.46°≈8×1.4=11.2(m),
∴AB=AF+BF=11.2+1.6=12.8(m),
∴旗杆AB的高度约为12.8m.
【点评】本题考查了解直角三角形的应用﹣仰角俯角问题,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
20.(10分)(2022•广州)已知直线l:y=kx+b经过点(0,7)和点(1,6).
(1)求直线l的解析式;
(2)若点P(m,n)在直线l上,以P为顶点的抛物线G过点(0,﹣3),且开口向下.
①求m的取值范围;
②设抛物线G与直线l的另一个交点为Q,当点Q向左平移1个单位长度后得到的点Q′也在G上时,求G在≤x≤+1的图象的最高点的坐标.
【考点】二次函数综合题.版权所有
【专题】二次函数图象及其性质;运算能力;应用意识.
【答案】(1)y=﹣x+7;
(2)①m<10且m≠0;
②(﹣2,9)或(2,5).
【分析】(1)用待定系数法求解析式即可;
(2)①设抛物线的解析式为y=a(x﹣m)2+7﹣m,将点(0,﹣3)代入可得am2+7﹣m=﹣3,再由a=<0,求m的取值即可;
②由题意求出Q点的横坐标为m+,联立方程组,整理得ax2+(1﹣2ma)x+am2﹣m=0,根据根与系数的关系可得m+m+=2m﹣,可求a=﹣2,从而可求m=2或m=﹣,确定抛物线的解析式后即可求解.
【解答】解:(1)将点(0,7)和点(1,6)代入y=kx+b,
∴,
解得,
∴y=﹣x+7;
(2)①∵点P(m,n)在直线l上,
∴n=﹣m+7,
设抛物线的解析式为y=a(x﹣m)2+7﹣m,
∵抛物线经过点(0,﹣3),
∴am2+7﹣m=﹣3,
∴a=,
∵抛物线开口向下,
∴a<0,
∴a=<0,
∴m<10且m≠0;
②∵抛物线的对称轴为直线x=m,
∴Q点与Q'关于x=m对称,
∴Q点的横坐标为m+,
联立方程组,
整理得ax2+(1﹣2ma)x+am2﹣m=0,
∵P点和Q点是直线l与抛物线G的交点,
∴m+m+=2m﹣,
∴a=﹣2,
∴y=﹣2(x﹣m)2+7﹣m,
∴﹣2m2+7﹣m=﹣3,
解得m=2或m=﹣,
当m=2时,y=﹣2(x﹣2)2+5,
此时抛物线的对称轴为直线x=2,
图象在≤x≤上的最高点坐标为(2,5);
当m=﹣时,y=﹣2(x+)2+,
此时抛物线的对称轴为直线x=﹣,
图象在﹣2≤x≤﹣1上的最高点坐标为(﹣2,9);
综上所述:G在≤x≤+1的图象的最高点的坐标为(﹣2,9)或(2,5).
【点评】本题考查二次函数的图象及性质,熟练掌握二次函数的图象及性质,会用待定系数法求函数的解析式,分类讨论是解题的关键.
21.(12分)(2021•广州)民生无小事,枝叶总关情,广东在“我为群众办实事”实践活动中推出“粤菜师傅”“广东技工”“南粤家政”三项培训工程,今年计划新增加培训共100万人次.
(1)若“广东技工”今年计划新增加培训31万人次,“粤菜师傅”今年计划新增加培训人次是“南粤家政”的2倍,求“南粤家政”今年计划新增加的培训人次;
(2)“粤菜师傅”工程开展以来,已累计带动33.6万人次创业就业,据报道,经过“粤菜师傅”项目培训的人员工资稳定提升,已知李某去年的年工资收入为9.6万元,预计李某今年的年工资收入不低于12.48万元,则李某的年工资收入增长率至少要达到多少?
【考点】一元一次不等式的应用;一元一次方程的应用.版权所有
【专题】一次方程(组)及应用;一元一次不等式(组)及应用;应用意识.
【答案】见试题解答内容
【分析】(1)设“南粤家政”今年计划新增加培训x万人次,则“粤菜师傅”今年计划新增加培训2x万人次,根据今年计划新增加培训共100万人次,即可得出关于x的一元一次方程,解之即可得出结论;
(2)设李某的年工资收入增长率为m,利用李某今年的年工资收入=李某去年的年工资收入×(1+增长率),结合预计李某今年的年工资收入不低于12.48万元,即可得出关于m的一元一次不等式,解之即可得出m的取值范围,再取其中的最小值即可得出结论.
【解答】解:(1)设“南粤家政”今年计划新增加培训x万人次,则“粤菜师傅”今年计划新增加培训2x万人次,
依题意得:31+2x+x=100,
解得:x=23.
答:“南粤家政”今年计划新增加培训23万人次.
(2)设李某的年工资收入增长率为m,
依题意得:9.6(1+m)≥12.48,
解得:m≥0.3=30%.
答:李某的年工资收入增长率至少要达到30%.
【点评】本题考查了一元一次方程的应用以及一元一次不等式的应用,解题的关键是:(1)找准等量关系,正确列出一元一次方程;(2)根据各数量之间的关系,正确列出一元一次不等式.
22.(12分)(2020•广州)平面直角坐标系xOy中,抛物线G:y=ax2+bx+c(0<a<12)过点A(1,c﹣5a),B(x1,3),C(x2,3).顶点D不在第一象限,线段BC上有一点E,设△OBE的面积为S1,△OCE的面积为S2,S1=S2+.
(1)用含a的式子表示b;
(2)求点E的坐标:
(3)若直线DE与抛物线G的另一个交点F的横坐标为+3,求y=ax2+bx+c在1<x<6时的取值范围(用含a的式子表示).
【考点】二次函数综合题.版权所有
【专题】二次函数图象及其性质;应用意识.
【答案】见试题解答内容
【分析】(1)将点A坐标代入解析式可求解;
(2)分两种情况讨论,由三角形面积关系,可得BE=CE+1,由对称轴为x=3,可求BC中点M的坐标(3,3),由线段的数量关系,可求EM=,可求解;
(3)先求出点F坐标,点D坐标可求直线DF解析式,可得点E坐标,可求DE解析式,可得c=9a,由二次函数的性质可求解.
【解答】解:(1)∵抛物线G:y=ax2+bx+c(0<a<12)过点A(1,c﹣5a),
∴c﹣5a=a+b+c,
∴b=﹣6a;
(2)如图1,当点B在点C的左边时,设BC的中点为M,
∵B(x1,3),C(x2,3),线段BC上有一点E,
∴S1=×BE×3=BE,S2=×CE×3=CE,
∵S1=S2+.
∴CE+=BE,
∴BE=CE+1,
∵b=﹣6a,
∴抛物线G:y=ax2﹣6ax+c,
∴对称轴为x==3,
∴BC的中点M坐标为(3,3),
∵BE=BM+EM,CE=CM﹣EM,BM=CM,BE=CE+1,
∴EM=,
∴点E(,3)
当点B在点C的右边时,设BC的中点为M,
同理可求点E(,3),
综上所述:点E(,3)或(,3);
(3)∵直线DE与抛物线G:y=ax2﹣6ax+c的另一个交点F的横坐标为+3,
∴y=a()2﹣6a×(+3)+c=﹣9a+c,
∴点F(+3,﹣9a+c),
∵点D是抛物线的顶点,
∴点D(3,﹣9a+c),
∴直线DF的解析式为:y=6x﹣18+c﹣9a,
∵点E坐标为(,3),
又∵点D(3,﹣9a+c),
∴直线DE解析式为:y=(6+18a﹣2c)x+7c﹣63a﹣18,
∵直线DE与直线DF是同一直线,
∴6=6+18a﹣2c,
∴c=9a,
∴抛物线解析式为:y=ax2﹣6ax+9a,
∵1<x<6,
∴当x=3时,ymin=0,当x=6时,ymax=9a,
∴0≤y<9a.
【点评】本题是二次函数综合题,考查了二次函数的性质,待定系数法求解析式,三角形面积公式,一次函数图象的性质,求出c=9a是本题的关键.
23.(12分)(2021•广州)已知抛物线y=x2﹣(m+1)x+2m+3.
(1)当m=0时,请判断点(2,4)是否在该抛物线上;
(2)该抛物线的顶点随着m的变化而移动,当顶点移动到最高处时,求该抛物线的顶点坐标;
(3)已知点E(﹣1,﹣1)、F(3,7),若该抛物线与线段EF只有一个交点,求该抛物线顶点横坐标的取值范围.
【考点】二次函数综合题.版权所有
【专题】综合题;函数思想;待定系数法;函数的综合应用;运算能力;应用意识.
【答案】(1)点(2,4)不在抛物线上;
(2)(2,5);
(3)x顶点<﹣或x顶点>或x顶点=1.
【分析】(1)当m=0时,抛物线为y=x2﹣x+3,将x=2代入得y=5,故点(2,4)不在抛物线上;
(2)抛物线y=x2﹣(m+1)x+2m+3的顶点为(,),而=﹣(m﹣3)2+5,即得m=3时,纵坐标最大,此时顶点移动到了最高处,顶点坐标为:(2,5);
(3)求出直线EF的解析式为y=2x+1,由得直线y=2x+1与抛物线y=x2﹣(m+1)x+2m+3的交点为:(2,5)和(m+1,2m+3),因(2,5)在线段EF上,由已知可得(m+1,2m+3)不在线段EF上,即是m+1<﹣1或m+1>3,或(2,5)与(m+1,2m+3)重合,可得抛物线顶点横坐标x顶点=<﹣或x顶点=>或x顶点=1.
【解答】解:(1)当m=0时,抛物线为y=x2﹣x+3,
将x=2代入得y=4﹣2+3=5,
∴点(2,4)不在抛物线上;
(2)抛物线y=x2﹣(m+1)x+2m+3的顶点为(,),
化简得(,),
顶点移动到最高处,即是顶点纵坐标最大,
而=﹣(m﹣3)2+5,
∴m=3时,纵坐标最大,即是顶点移动到了最高处,
此时该抛物线解析式为y=x2﹣4x+9,顶点坐标为:(2,5);
(3)设直线EF解析式为y=kx+b,将E(﹣1,﹣1)、F(3,7)代入得:
,解得,
∴直线EF的解析式为y=2x+1,
由得:或,
∴直线y=2x+1与抛物线y=x2﹣(m+1)x+2m+3的交点为:(2,5)和(m+1,2m+3),
而(2,5)在线段EF上,
∴若该抛物线与线段EF只有一个交点,则(m+1,2m+3)不在线段EF上,或(2,5)与(m+1,2m+3)重合,
∴m+1<﹣1或m+1>3或m+1=2(此时2m+3=5),
∴此时抛物线顶点横坐标x顶点=<﹣或x顶点=>或x顶点===1.
【点评】本题考查二次函数的综合应用,涉及图象上点坐标特征,顶点坐标,抛物线与线段交点等知识,解题的关键是用m的代数式表示抛物线与直线交点的坐标.
24.(14分)(2020•广州)如图,⊙O为等边△ABC的外接圆,半径为2,点D在劣弧上运动(不与点A,B重合),连接DA,DB,DC.
(1)求证:DC是∠ADB的平分线;
(2)四边形ADBC的面积S是线段DC的长x的函数吗?如果是,求出函数解析式;如果不是,请说明理由;
(3)若点M,N分别在线段CA,CB上运动(不含端点),经过探究发现,点D运动到每一个确定的位置,△DMN的周长有最小值t,随着点D的运动,t的值会发生变化,求所有t值中的最大值.
【考点】圆的综合题.版权所有
【专题】等腰三角形与直角三角形;平移、旋转与对称;圆的有关概念及性质;推理能力.
【答案】见试题解答内容
【分析】(1)由等边三角形的性质可得∠ABC=∠BAC=∠ACB=60°,圆周角定理可得∠ADC=∠BDC=60°,可得结论;
(2)将△ADC绕点C逆时针旋转60°,得到△BHC,可证△DCH是等边三角形,可得四边形ADBC的面积S=S△ADC+S△BDC=S△CDH=CD2,即可求解;
(3)作点D关于直线AC的对称点E,作点D关于直线BC的对称点F,由轴对称的性质可得EM=DM,DN=NF,可得△DMN的周长=DM+DN+MN=FN+EM+MN,则当点E,点M,点N,点F四点共线时,△DMN的周长有最小值,即最小值为EF=t,由轴对称的性质可求CD=CE=CF,∠ECF=120°,由等腰三角形的性质和直角三角形的性质可求EF=2PE=EC=CD=t,则当CD为直径时,t有最大值为4.
【解答】证明:(1)∵△ABC是等边三角形,
∴∠ABC=∠BAC=∠ACB=60°,
∵∠ADC=∠ABC=60°,∠BDC=∠BAC=60°,
∴∠ADC=∠BDC,
∴DC是∠ADB的平分线;
(2)四边形ADBC的面积S是线段DC的长x的函数,
理由如下:
如图1,将△ADC绕点C逆时针旋转60°,得到△BHC,
∴CD=CH,∠DAC=∠HBC,
∵四边形ACBD是圆内接四边形,
∴∠DAC+∠DBC=180°,
∴∠DBC+∠HBC=180°,
∴点D,点B,点H三点共线,
∵DC=CH,∠CDH=60°,
∴△DCH是等边三角形,
∵四边形ADBC的面积S=S△ADC+S△BDC=S△CDH=CD2,
∴S=x2(2<x≤4);
(3)如图2,作点D关于直线AC的对称点E,作点D关于直线BC的对称点F,
∵点D,点E关于直线AC对称,
∴EM=DM,
同理DN=NF,
∵△DMN的周长=DM+DN+MN=FN+EM+MN,
∴当点E,点M,点N,点F四点共线时,△DMN的周长有最小值,
则连接EF,交AC于M,交BC于N,连接CE,CF,DE,DF,作CP⊥EF于P,
∴△DMN的周长最小值为EF=t,
∵点D,点E关于直线AC对称,
∴CE=CD,∠ACE=∠ACD,
∵点D,点F关于直线BC对称,
∴CF=CD,∠DCB=∠FCB,
∴CD=CE=CF,∠ECF=∠ACE+∠ACD+∠DCB+∠FCB=2∠ACB=120°,
∵CP⊥EF,CE=CF,∠ECF=120°,
∴EP=PF,∠CEP=30°,
∴PC=EC,PE=PC=EC,
∴EF=2PE=EC=CD=t,
∴当CD有最大值时,EF有最大值,即t有最大值,
∵CD为⊙O的弦,
∴CD为直径时,CD有最大值4,
∴t的最大值为4.
【点评】本题是圆的综合题,考查了圆的有关知识,等边三角形的性质,旋转的性质,轴对称的性质等知识,灵活运用这些性质进行推理是本题的关键.
25.(14分)(2021•广州)如图,在菱形ABCD中,∠DAB=60°,AB=2,点E为边AB上一个动点,延长BA到点F,使AF=AE,且CF、DE相交于点G.
(1)当点E运动到AB中点时,证明:四边形DFEC是平行四边形;
(2)当CG=2时,求AE的长;
(3)当点E从点A开始向右运动到点B时,求点G运动路径的长度.
【考点】四边形综合题.版权所有
【专题】综合题;几何直观.
【答案】见试题解答内容
【分析】(1)利用平行四边形的判定定理:两边平行且相等的四边形是平行四边形,
(2)利用三角形相似,求出此时FG的长,再借助直角三角形勾股定理求解,
(3)利用图形法,判断G点轨迹为一条线段,在对应点处求解.
【解答】解:(1)证明:连接DF,CE,如图所示:
,
∵E为AB中点,
∴AE=AF=AB,
∴EF=AB=CD,
∵四边形ABCD是菱形,
∴EF∥CD,
∴四边形DFEC是平行四边形.
(2)作CH⊥BH,设AE=FA=m,如图所示,
,
∵四边形ABCD是菱形,
∴CD∥EF,
∴△CDG∽△FEG,
∴,
∴FG=2m,
在Rt△CBH中,∠CBH=60°,BC=2,
sin60°=,CH=,
cos60°=,BH=1,
在Rt△CFH中,CF=2+2m,CH=,FH=3+m,
CF2=CH2+FH2,
即(2+2m)2=()2+(3+m)2,
整理得:3m2+2m﹣8=0,
解得:m1=,m2=﹣2(舍去),
∴.
(3)G点轨迹为线段AG,
证明:如图,
(此图仅作为证明AG轨迹用),
延长线段AG交CD于H,作HM⊥AB于M,作DN⊥AB于N,
∵四边形ABCD是菱形,
∴BF∥CD,
∴△DHG∽△EGA,△HGC∽△AGF,
∴,,
∴,
∵AE=AF,
∴DH=CH=1,
在Rt△ADN中,AD=2,∠DAB=60°.
∴sin60°=,DN=.cos60°=,AN=1,
在Rt△AHM中,HM=DN=,AM=AN+NM=AN+DH=2,
tan∠HAM=,
G点轨迹为线段AG.
∴G点轨迹是线段AG.
如图所示,作GH⊥AB,
∵四边形ABCD为菱形,∠DAB=60°,AB=2,
∴CD∥BF,BD=2,
∴△CDG∽△FBG,
∴,即BG=2DG,
∵BG+DG=BD=2,
∴BG=,
在Rt△GHB中,BG=,∠DBA=60°,
sin60°=,GH=,
cos60°=,BH=,
在Rt△AHG中,AH=2﹣=,GH=,
AG2=()2+()2=,
∴AG=.
∴G点路径长度为.
解法二:如图,连接AG,延长AG交CD于点W.
∵CD∥BF,
∴=,=,
∴=,
∵AF=AE,
∴DW=CW,
∴点G在AW上运动.
下面的解法同上.
【点评】本题主要考查平行四边形的判定,菱形的性质,解题关键是借助锐角三角比和勾股定理求解.
2023学年广东省广州市中考数学模拟考试卷(含答案): 这是一份2023学年广东省广州市中考数学模拟考试卷(含答案),共12页。
2023年广东省广州市中考数学模拟试卷(六)(含答案): 这是一份2023年广东省广州市中考数学模拟试卷(六)(含答案),共13页。
2023年广东省广州市中考数学模拟3(含答案): 这是一份2023年广东省广州市中考数学模拟3(含答案),共22页。












