北师大版八年级下册2 直角三角形授课课件ppt

这是一份北师大版八年级下册2 直角三角形授课课件ppt，共21页。PPT课件主要包含了导入新课，观察与思考，讲授新课，等边对等角，等角对等边，归纳总结，∵DEBC，典例精析，∵ADAE，合作探究等内容，欢迎下载使用。
1.能用所学的知识证明等边三角形的判定定理.(重点)2.掌握含30°角的直角三角形的性质并解决有关问题.(难点)
观察下面图片，说说它们都是由什么图形组成的？
思考：上节课我们学习了等腰三角形的判定定理，那等边三角形的判定定理是什么呢？
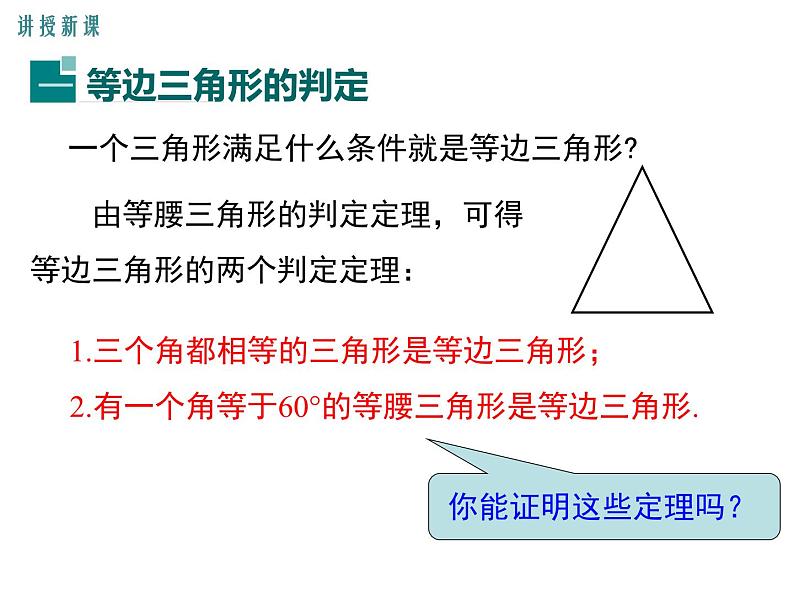
一个三角形满足什么条件就是等边三角形?
由等腰三角形的判定定理，可得等边三角形的两个判定定理：
1.三个角都相等的三角形是等边三角形；2.有一个角等于60°的等腰三角形是等边三角形.
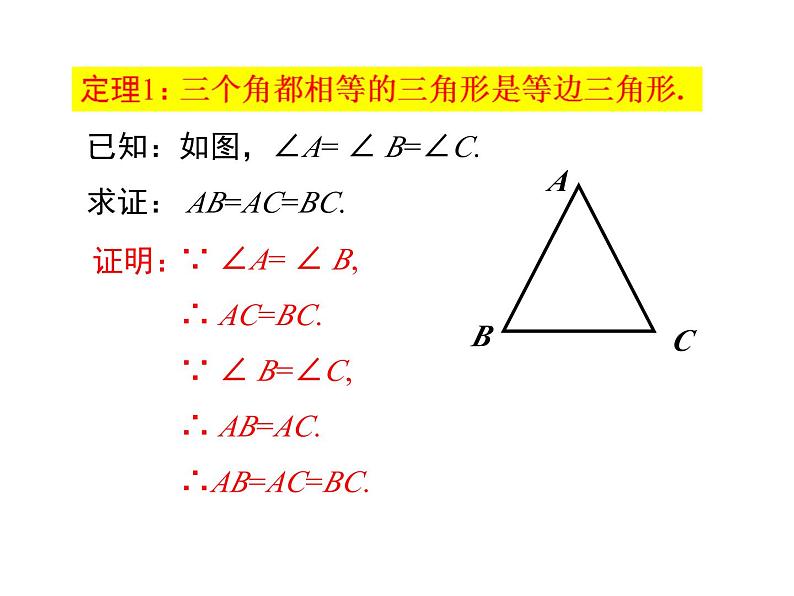
已知：如图，∠A= ∠ B=∠C.求证： AB=AC=BC.
∵ ∠A= ∠ B,∴ AC=BC.∵ ∠ B=∠C,∴ AB=AC.∴AB=AC=BC.
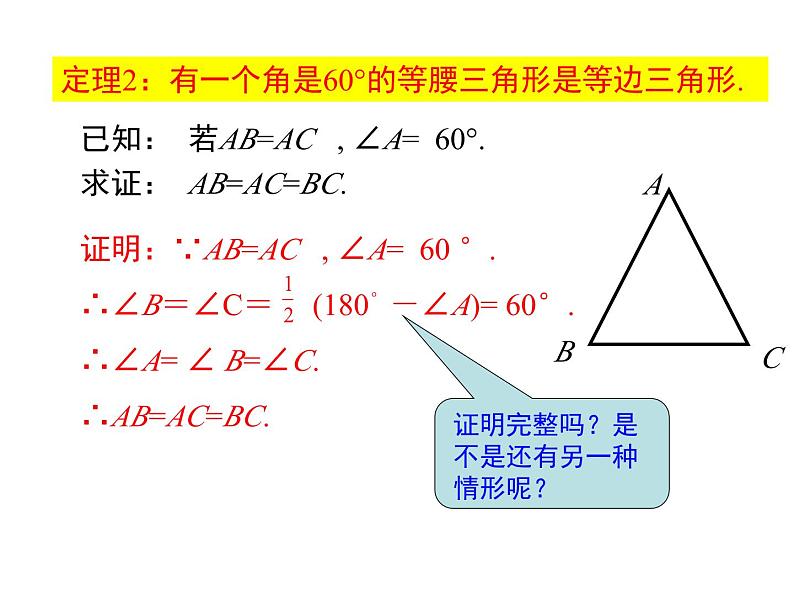
定理2：有一个角是60°的等腰三角形是等边三角形.
已知： 若AB=AC , ∠A= 60°.求证： AB=AC=BC.
证明：∵AB=AC , ∠A= 60 °.∴∠B＝∠C＝ (180。－∠A)= 60°.∴∠A= ∠ B=∠C.∴AB=AC=BC.
证明:∵AB=AC,∠B=60°(已知),∴∠C=∠B=60°(等边对等角)，∴∠A=60°(三角形内角和定理)．∴∠A=∠B =∠C=60°． ∴△ABC是等边三角形(三个角都相等的三角形是等边三角形).
已知:如图,在△ABC中，AB=AC,∠B=60°．求证:△ABC是等边三角形．
第二种情况：有一个底角是60°.
“三线合一”,即等腰三角形顶角平分线，底边上的中线、高线互相重合
有一角是60°的等腰三角形是等边三角形
等边三角形三个内角都相等，且每个角都是60°
三个角都相等的三角形是等边三角形
例1 如图,在等边三角形ABC中，DE∥BC, 求证：△ADE是等边三角形.
∵ △ABC是等边三角形，
∴ ∠A= ∠B= ∠C.
∴ ∠ADE= ∠B, ∠ AED= ∠C.
∴ ∠A= ∠ADE= ∠ AED.
∴ △ADE是等边三角形.
想一想：本题还有其他证法吗？
变式：上题中,若将条件DE∥BC改为AD=AE, △ADE还是等边三角形吗?试说明理由.
如图,在等边三角形ABC中，AD=AE, 求证：△ADE是等边三角形.
∴ ∠A= ∠B= ∠C=60°.
∴ △ADE是等腰三角形
∴ △ADE是等边三角形.
又∵ ∠A=60°.
操作:用两个含有30°角的三角板，你能拼成一个怎样的三角形？
你能说出所拼成的三角形的形状吗？
猜想：在直角三角形中, 30°角所对的直角边与斜边有怎样的大小关系？
已知:如图,在△ABC中,∠ACB=90°，∠A=30°.求证:BC= AB.
分析：突破如何证明“线段的倍、分”问题
∵ ∠ACB=90°, (已知) ∴∠ACD=90°，(平角意义)在△ABC与△ADC中， BC=DC，（作图）　∠ACB=∠ACD，（已证） AC=AC，（公共边） ∴△ABC≌△ADC（SAS） ， ∴ AD=AB； ∵∠ACB=90°,∠BAC=30°，(已知) ∴∠B=60°， ∴△ABD是等边三角形，(有一个角是60°的等腰三角形是等边三角形) ∴BC= BD= AB． (等式性质)
证明: 延长BC至D,使CD=BC,连接AD，
定理:在直角三角形中, 如果有一个锐角等于30°,那么它所对的直角边等于斜边的一半．
几何语言：在△ABC中,∵∠ACB=90°,∠A=30°．∴BC= AB．(在直角三角形中, 30°角所对的直角边等于斜边的一半)
例2 如图，在△ABC中，已知AB=AC=2a,∠B=∠ACB=15°, CD是腰AB上的高，求CD的长.
解：∵∠B=∠ACB=15°，(已知) ∴∠DAC=∠B+∠ACB= 15°+15°=30°， ∵∠ADC=90°，∴CD= AC=a．（在直角三角形中, 如果有一个锐角等于30°,那么它所对的直角边等于斜边的一半）
例3 已知:如图,在△ABC中，∠ACB=90°，∠A=30°，CD⊥AB于D．求证:BD=
证明：∵∠A=30°，CD⊥AB，∠ACB=90°∴BC= ∠B=60°．∴∠BCD=30°， ∴BD=∴BD=
1.已知△ABC中，∠A=∠B=60°，AB=3cm，则△ABC的周长为______cm.
2.在△ABC中，∠B＝90°，∠C＝30°，AB＝3．则AC=_____;BC=_______．
3. 已知：如图，AB=BC ，∠CDE= 120°， DF∥BA，且DF平分∠CDE.求证：△ABC是等边三角形.
∴△ABC是等边三角形.
又∵∠CDE=120°，DF平分∠CDE.
∴ ∠FDC=∠ABC=60°，
∴ △ABC是等腰三角形，
∴ ∠EDF=∠FDC=60°，
证明：延长BC至D，使CD=BC，连接AD.∵∠ACB=90°，∴∠ACD=90°．又∵AC=AC．∴△ACB≌△ACD(SAS)．∴AB=AD．∵CD=BC，∴BC=　BD．又∵BC= 　AB，∴AB=BD．∴AB=AD=BD，即△ABD是等边三角形．∴∠B=60°．在Rt△ABC中，∠BAC=30°．
4．已知：在Rt△ABC中，∠C=90°, BC= AB．求证：∠BAC=30°．