陕西省商洛市2021-2022学年高一数学下学期期末试题（Word版附解析）

商洛市2021～2022学年度第二学期期末教学质量检测

高一数学试卷

考生注意：

1．本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共150分.考试时间120分钟.

2．请将各题答案填写在答题卡上.

3．本试卷主要考试内容：北师大版必修3，必修4.

第Ⅰ卷

一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．

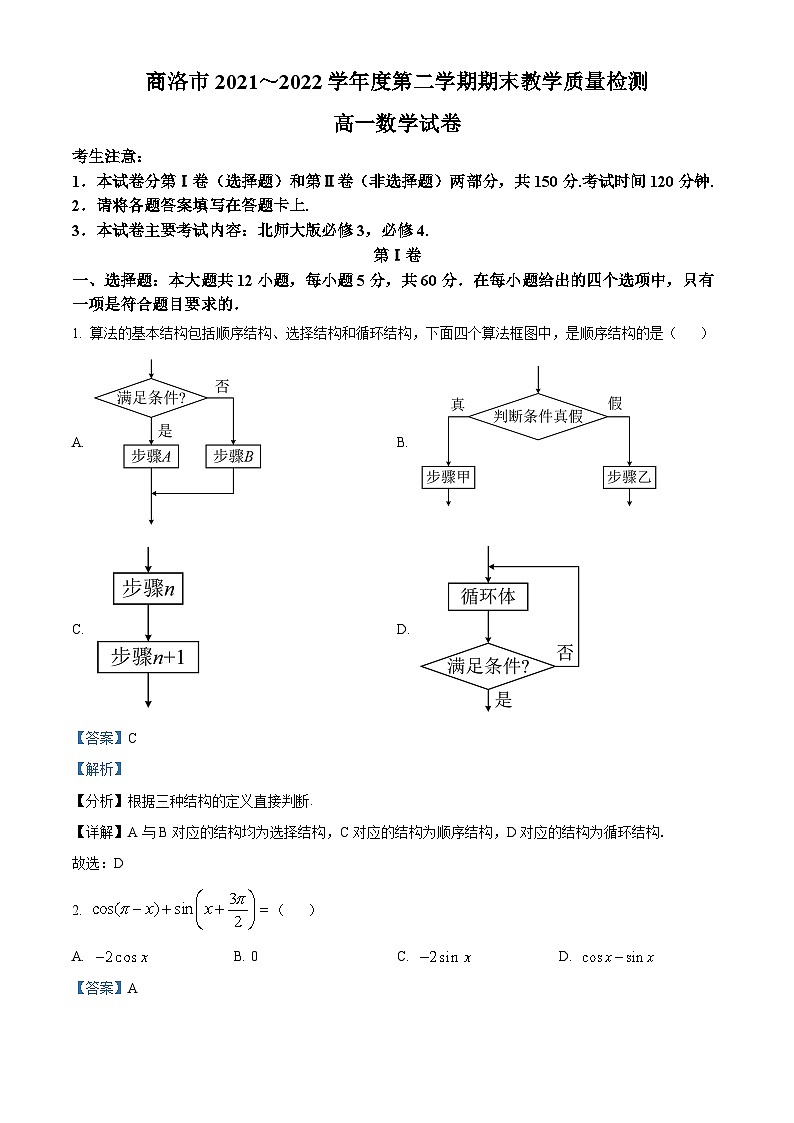
1. 算法的基本结构包括顺序结构、选择结构和循环结构，下面四个算法框图中，是顺序结构的是（    ）

A.  B.

C.  D.

【答案】C

【解析】

【分析】根据三种结构的定义直接判断.

【详解】A与B对应的结构均为选择结构，C对应的结构为顺序结构，D对应的结构为循环结构.

故选：D

2. （    ）

A.  B. 0 C.  D.

【答案】A

【解析】

【分析】由诱导公式直接化简可得.

【详解】

故选：A

3. （    ）

A  B.  C.  D.

【答案】D

【解析】

【分析】根据平面向量的线性运算求解即可

【详解】

故选：D

4. 函数的最小正周期与最小值分别为（    ）

A.  B.  C.  D.

【答案】C

【解析】

【分析】根据正弦函数的周期，最值求解．

【详解】

故选：C．

5. 从甲、乙等五人中任选两人参加某公司的剪彩仪式，则甲、乙恰有一人未入选的概率为（    ）

A. 0.3 B. 0.4 C. 0.6 D. 0.7

【答案】C

【解析】

【分析】利用列举法得到所有的基本事件个数，然后根据古典概型直接计算即可.

【详解】记五人分别为1，2，3，甲，乙. 任选两人共有（1，2），（1，3），(1,甲)，（1，乙），（2，3），（2，甲），（2，乙），（3，甲），（3，乙），（甲，乙）共10个样本点，其中

甲、乙恰有一人未入选的情况有(1,甲)，（1，乙），（2，甲），（2，乙），（3，甲），（3，乙）共6个样本点，则所求概率为．

答案选：C.

6. 一个扇形的半径为3，圆心角为，且周长为8，则（    ）

A.  B.  C.  D.

【答案】B

【解析】

【分析】根据扇形的中心角公式计算．

【详解】设扇形的弧长为l，则，则

故选：B．

7. 某工厂一天生产某种机器零件2000个（编号依次为0001，0002，…，2000），要求产品检验员当天抽取50件零件，检查其质量状况．若采用系统抽样，且编号为0005的零件被抽取，则编号在区间内的零件被抽取的件数为（    ）

A. 4 B. 5 C. 6 D. 7

【答案】C

【解析】

【分析】根据系统抽样的概念求解．

【详解】依题意可得抽样距为，因为编号为0005的零件被抽取，所以其他被抽取的零件的编号依次为0045，0085，0125，0165，0205，0245，0285，0325，0365，0405，0445，…，故编号在区间内的零件被抽取的件数为6．

故选：C．

8. 已知函数，要得到函数的图象，只需将函数的图象（    ）

A. 向左平移个单位长度 B. 向左平移个单位长度

C. 向右平移个单位长度 D. 向右平移个单位长度

【答案】B

【解析】

【分析】利用三角函数诱导公式将函数化为，根据三角函数图象的平移变换，可得答案.

【详解】由于，

故只需将函数的图象向左平移个单位长度，即得到，

也即图象，

故选：B

9. 我国明朝数学家程大位著的《算法统宗》里有一道闻名世界的题目：“一百馒头一百僧，大僧三个更无争，小僧三人分一个，大小和尚各几丁？”如图所示的程序框图反映了对此题的一个求解算法，则输出的（    ）

A. 25 B. 45 C. 55 D. 75

【答案】A

【解析】

【分析】根据程序框图依次计算可得.

【详解】；；；；；．

所以

故选：A

10. 已知，且，则（    ）

A.  B.  C.  D.

【答案】C

【解析】

【分析】使用诱导公式及两角和与差得余弦解决.

【详解】因为，所以．

又，

所以，

故

故选：C.

11. 已知向量满足，则的最大值为（    ）

A.  B.  C.  D.

【答案】A

【解析】

【分析】化简可得，进而根据数量积的性质得，从而得到的最大值

【详解】，因为，，所以，，所以.又，，所以，当且仅当与反向时，等号成立，所以的最大值为36+6.

故选：A

12. 已知函数，若与在区间内的零点个数之和为4，则的取值范围是（    ）

A.  B.  C.  D.

【答案】A

【解析】

【分析】先根据零点存在定理判断零点的个数，得到零点个数，列不等式求解.

【详解】因为为增函数，且，根据零点存在定理，所以在内存在唯一的零点，根据的单调性可知其在内存在唯一的零点，又与在区间内的零点个数之和为4，所以在区间内的零点个数为．由，得，则，此时恰好包含：三个零点，解得．

故选：A

第Ⅱ卷

二、填空题：本大题共4小题，每小题5分，共20分．把答案填在答题卡中的横线上．

13. 已知向量，且，则___________．

【答案】

【解析】

【分析】由向量平行的坐标表示计算．

【详解】因为，所以，解得．

故答案：．

14. 据文献记载，《百家姓》成文于北宋初年，表1记录了《百家姓》开头的24大姓氏：

表1

表2记录了2021年中国人口最多的前12大姓氏：

表2

从《百家姓》开头的24大姓氏中随机选取1个姓氏，则这个姓氏是2021年中国人口最多的前12大姓氏的概率为______．

【答案】

【解析】

【分析】在年人口最多的前大姓氏中找出位于《百家姓》的前位的姓氏，并确定这些姓氏的数目，再利用古典概型的概率公式计算所求事件的概率．

【详解】年中国人口最多的前12大姓氏也是《百家姓》的前24大姓氏的是赵、李、周、吴、王、陈、杨、张、孙，共9个，故所求概率为

故答案为：.

15. 已知函数的图象关于直线对称，则___________．

【答案】##

【解析】

【分析】代入满足余弦函数对称轴的表达式，再根据求解即可

【详解】因为函数的图象关于直线对称，所以，即，又，所以．

故答案为：

16. 有一组样本数据，，…，如下表：

由这组数据得到新样本数据，，…，，其中，c为常数，则数据，，…，的方差为________．

【答案】

【解析】

【分析】先去掉样本数据，，…，的平均数和方差，再根据求解.

【详解】解：因为样本数据，，…，的平均数为，方差为．

所以数据，…，的方差为．

故答案为：

三、解答题：本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．

17. （1）若从区间内任意选取一个实数x，求的概率；

（2）从图中矩形（，图中的圆与和都相切）中任取一点P，求点P取自阴影部分的概率．

【答案】（1）；（2）

【解析】

【分析】（1）利用几何概型的概率公式直接求解，求出在内大于等于3的区间的长度，再除以区间的总长度即可，

（2）利用几何概型的概率公式直接求解，求出阴影部分的面积，再除以矩形的面积即可

【详解】（1）由几何概型可知，的概率为．

（2）由图可知，圆的直径为2，所以半径为1，

由几何概型可知，点P取自阴影部分的概率为．

18. 如图，在平行四边形中，．

（1）用表示；

（2）若，且，求．

【答案】（1），   

（2）

【解析】

【分析】（1）根据平面向量的加法和数乘运算，结合图形运算处理；（2）根据数量积的定义和运算律化简计算．

【小问1详解】

．

因为，所以，

所以．

【小问2详解】

因为，

所以

．

19. 某社区80名居民参加消防安全知识竞赛，竞赛后对其成绩（满分100分）进行统计，将数据按分为4组，其频率分布直方图如图所示．

（1）求直方图中a的值；

（2）试估计这80名居民竞赛成绩的平均分．（同一组中的数据用该组区间的中点值作代表）

【答案】（1）   

（2）84

【解析】

【分析】（1）由频率分布直方图中所有频率和为1可求得值；

（2）每组数据中点值乘以频率相加可得．

【小问1详解】

依题意得，，解得．

【小问2详解】

这80名居民竞赛成绩的平均分．

20. 已知函数的部分图象如图所示．

（1）求的解析式；

（2）若函数，求单调递增区间及在上的值域．

【答案】（1）   

（2）递增区间为，值域为

【解析】

【分析】（1）根据图象可确定振幅和周期，根据最低点可求，进而可得解析式；（2）根据整体代入的方式可求单调区间，根据的范围得，结合单调性即可求解最值，进而可得值域.

【小问1详解】

由图可知．

的最小正周期记为，则于，得．

因为，所以．

由，得．

即．

因为，所以，

所以．

【小问2详解】

由（1）可知，

由，

得，

则的单调递增区间为．

由，得，

则，

故在上的值域为．

21. 某产品的广告费用支出x（单位：万元）与销售额y（单位：万元）的数据如下表．

（1）在给出的坐标系中画出散点图；

（2）建立销售额关于广告费用支出的一元线性回归模型；

（3）利用所建立的模型，预测当广告费用支出为12万元时，销售额为多少．

（参考公式：线性回归方程中的系数，）

【答案】（1）见解析    （2）   

（3）107万元

【解析】

【分析】（1）根据表中数据直接描点即可；

（2）根据公式求出所要求的数据，分别求出，即可得出答案；

（2）根据回归方程，将代入即可得解.

【小问1详解】

解：如图所示，

【小问2详解】

解：，，

则，

，

所以，

则，

所以销售额关于广告费用支出的一元线性回归为；

【小问3详解】

解：由（2）得，当时，，

所以当广告费用支出为12万元时，销售额为万元.

22. 已知函数．

（1）若为钝角，且，求的值；

（2）若，均为锐角，且，求的取值范围．

【答案】（1）   

（2）

【解析】

【分析】（1）先利用二倍角的正切公式求出，再进行弦化切，代入求出的值；

（2）由求出，把消去，利用三角函数求最值

【小问1详解】

因为函数，为钝角，所以.

因为，所以，解得：（舍去）.

所以

把代入可得：

.

【小问2详解】

因为，所以，

所以，即.

因为，均为锐角，所以，所以，所以.

因为，所以，所以.

所以

因为，所以，所以，所以.

即的取值范围为.