2023年浙江省宁波市中考数学试卷（含解析）

这是一份2023年浙江省宁波市中考数学试卷（含解析），共25页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
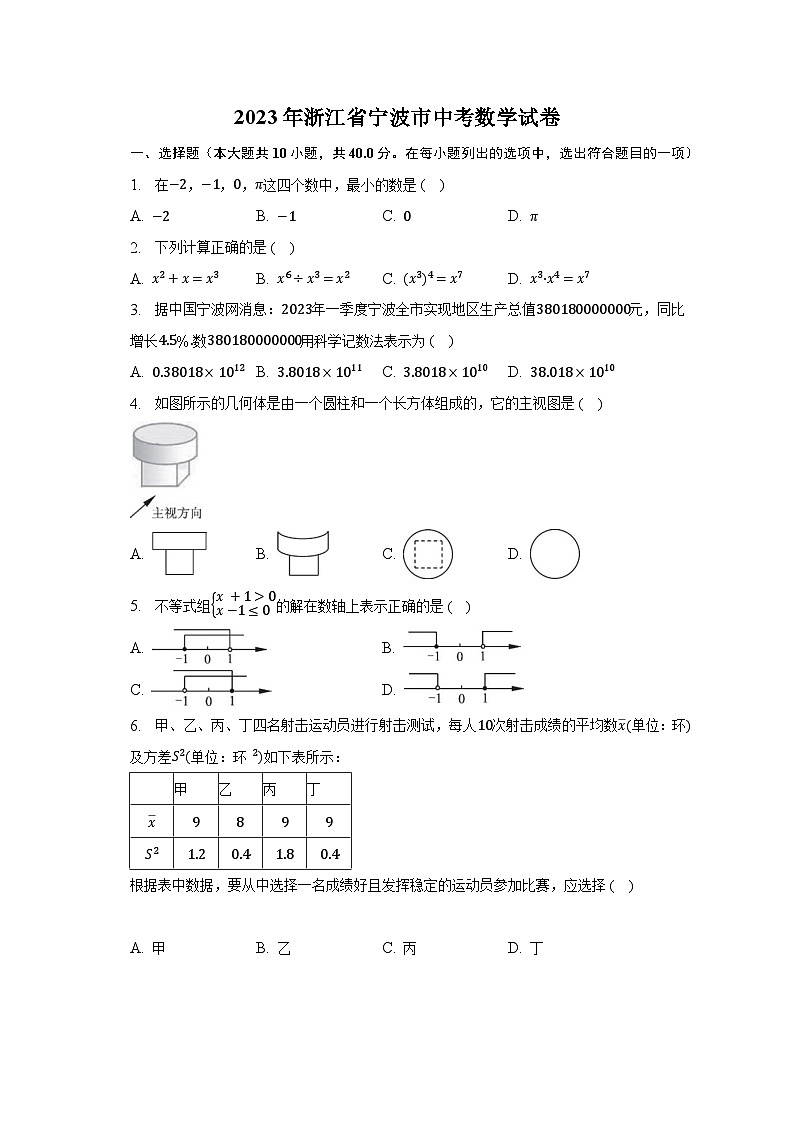
2023年浙江省宁波市中考数学试卷一、选择题（本大题共10小题，共40.0分。在每小题列出的选项中，选出符合题目的一项）1.  在，，，这四个数中，最小的数是(    )A.  B.  C.  D. 2.  下列计算正确的是(    )A.  B.  C.  D. 3.  据中国宁波网消息：年一季度宁波全市实现地区生产总值元，同比增长数用科学记数法表示为(    )A.  B.  C.  D. 4.  如图所示的几何体是由一个圆柱和一个长方体组成的，它的主视图是(    )
 A.  B.  C.  D. 5.  不等式组的解在数轴上表示正确的是(    )A.  B.
C.  D. 6.  甲、乙、丙、丁四名射击运动员进行射击测试，每人次射击成绩的平均数单位：环及方差单位：环如下表所示： 甲乙丙丁根据表中数据，要从中选择一名成绩好且发挥稳定的运动员参加比赛，应选择(    ) A. 甲 B. 乙 C. 丙 D. 丁7.  如图，一次函数的图象与反比例函数的图象相交于，两点，点的横坐标为，点的横坐标为，当时，的取值范围是(    )
 A. 或 B. 或
C. 或 D. 或8.  茶叶作为浙江省农业十大主导产业之一，是助力乡村振兴的民生产业．某村有土地公顷，计划将其中的土地种植蔬菜，其余的土地开辟为茶园和种植粮食．已知茶园的面积比种粮食面积的倍少公顷，问茶园和种粮食的面积各多少公顷？设茶园的面积为公顷，种粮食的面积为公顷，可列方程组为(    )A.  B.  C.  D. 9.  已知二次函数，下列说法正确的是(    )A. 点在该函数的图象上
B. 当且时，
C. 该函数的图象与轴一定有交点
D. 当时，该函数图象的对称轴一定在直线的左侧10.  如图，以钝角三角形的最长边为边向外作矩形，连接，，设，，的面积分别为，，，若要求出的值，只需知道(    )
 A. 的面积 B. 的面积
C. 的面积 D. 矩形的面积二、填空题（本大题共6小题，共30.0分）11.  分解因式：          ．12.  要使分式有意义，的取值应满足          ．13.  一个不透明的袋子里装有个绿球、个黑球和个红球，它们除颜色外其余相同．从袋中任意摸出一个球为绿球的概率为          ．14.  如图，圆锥形烟囱帽的底面半径为，母线长为，则烟囱帽的侧面积为          结果保留
 15.  如图，在中，，为边上一点，以为直径的半圆与相切于点，连接，， 是边上的动点，当为等腰三角形时，的长为          ．
 16.  如图，点，分别在函数 图象的两支上在第一象限，连接交轴于点点，在函数 图象上，轴，轴，连接，若，的面积为，四边形的面积为，则的值为          ，的值为          ．
 三、解答题（本大题共8小题，共80.0分。解答应写出文字说明，证明过程或演算步骤）17.  本小题分计算：．． 18.  本小题分在的方格纸中，请按下列要求画出格点三角形顶点均在格点上．在图中先画出一个以格点为顶点的等腰三角形，再画出该三角形向右平移个单位后的．将图中的格点绕点按顺时针方向旋转，画出经旋转后的．
 19.  本小题分如图，已知二次函数图象经过点和．求该二次函数的表达式及图象的顶点坐标．当时，请根据图象直接写出的取值范围． 20.  本小题分宁波象山作为杭州亚运会分赛区，积极推进各项准备工作．某校开展了亚运知识的宣传教育活动，为了解这次活动的效果，从全校名学生中随机抽取部分学生进行知识测试测试满分为分，得分均为不小于的整数，并将测试成绩分为四个等第：合格，一般，良好，优秀，制作了如下统计图部分信息未给出．
 由图中给出的信息解答下列问题：求测试成绩为一般的学生人数，并补全频数直方图．求扇形统计图中“良好”所对应的扇形圆心角的度数．这次测试成绩的中位数是什么等第？如果全校学生都参加测试，请你根据抽样测试的结果，估计该校测试成绩为良好和优秀的学生共有多少人？ 21.  本小题分某综合实践研究小组为了测量观察目标时的仰角和俯角，利用量角器和铅锤自制了一个简易测角仪，如图所示．如图，在点观察所测物体最高点，当量角器零刻度线上，两点均在视线上时，测得视线与铅垂线所夹的锐角为，设仰角为，请直接用含的代数式表示．如图，为了测量广场上空气球离地面的高度，该小组利用自制简易测角仪在点，分别测得气球的仰角为，为，地面上点，，在同一水平直线上，，求气球离地面的高度参考数据：，，

  22.  本小题分某校与部队联合开展红色之旅研学活动，上午，部队官兵乘坐军车从营地出发，同时学校师生乘坐大巴从学校出发，沿公路如图到爱国主义教育基地进行研学．上午，军车在离营地的地方追上大巴并继续前行，到达仓库后，部队官兵下车领取研学物资，然后乘坐军车按原速前行，最后和师生同时到达基地．军车和大巴离营地的路程与所用时间的函数关系如图所示．求大巴离营地的路程与所用时间的函数表达式及的值．求部队官兵在仓库领取物资所用的时间． 23.  本小题分定义：有两个相邻的内角是直角，并且有两条邻边相等的四边形称为邻等四边形，相等两邻边的夹角称为邻等角．如图，在四边形中，，，对角线平分求证：四边形为邻等四边形．如图，在的方格纸中，，，三点均在格点上，若四边形是邻等四边形，请画出所有符合条件的格点．如图，四边形是邻等四边形，，为邻等角，连接，过作交的延长线于点若，，求四边形的周长．

  24.  本小题分如图，锐角内接于，为的中点，连接并延长交于点，连接，，过作的垂线交于点，点在上，连接，，若平分且．求的度数．求证：．若，求的值．如图，当点恰好在上且时，求的长．

答案和解析 1.【答案】 【解析】【分析】
根据负数小于小于正数，负数的绝对值大的反而小，进行判断即可．
本题考查比较实数的大小．熟练掌握负数小于，小于正数，负数的绝对值大的反而小，是解题的关键．
【解答】
解：，
，
最小的数是；
故选．   2.【答案】 【解析】【分析】
根据同底数幂的乘法、除法，幂的乘方，合并同类项进行运算，然后判断即可．
本题考查了同底数幂的乘法、除法，幂的乘方，合并同类项．解题的关键在于正确的运算．
【解答】
解：、，错误，故不符合要求；
、，错误，故不符合要求；
、，错误，故不符合要求；
、，正确，故符合要求；
故选．  3.【答案】 【解析】【分析】
用科学记数法表示绝对值较大的数时，一般形式为，其中，为整数，且比原来的整数位数少，据此判断即可．
此题主要考查用科学记数法表示绝对值较大的数，一般形式为，其中，确定与的值是解题的关键．
【解答】
解：，共有位数字， 
，
故选．  4.【答案】 【解析】【分析】
根据几何体的主视图的含义可直接进行判断．
本题主要考查几何体的三视图，熟练掌握几何体的三视图的画法是解题的关键．
【解答】
解：由题意可得：该几何体的主视图为
，
故选A．  5.【答案】 【解析】【分析】
根据一元一次不等式组的解法先求出不等式组的解集，再在数轴上表示即可得到答案．
本题考查一元一次不等式组解集的求法及在数轴上的表示，熟练掌握不等式组解集的求解原则“同
大取大、同小取小、大小小大中间找、大大小小无解了”是解决问题的关键．
【解答】
解：，
由得
由得
原不等式组的解集为，
在数轴上表示该不等式组的解集为：，
故选C．  6.【答案】 【解析】【分析】
根据次射击成绩的平均数可淘汰乙；再由次射击成绩的方差可知，
也就是丁的射击成绩比较稳定，从而得到答案．
本题考查通过统计数据做决策，熟记平均数与方差的定义与作用是解决问题的关键．
【解答】
解：，
由四人的次射击成绩的平均数可淘汰乙
，
由四人的次射击成绩的方差可知丁的射击成绩比较稳定
故选D．  7.【答案】 【解析】【分析】
根据不等式与函数图像的关系，当时，的取值范围是指反比例函数在一次函数上方图像对应的的取值范围，数形结合即可得到答案．
本题考查由函数图像解不等式，熟练掌握不等式与函数图像的关系是解决问题的关键．
【解答】
解：由图可知，一次函数的图像与反比例数的图像相交于，两点，点的横坐标为，点的横坐标为，
当或时，有反比例函数图像在一次函数图像上方，
即当时，的取值范围是或，
故选：．  8.【答案】 【解析】【分析】
根据某村有土地公顷，计划将其中的土地种植蔬菜，得到种植茶园和种植粮食的面积为公顷，结合茶园的面积比种粮食面积的倍少公顷，列出方程组即可．
本题考查根据实际问题列方程组，找准等量关系，正确的列出方程组，是解题的关键．
【解答】
解：设茶园的面积为公顷，种粮食的面积为公顷，
由题意，得：
化简：
故选B．  9.【答案】 【解析】【分析】
根据二次函数的图象和性质，逐一进行判断即可．
本题考查二次函数的图象和性质，熟练掌握二次函数的性质，是解题的关键．
【解答】
解：，
当时，，
，
，
即点不在该函数的图象上，故A选项错误；
当时，，
抛物线的开口向上，对称轴为，
抛物线上的点离对称轴越远，函数值越大，
，，
当时，有最大值为，
当时，有最小值为，
，故B选项错误
，
该函数的图象与轴一定有交点，故选项C正确
当时，抛物线的对称轴为：，
该函数图象的对称轴一定在直线的右侧，故选项D错误
故选C．  10.【答案】 【解析】【分析】
过点作，交的延长线于点，的延长线于点，易得：
，，，利用矩形的性质和三角形的面积公式，可得，再根
据，得到，即可得出结论．
本题考查矩形的性质，求三角形的面积，解题的关键是得到．
【解答】
解：过点作，交的延长线于点，的延长线于点，

四边形是矩形，
，，，
，，
四边形为矩形，
，，，
，，
，
又，
，
只需要知道的面积即可求出的值
故选C．  11.【答案】  【解析】【分析】
因为是两个数的平方差，所以利用平方差公式分解即可．
本题考查了平方差公式因式分解，熟记平方差公式的特点：两项平方项，符号相反，是解题的关键．
【解答】
 解：，
  故答案为．  12.【答案】 【解析】【分析】
根据分式有意义的条件：分母不为零，从而得到，求解即可得到答案．
本题考查分式有意义的条件，熟记分式有意义的条件：分母不为零是解决问题的关键．
【解答】
 解：要使分式有意义，的取值应满足，解得，
故答案为．  13.【答案】 【解析】【分析】
从袋子里任意摸一个球有种等可能的结果，其中是绿球的有种，根据简单概率公式代值求解即可得到答案．
本题考查概率问题，弄清总的结果数及符合要求的结果数，熟记简单概率公式求解是解决问题的关键．
【解答】
解：由题意可知，从袋子里任意摸一个球有种等可能的结果，其中是绿球的有种，
任意摸出一个球为绿球，
故答案为．  14.【答案】 【解析】【分析】
根据圆锥侧面展开图是一个扇形，由扇形面积公式代值求解即可得到答案．
本题考查圆锥侧面展开图及扇形面积公式，熟记扇形面积公式是解决问题的关键．
【解答】
解：圆锥形烟囱帽的底面半径为，母线长为，
烟囱帽的侧面积，
故答案为．  15.【答案】或 【解析】【分析】
连接，由勾股定理求出半径，平行线分线段成比例，求出的长，再由勾股定理求出和的长，分和两种情况进行求解即可．
本题考查切线的性质，平行线分线段成比例，勾股定理，等腰三角形的定义熟练掌握切线的性质，等腰三角形的定义，确定点的位置，是解题的关键．
【解答】
解：连接，

以为直径的半圆与相切于点，
，，

设，则，
在中：，即：，
解得：，
，
，，，
，
，
，
，
，
，
，

为等腰三角形，
当时，，
当时，
，
点与点重合，
，

不存在的情况
综上：的长为或．
故答案为或．  16.【答案】 【解析】【分析】
如图，延长，交于点，与轴交于点，而轴，轴，可得，由的面积为，四边形的面积为，可得的面积是，设，，则，，，利用面积可得，，由，，可得，可得，再利用方程思想解题即可．
本题考查的是反比例函数的几何应用，平行线分线段成比例的应用，坐标与图形面积，熟练的利用方程思想解题是关键．
【解答】
解：如图，延长，交于点，与轴交于点，而轴，轴，
，
的面积为，四边形的面积为，
的面积是，

设，，
，，，
，，，，
，，
整理得：，，
，，
，
，
，则，
把代入得：，
，即，
把代入得：，
把代入得：
故答案为．  17.【答案】解：




． 【解析】根据零指数幂运算、去绝对值运算和算术平方根运算分别求解，再利用有理数加减运算求解即可得到答案
根据平方差公式、单项式乘以多项式将原式展开，合并同类项即可得到答案．
本题考查实数混合运算及整式混合运算，熟记相关运算法则是解决问题的关键．
 18.【答案】解：如图，，即为所求作的三角形答案不唯一

如图，即为所求作的三角形，
 【解析】先画等腰三角形，再确定平移后的对应点，再顺次连接即可
确定，旋转后的对应点，而的对应点是其本身，再顺次连接即可．
本题考查的是平移，旋转的作图，作等腰三角形，熟练的利用网格特点以及平移旋转的性质进行作图是解本题的关键．
 19.【答案】二次函数图象经过点和．
，解得：
二次函数的表达式为，
函数图象的顶点坐标为．
 【解析】解：见答案；
当时，，

解得：，，

如图，当时，
故的取值范围为
把和代入，建立方程组求解解析式即可，再把解析式化为顶点式，可得顶点坐标
把代入函数解析式求解的值，再利用函数图象可得时的取值范围．
本题考查的是利用待定系数法求解二次函数的解析式，二次函数的顶点坐标，利用图象法解不等式，熟练的运用数形结合的方法解题是关键．

 20.【答案】解：人，
测试成绩为一般的学生人数为：人
补全直方图如图：

“良好”所对应的扇形圆心角：
共人，将成绩按照从小到大排序后，第个数据和第个数据均在的范围内，即中位数的等第是良好
人
答：估计该校测试成绩为良好和优秀的学生共有人． 【解析】利用优秀的人数除以所占的百分比求出总数，利用总数减去其他等级的人数求出测试成绩为
一般的学生人数，进而补全直方图即可
良好等级的人数所占的比例进行计算即可
利用中位数的定义进行作答即可
利用总体乘以样本中测试成绩为良好和优秀的学生所占的比例，即可得解．
本题考查统计图，中位数，利用样本估计总体从统计图中有效的获取信息，熟练掌握中位数的计算方法，是解题的关键．
 21.【答案】解：如图所示：

由题意知，
在中，，则，即，

如图所示：

，
在中，，由等腰直角三角形性质得到，
在中，，
由，
即，
解得，
气球离地面的高度为． 【解析】如图所示，铅垂线与水平线相互垂直，从而利用直角三角形中两锐角互余即可得到答案
根据题意，，在中，，由等腰直角三角形性质得到在中，，由 ，解方程即可得到答案．
本题考查解直角三角形的实际应用，涉及直角三角形性质、等腰直角三角形性质等，熟练掌握解直角三角形的方法及相关知识点是解决问题的关键．
 22.【答案】解：设大巴离营地的路程与所用时间的函数表达式为，由图象可知，直线过点，，
，解得：，

当时，，解得：，

由图象可知，军车的速度为：，
军车到达仓库所用时间为：，
从仓库到达基地所用时间为：，
部队官兵在仓库领取物资所用的时间为 【解析】设出函数解析式，利用待定系数法求出函数解析式，将，代入解析式求出的值即可
先求出军车的速度，然后分别求出军车到达仓库，和从仓库出发到达基地的时间，用总时间减去两段
时间即可得解．
本题考查一次函数的实际应用，从函数图象上有效的获取信息，正确的求出函数解析式，是解题的关键．
 23.【答案】解：，，
，，
对角线平分，
，
，
，
四边形为邻等四边形．
如图，，，即为所求

如图，过作于，

，
四边形是矩形，
，，，
，
四边形为平行四边形，
，，
设，而，
，，
由新定义可得，
在中，，
在中，

 ，
整理得：，
解得：，不符合题意舍去，
，
四边形的周长为． 【解析】先证明，，再证明，即可得到结论
根据新定义即可得，再确定，，的格点即可
如图，过作于，可得四边形是矩形，，，证明四边形为平行四边形，可得，，设，而，，，由新定义可得，由勾股定理可得：，再解方程可得答案．
本题考查的是新定义的含义，平行线的性质，等腰三角形的判定，平行四边形的判定与性质，矩形的判定与性质，勾股定理的应用，一元二次方程的解法，理解题意，作出合适的辅助线是解本题的关键．
 24.【答案】证明：平分，
，
，
，

，
，
，
，
．
为中点，，
，
，
，
，
，
，，
，
．
设，，
，，
，，
∽，
，即，
，即，
，
，
负根舍去
如图，设的半径为，连接交于，过作于，

，
，
，
，，
，
，
，
，而，，
，
，
，
，
，
∽，
，即，
解得：，负根舍去，
． 【解析】先证明，结合，，可得，从而可得答案
证明，再证明，可得设，，证明
∽，可得，即，则，可得
，从而可得答案
如图，设的半径为，连接交于，过作于，证明，，可得，证明，可得，，证明∽，，即，再解方程可得答案．
本题考查的是全等三角形的判定与性质，相似三角形的判定与性质，圆的基本性质，圆周角定理的应用，垂径定理的应用，求解锐角的正切，本题的难度大，作出合适的辅助线是解本题的关键．