2023年河南省信阳市光山县孙铁铺中学中考数学三模试卷（含解析）

2023年河南省信阳市光山县孙铁铺中学中考数学三模试卷

一、选择题（本大题共10小题，共30.0分。在每小题列出的选项中，选出符合题目的一项）

1.  对于，第一个因数增加后积的变化是(    )

A. 增加 B. 减少 C. 增加 D. 减少

2.  从一台对讲机发出无线电信号到外的另一台对讲机接收到该信号，大约需要，用科学记数法表示外的一台对讲机接收到该信号大约需要(    )

A.  B.  C.  D.

3.  下列每个几何体均由六个相同的小正方体搭成，其中与如图所示的几何体主视图相同的是(    )

A.
B.
C.
D.

4.  下列计算结果为的是(    )

A.  B.  C.  D.

5.  如图，，若，，则的度数是(    )

A.
B.
C.
D.

6.  如图，数轴上，与表示的点分别为、、，点为线段上一点，分别以、为中心旋转、，若旋转后、两点可以重合成一点即构成，则点代表的数可能为(    )

A.  B.  C.  D.

7.  将二次函数的图象向右平移个单位长度，再向下平移个单位长度得到的二次函数解析式是
(    )

A.  B.  C.  D.

8.  定义运算：，如，则方程根的情况是(    )

A. 有两个不相等的实数根 B. 有两个相等的实数根
C. 只有一个实数根 D. 无实数根

9.  如图，正方形中，点，点为上一点，且，连接，过点作交于点，过点作，交轴于点，交于点，则点的坐标为(    )

A.  B.  C.  D.

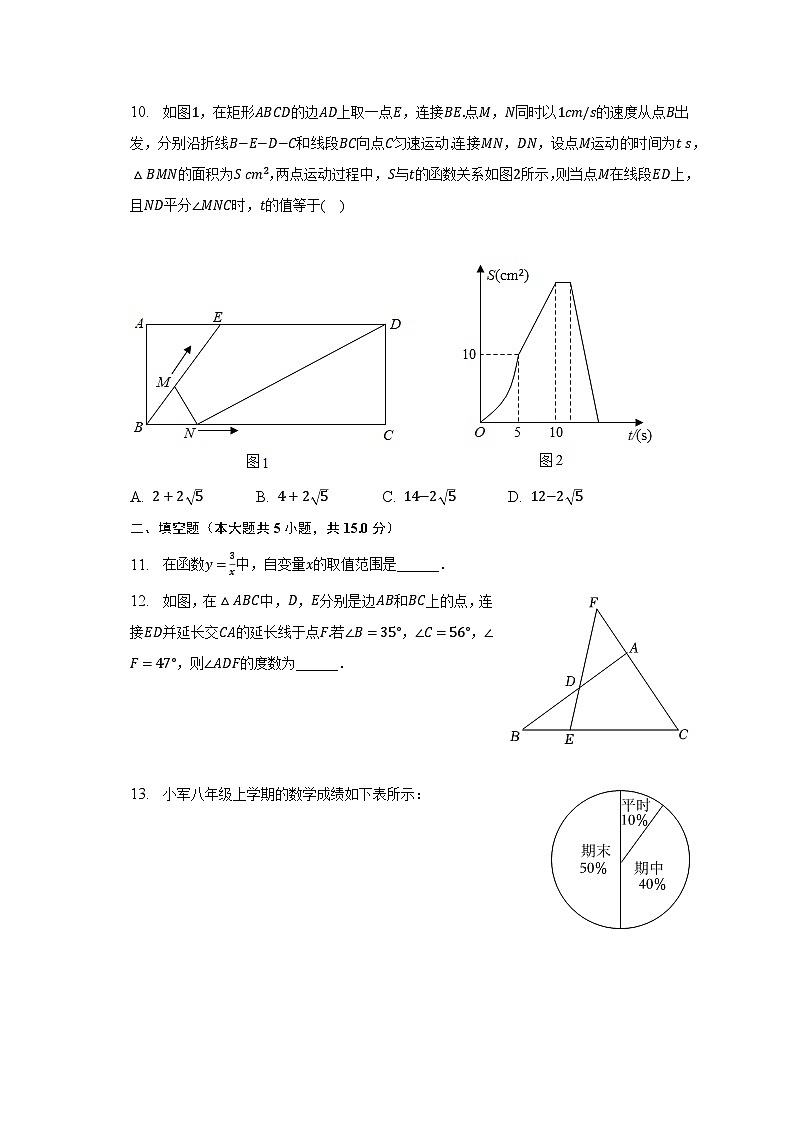
10.  如图，在矩形的边上取一点，连接点，同时以的速度从点出发，分别沿折线和线段向点匀速运动连接，，设点运动的时间为，的面积为，两点运动过程中，与的函数关系如图所示，则当点在线段上，且平分时，的值等于(    )

 

A.  B.  C.  D.

二、填空题（本大题共5小题，共15.0分）

11.  在函数中，自变量的取值范围是______．

12.  如图，在中，，分别是边和上的点，连接并延长交的延长线于点若，，，则的度数为______．

13.  小军八年级上学期的数学成绩如下表所示：

如果学期总评成绩按图所示的扇形图的权重计算图中“平时”指平时各次成绩的算术平均数，则小军上学期的总评成绩是______ 分

14.  如图，在平行四边形中，，，，为上一点，以点为圆心，长为半径画弧，交于点，若，则图中阴影部分的面积为______ 结果保留．

15.  如图，在中，，，，点为边的中点，点为边上一动点，连接，作关于直线的轴对称图形，点的对应点为点，连接，则长度的取值范围为______．

三、解答题（本大题共7小题，共65.0分。解答应写出文字说明，证明过程或演算步骤）

16.  本小题分
计算：；
解不等式组：．

17.  本小题分
某校七、八年级各有名学生，为了解该校七、八年级学生对党史知识的掌握情况，从七、八年级学生中各随机抽取人进行党史知识测试，统计这部分学生的测试成绩成绩均为整数，满分分，分及分以上为优秀，相关数据统计整理如下：
七年级抽取学生的成绩：，，，，，，，，，，，，，，．
七、八年级抽取学生的测试成绩统计表

填空：______，______．
根据以上数据，你认为该校七、八年级中，哪个年级的学生党史知识掌握得较好？请说明理由写出一条即可．
请估计七、八年级学生对党史知识掌握能够达到优秀的总人数；
现从七、八年级获得分的名学生中随机抽取人参加市党史知识竞赛，请用列表法或画树状图法，求出被选中的人恰好是七、八年级各人的概率．

18.  本小题分
九龙鼎是洛阳的一座标志性建筑，代表东周、东汉、魏、西晋、北魏、隋、唐、后梁、后唐等个朝代在这里建都．如图，某中学九年级数学兴趣小组想测量九龙鼎的高度，小明在九龙鼎前的一座写字楼的处仰望顶端，测得仰角为，小亮在写字楼前处，测得九龙鼎的顶端的仰角为，点，，在同一条直线上，米，米，求九龙鼎的高度．
参考数据；，，，
 

19.  本小题分
临近期末，某文具店需要购进一批涂卡铅笔和黑色水笔，已知用元购进铅笔与用元购进水笔的数量相同，且每支铅笔比每支水笔进价高元．
求这两种笔每支的进价分别是多少元？
该商店计划购进水笔的数量比铅笔数量的倍还多支，且两种笔的总数量不超过支，售价见店内海报如下所示该商店应如何安排进货才能使利润最大？最大利润是多少？

20.  本小题分
如图，是的外接圆，是的直径，是的切线，切点为，，连接交于，连接．
证明：平分；
作的角平分线交于点，尺规作图，保留作图痕迹，不写作法
若，，求的值．

21.  本小题分
共享电动车是一种新理念下的交通工具：主要面向的出行市场，现有、两种品牌的共享电动车，收费与骑行时间之间的函数关系如图所示，其中品牌收费方式对应，品牌的收费方式对应．
求品牌的函数关系式；
如果小明每天早上需要骑行品牌或品牌的共享电动车去工厂，上班，已知两种品牌共享电动车的平均行驶速度均为，小明家到工厂的距离为，那么小明选择哪个品牌的共享电动车更省钱呢？
直接写出两种收费相差元时的值．

22.  本小题分
在平面直角坐标系中，直线与轴、轴分别交于点、如图抛物线经过点．
求线段的长；
如果抛物线经过线段上的另一点，且，求这条抛物线的表达式；
如果抛物线的顶点位于内，求的取值范围．

答案和解析

1.【答案】 

【解析】解：，
第一个因数增加后积为：，
，
积的变化是：增加，
故选：．
根据因数因数积，可得当第一个因数增加时，积增加，据此判断即可．
本题考查了有理数乘法问题的应用，注意灵活应用因数和积的关系解答即可．
 

2.【答案】 

【解析】解：，
故选：．
科学记数法的表示形式为的形式，其中，为整数．确定的值时，要看把原数变成时，小数点移动了多少位，的绝对值与小数点移动的位数相同．当原数绝对值时，是正整数；当原数的绝对值小于时，是负整数．
此题考查科学记数法的表示方法．科学记数法的表示形式为的形式，其中，为整数，表示时关键要确定的值以及的值．
 

3.【答案】 

【解析】解：的主视图为：，
A、主视图为，主视图不同，故此选项不合题意；
B、主视图为，主视图不同，故此选项不合题意；
C、主视图为，主视图相同，故此选项符合题意；
D、主视图为，主视图不同，故此选项不合题意；
故选：．
分别画出四个选项中简单组合体的三视图即可．
此题主要考查了简单组合体的三视图，关键是掌握左视图和主视图的画法．
 

4.【答案】 

【解析】解：、，故A不符合题意；
B、，故B符合题意；
C、，故C不符合题意；
D、与不属于同类项，不能合并，故D不符合题意．
故选：．
利用合并同类项的法则，同底数幂的除法的法则对各项进行运算即可．
本题主要考查合并同类项，同底数幂的除法，解答的关键是对相应的运算法则的掌握．
 

5.【答案】 

【解析】解：，，
，
，
．
故选：．
由可求出，再根据两直线平行，同位角相等即可求解．
本题主要考查平行线的性质，熟记平行线的性质定理是解题关键．平行线性质定理：定理：两条平行线被第三条直线所截，同位角相等．简单说成：两直线平行，同位角相等．定理：两条平行线被第三条直线所截，同旁内角互补．简单说成：两直线平行，同旁内角互补．定理：两条平行线被第三条直线所截，内错角相等．简单说成：两直线平行，内错角相等．
 

6.【答案】 

【解析】解：可设表示的数为，，
则，，
中，；，
，
，
，
故选：．
利用两点间的距离，三边关系，推出第三边条的取值范围即可．
本题考查的数轴上的点表示的数，解题的关键是熟练掌握三角形三边关系．
 

7.【答案】 

【解析】解：将二次函数的图象向右平移个单位长度，再向下平移个单位长度得到的二次函数解析式是，即．
故选：．
按照“左加右减，上加下减”的规律进而求出即可．
此题考查了抛物线的平移以及抛物线解析式的变化规律：左加右减，上加下减．
 

8.【答案】 

【解析】解：根据题中的新定义得：，
整理得：，
，
方程没有实数根．
故选：．
方程利用题中的新定义化简，计算出根的判别式的值，即可作出判断．
此题考查了根的判别式，实数的运算，弄清题中的新定义是解本题的关键．
 

9.【答案】 

【解析】解：是正方形，，
，，
，
，，
，
，
在和中，
，
≌，
，
，
设直线为，把，代入得：
，解得，
直线为，
由设直线为，把代入得：
，
解得，
直线为，
在中，令得，
解得，
，
故选：．
由是正方形，，得，，又，知，，根据，可证明≌，即知，，设直线为，用待定系数法可得直线为，根据设直线为，可得直线为，令即可得．
本题考查正方形与一次函数综合应用，解题的关键是求出的坐标，从而得出直线的解析式．
 

10.【答案】 

【解析】解：图中，当点移到点时，对应图中的点，同时点也到点，
即线段和用时秒，而点移动速度是，则，

图中，当点从点到时，对应图中从点到点，用时秒，
同时点从到，点对应点，用时秒，故E，
，解得，
当移到时，平分，
则，
在中，，，得，又，
在中，，，得，
所以，
在中，，
，，
，
，
当点在线段上，且平分时，的值等于秒，
故选：．
观察点的移动轨迹，确定出图和图的对应点：，，，，
观察点的移动轨迹，确定出图和图的对应点：，，，
依次求出，，长度都为；，解得，即，也是，
作出，点，使得平分，利用的面积公式，解得，，，即为所求．
本题考查动点在矩形中运动，其过程轨迹和函数图象相结合，重点是找出点的运动过程在函数图象的一些关键点，难点是画出角平分线求出D.
 

11.【答案】 

【解析】解：由题意得：
，
故答案为：．
根据分母不为，即可解答．
本题考查了函数自变量的取值范围，熟练掌握分母不为是解题的关键．
 

12.【答案】 

【解析】解：是的外角，，，
，
，
．
故答案为：．
由三角形的外角性质可求得，再利用三角形的内角和即可求的度数．
本题主要考查三角形的外角性质，三角形的内角和定理，解答的关键是熟记三角形的外角性质及三角形的内角和定理．
 

13.【答案】 

【解析】解：平时平均成绩为：分．
学期总评成绩为：分．
故答案为：．
从表格中得出数据，先计算平时平均成绩，再根据加权平均数计算学期总评成绩．
本题考查了扇形统计图和加权平均数，牢记公式是解答本题的关键．
 

14.【答案】． 

【解析】解：如图，连接，

，，，
，，，
，
是等边三角形，
，
，
四边形是平行四边形，
，，
，


．
故答案为：．
连接，先通过直角三角形的性质可得，长，，结合可得是等边三角形，进而可得、的长，再利用平行四边形的性质可得的面积，的度数，最后利用计算即可．
本题主要考查扇形面积的计算、直角三角形的性质、平行四边形的性质，解题关键是将不规则面积转化成规则面积．
 

15.【答案】 

【解析】解：如图，连接．

在中，，，，
，
，
，
由对称的性质可知，，
，
的最小值为，
当点与重合时，的值最大，此时，，

．
故答案为：．
如图，连接求出，根据，推出的最小值为，当点与重合时，的值最大，求出的最大值，可得结论．
本题考查翻折变换，解直角三角形等知识，解题的关键是求出的最小值与最大值，属于中考常考题型．
 

16.【答案】解：



；
，
解不等式，得：，
解不等式，得：，
故原不等式组的解集是． 

【解析】先算括号内的式子，然后计算括号外的除法即可；
先解出每个不等式的解集，即可得到不等式组的解集．
本题考查分式的混合运算、解一元一次不等式组，熟练掌握运算法则和解一元一次不等式的方法是解答本题的关键．
 

17.【答案】解：由众数的定义得：，
八年级抽取学生的测试成绩的中位数为分，
故答案为：，；
七年级的学生党史知识掌握得较好，理由如下：
七年级的优秀率大于八年级的优秀率，
七年级的学生党史知识掌握得较好；
人，
即估计七、八年级学生对党史知识掌握能够达到优秀的总人数为人；
七年级有位学生的成绩为分，八年级有位学生的成绩是分，
把七年级获得分的学生记为，八年级获得分的学生记为，
画树状图如图：

共有种等可能的结果，被选中的人恰好是七、八年级各人的结果有种，
被选中的人恰好是七、八年级各人的概率为． 

【解析】由众数和中位数的定义求解即可；
七、八年级的平均数和中位数相同，七年级的优秀率大于八年级的优秀率，即可求解；
由七、八年级的总人数分别乘以优秀率，再相加即可；
画树状图，共有种等可能的结果，被选中的人恰好是七、八年级各人的结果有种，再由概率公式求解即可．
本题考查了列表法与树状图法、条形统计图、统计表、中位数、众数等知识；利用列表法或树状图法展示所有等可能的结果，再从中选出符合事件或的结果数目，然后利用概率公式计算事件或事件的概率．
 

18.【答案】解：过点作于点．

则米，，，，
设米，则米，
在中，，
米，
米，
在中，
，
解得，
九龙鼎的高度约为米． 

【解析】过点作于点，则米，，，，设米，则米，在中，，则米，可得米，在中，，求解即可．
本题考查解直角三角形的应用仰角俯角问题，熟练掌握锐角三角函数的定义是解答本题的关键．
 

19.【答案】解：设每支黑色水笔的进价为元，则每支涂卡铅笔的进价为元，
依题意得：，
解得：，
经检验，是原方程的解，且符合题意，
．
答：每支涂卡铅笔的进价为元，每支黑色水笔的进价为元．
设购进支涂卡铅笔，则购进支黑色水笔，
依题意得：，
解得：．
设购进的这批笔全部售出后获得的总利润为元，则，
，
随的增大而增大，
当时，取得最大值，最大值，此时．
答：该商店应购进支涂卡铅笔，支黑色水笔才能使利润最大，最大利润是元． 

【解析】设每支黑色水笔的进价为元，则每支涂卡铅笔的进价为元，利用数量总价单价，结合用元购进铅笔与用元购进水笔的数量相同，即可得出关于的分式方程，解之经检验后即可得出每支黑色水笔的进价，再将其代入中即可求出每支涂卡铅笔的进价；
设购进支涂卡铅笔，则购进支黑色水笔，根据购进两种笔的总数量不超过支，即可得出关于的一元一次不等式，解之即可求出的取值范围，设购进的这批笔全部售出后获得的总利润为元，利用总利润每支笔的销售利润销售数量购进数量，即可得出关于的函数关系式，再利用一次函数的性质，即可解决最值问题．
本题考查了分式方程的应用、一元一次不等式的应用以及一次函数的应用，解题的关键是：找准等量关系，正确列出分式方程；根据各数量之间的关系，找出关于的函数关系式．
 

20.【答案】证明：连接，
是的切线，
，
，
，
，
，
平分；

如图：即是的角平分线；

解：，，且，，
，
，
公共角，，
∽，
：：，
，
是的直径，
，
． 

【解析】首先连接，由是的切线，切点为，，易证得，然后由垂径定理，求得平分；
根据角平分线的作法，求解即可求得的角平分线；
易证得是等腰三角形，即可求得的长，∽，然后由相似三角形的对应边成比例，求得的长，继而求得答案．
此题考查了切线的性质，角平分线的作法、等腰三角形的判定与性质、相似三角形的判定与性质、垂径定理、圆周角定理以及三角函数的性质．此题难度适中，注意掌握辅助线的作法，注意数形结合思想的应用．
 

21.【答案】解：由图象可知，当时，，
当时，设，
把点和点代入中，
得：，
解得：，
，
；
，，
，
由图象可知，当骑行时间不足时，
，即骑行品牌的共享电动车更省钱．
小明选择品牌的共享电动车更省钱；
当时两种收费相同，
两种收费相差元，分前和后两种情况，
当时，离越近收费相差的越少，
当时，，
，
，
要使两种收费相差元，应小于，
，
解得：；
当时，，
解得：．
在分钟或分钟，两种收费相差元． 

【解析】根据图像可知，品牌的函数关系式分两段求解．利用待定系数法求函数解析式即可；
先求出小明从家到工厂所用时间为，再通过图像可知小于时选择品牌电动车更省钱；
分两种情况讨论，，分别解方程即可．
本题考查了一次函数的图象、待定系数法求一次函数解析式以及解一元一次方程，解题的关键是观察函数图象，找出点的坐标，利用待定系数法求出函数关系式．
 

22.【答案】解：针对于直线，
令，，
，
令，则，
，
，
；

设点，
，
，
，
，
，
点在线段上，
，
，
将点，代入抛物线中，得，
，
抛物线；

点在抛物线中，得，
，
抛物线的解析式为，
抛物线的顶点坐标为，
将代入中，得，
顶点位于内，
，
； 

【解析】先求出，坐标，即可得出结论；
设点，则，进而求出点，最后将点，代入抛物线解析式中，即可得出结论；
将点坐标代入抛物线解析式中得出，代入抛物线解析式中得出顶点坐标为，即可得出结论．
此题是二次函数综合题，主要考查了待定系数法，两点间的距离公式，抛物线的顶点坐标的求法，求出点的坐标是解本题的关键．