2023年河北省石家庄市第四十八中学（原第二中学南校区）中考模拟数学试题（6月）（含答案）

2023年九年级中考模拟练习内测试题

数学试卷

注意事项：

1．本试卷共8页，总分120分，考试时间120分钟．

2．答题前，考生务必将姓名、准考证号填写在试卷和答题卡相应位置上．

3．考生务必将答案写在答题卡上，写在本试卷上无效．

4．考试结束后，将本试卷和答题卡一并交回．

一、选择题（本大题有16个小题，共42分．1～10小题各3分；11～16小题各2分，在每小题给出的四个选项中，只有一项是符合题目要求的）

1．若分式的值为零，则的值是（    ）

A．1 B．－1 C． D．2

2．下列各组数中，把两数相乘，积为1的是（    ）

A．2和－2 B．－2和 C．和 D．和

3．若，，则ab等于（    ）

A．1 B．2 C．－2 D．－1

4．下面是一位同学做的四道题：①；②；③；④．其中做对的一道题的序号是（    ）

A．① B．② C．③ D．④

5．如图，将平形四边形纸片沿着线段尊成两个全等的图形，则的度数是（    ）

A． B． C． D．

6．将一次函数的图象沿轴向右平移2个单位长度，得到的函数解析式是（    ）

A． B． C． D．

7．若关于的一元二次方程有两个不相等的实数根，则实数的取值范围是（    ）

A． B．且 C． D．或

8．一个不透明的袋子中有2个白球，3个黄球和1个红球，这些球除颜色不同外其他完全相同，则从袋子中随机摸出一个球是白球的概率为（    ）

A． B． C． D．

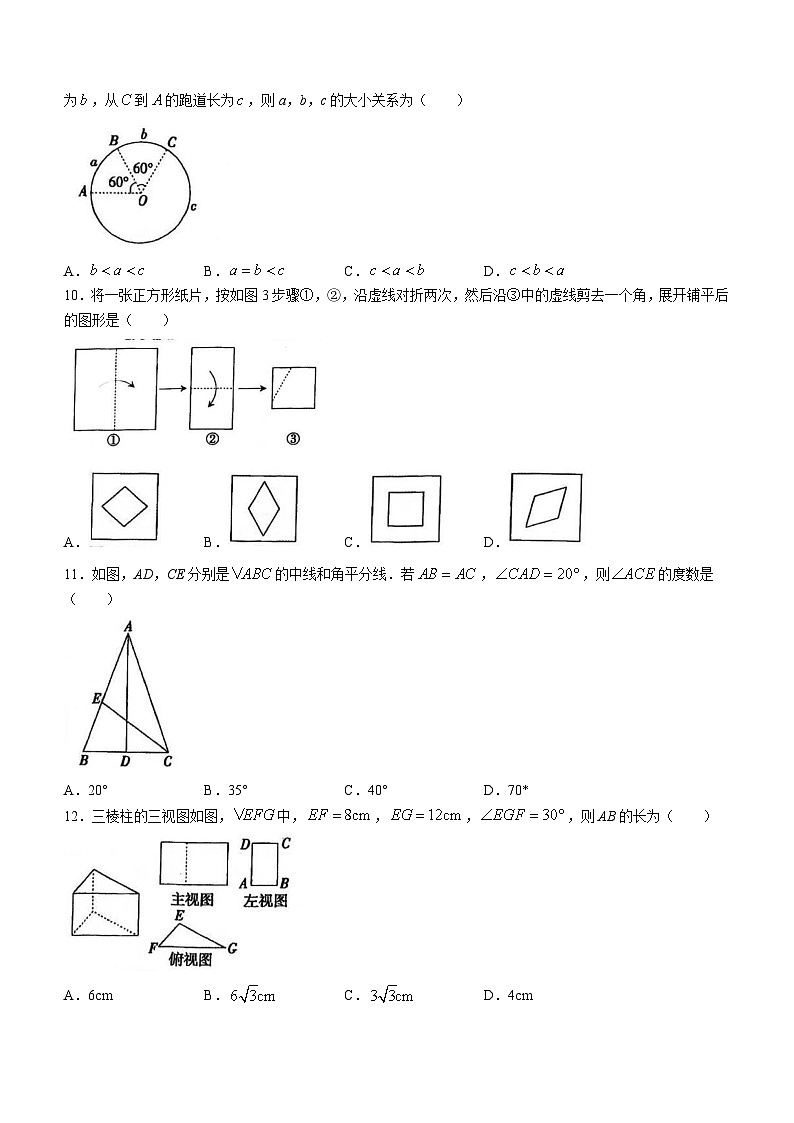
9．如图，以为圆心的圆形跑道上，有三个起点A，B，C，设从到的跑道长为，从到的跑道长为，从到的跑道长为，则a，b，c的大小关系为（    ）

A． B． C． D．

10．将一张正方形纸片，按如图3步骤①，②，沿虚线对折两次，然后沿③中的虚线剪去一个角，展开铺平后的图形是（    ）

A． B． C． D．

11．如图，AD，CE分别是的中线和角平分线．若，，则的度数是（    ）

A．20° B．35° C．40° D．70*

12．三棱柱的三视图如图，中，，，，则AB的长为（    ）

A．6cm B． C． D．4cm

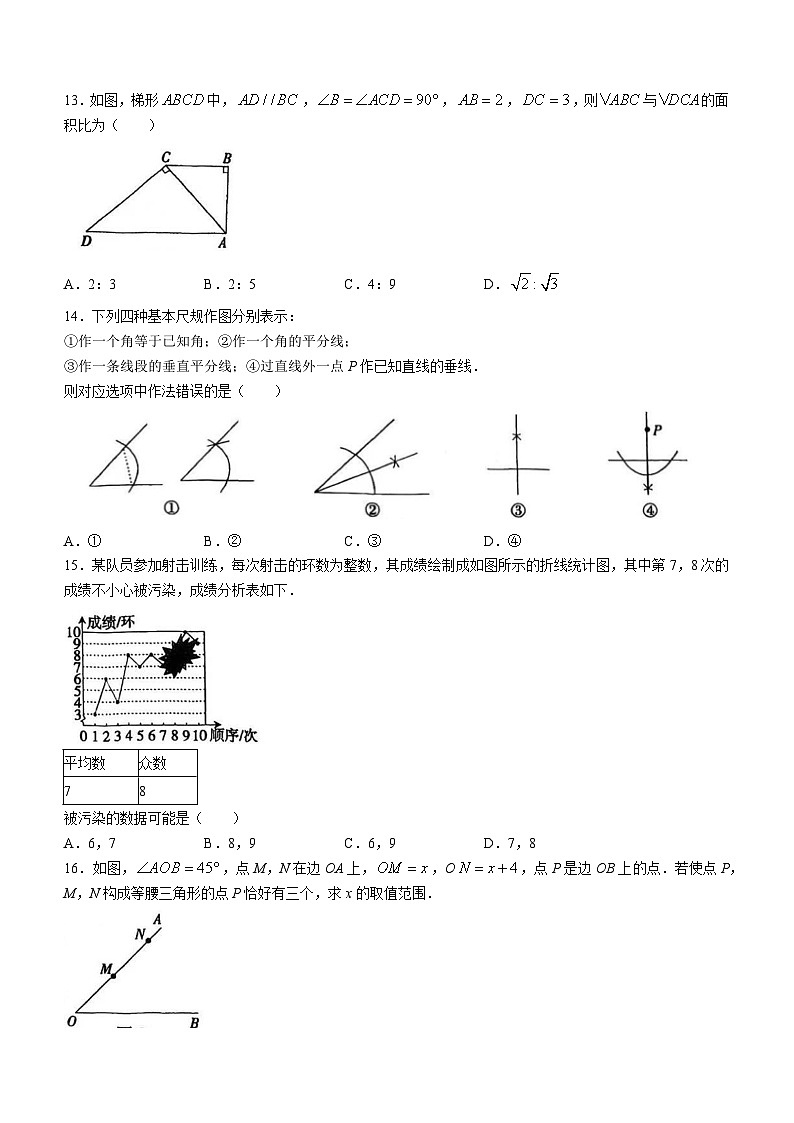
13．如图，梯形中，，，，，则与的面积比为（    ）

A．2：3 B．2：5 C．4：9 D．

14．下列四种基本尺规作图分别表示：

①作一个角等于已知角；②作一个角的平分线；

③作一条线段的垂直平分线；④过直线外一点P作已知直线的垂线．

则对应选项中作法错误的是（    ）

A．① B．② C．③ D．④

15．某队员参加射击训练，每次射击的环数为整数，其成绩绘制成如图所示的折线统计图，其中第7，8次的成绩不小心被污染，成绩分析表如下．

被污染的数据可能是（    ）

A．6，7 B．8，9 C．6，9 D．7，8

16．如图，，点M，N在边OA上，，O，点P是边OB上的点．若使点P，M，N构成等腰三角形的点P恰好有三个，求x的取值范围．

甲同学的答案是；乙同学的答案是；丙同学的答案是．则以下说法正确的是（    ）

A．只有甲正确  B．只有乙正确

C．只有甲和乙正确  D．甲、乙、丙都正确

二、填空题（本大题共3个小题，每小题3分，共9分．其中19小题第一空2分，第二空1分）

17．《“一带一路”贸易合作大数据报告（2017）》以“一带一路”贸易合作现状分析和趋势预测为核心，采集调用了8000多个种类，总计1.2亿条全球进出口贸易基础数据．1.2亿用科学记数法表示为______．

18．如图的一座拱桥，当水面宽AB为12m时，桥洞顶部离水面4m，已知桥洞的拱形是抛物线，以水平方向为x轴，建立平面直角坐标系，若选取点A为坐标原点时的抛物线解析式是，则选取点B为坐标原点时的抛物线解析式是______．

19．有三个大小相同的正六边形，可按下列方式进行拼接：

方式1：如图11－1；方式2：如图11－2；

若有四个边长均为1的正六边形，采用方式1拼接，所得图案的外轮廓的周长是______．有n个边长均为1的正六边形，采用上述两种方式的一种或两种方式混合拼接，若得图案的外轮廓的周长为18，则n的最大值为______．

三、解答题（本大题有7个小题，共69分．解答应写出文字说明、证明过程或演算步骤）

20．（本小题满分9分）

已知有理数a，b，c在数轴上对应位置如图所示：

（1）用“<”或“>”填空：______0，______0，______0，______0；

（2）化简：．

21．（本小题满分9分）

某校组织学生外出研学，旅行社报价每人收费300元，当研学人数超过50人时，旅行社给出两种优惠方案：

方案一：研学团队先交1500元后，每人收费240元；

方案二：5人免费，其余每人收费打九折（九折即原价的90%）．

（1）用代数式表示，当参加研学的总人数是人时，

用方案一共收费______元；

用方案二共收费______元；

（2）当参加研学的总人数是80人时，采用哪种方案省钱？说说你的理由．

22．（本小题满分9分）

为大力弘扬“奉献、友爱、互助、进步”的志愿服务精神，传播“奉献他人、提升自我”的志愿服务理念，某中学利用周末时间开展了“助老助残、社区服务、生态环保、网络文明”四个志愿服务活动（每人只参加一个活动），九年级某班全体同学都参加了志愿服务，班长为了解志愿服务的情况，收集整理数据后，绘制以下不完整的统计图（图13），请你根据统计图中所提供的信息解答下列问题．

（1）求该班的人数；

（2）请把折线统计图补充完整；

（3）求扇形统计图中，网络文明部分对应的圆心角的度数；

（4）小明和小丽参加了志愿服务活动，请用画树状图法或列表法求出他们参加同一服务活动的概率．

23．（本小题满分10分）

如图14，在中，过点A分别作于点E，于点F．

（1）求证：；

（2）已知，，，求CF的长．

24．（本小题满分10分）

如图，平行于轴的直尺（一部分）与反比例函数的图象交于点A，C，与轴交于点B，D，连接AC．点A，B的刻度分别为5，2，直尺的宽度BD为2，，设直线AC的解析式为．

（1）请结合图象直接写出不等式的解集；

（2）求直线AC的解析式；

（3）平行于y轴的直线与AC交于点，与反比例函数图象交于点，当这条直线左右平移时，线段EF的长为，求的值．

25．（本小题满分10分）

某农作物的生长率与温度有如下关系：如图，当时可近似用函数刻画；当时可近似用函数刻画．

（1）求h的值

（2）按照经验，该作物提前上市的天数m（天）与生长率p之间满足已学过的函数关系，部分数据如下：

求：①m关于p的函数表达式；

②用含t的代数式表示m．

③天气寒冷，大棚加温可改变农作物生长速度．大棚恒温20℃时每天的成本为100元，计划该作物30天后上市，现根据市场调查：每提前一天上市售出（一次售完），销售额可增加600元．因此决定给大棚继续加温，但加温导致成本增加，估测加温到时的成本为200元/天，但若欲加温到，由于要采用特殊方法，成本增加到400元/天．问加温到多少度时增加的利润最大？并说明理由．（注：农作物上市售出后大棚暂停使用）

26．（本小题满分12分）

木匠黄师傅用长，宽的矩形木板做一个尽可能大的圆形桌面，他设计了三种方案：

方案一：直接锯一个半径最大的圆（如图17－1）；

方案二：沿对角线AC将矩形锯成两个三角形，适当平移三角形并锯一个最大的圆（如图17－2）；

方案三：锯一块小矩形拼到矩形下面，利用拼成的木板锯一个尽可能大的圆（如图17－3）．

（1）通过计算说明方案一和方案二中，哪个圆的半径较大？

（2）在方案三中，设，圆的半径为y．

①求y关于x的函数解析式；

②当x取何值时圆的半径最大，最大半径为多少？并说明三种方案中哪一个圆形桌面的半径最大．

2023年九年级中考模拟练习内测试题

数学试卷参考答案

本答案仅供参考，若考生答案与本答案不一致，只要正确，同样得分．

一、选择题

1．A  2．C  3．A  4．C  5．C  6．D  7．B  8．C  9．B  10．B  11．B

12．A  13．C  14．C  15．D  1 6．D

二、填空题

17．

18．

【解析】由抛物线形状不变，顶点横坐标相反，纵坐标不变，可直接写出取点B为坐标原点时的抛物线解析式是．

故答案为：．

19．18  7

【解析】有四个边长均为1的正六边形，采用方式1拼接，所得图案的外轮廓的周长为；

按下图拼接，图案的外轮廓的周长为18，此时正六边形的个数最多，即n的最大值为7．

故答案为：18，7．

三、解答题

20．解：（1）由图可知：，且，

∴，，，；

故答案为：<；<；>；>；

（2）原式．

21．解：（1）方案一的收费为元，

方案二收费为元，

故答案为：；；

（2）把代入元，

把代入元，

∵，∴采用方案二省钱．

22．解：（1）该班全部人数：人；

（2），补充折线统计如图所示：

（3）；

（4）分别用“1，2，3，4”代表“助老助残、社区服务、生态环保、网络文明”四个服务活动，列表如下：

则所有等可能的情况有16种，其中他们参加同一服务活动的情况有4种，

所以他们参加同一服务活动的概率．

23．（1）证明：∵四边形为平行四边形，∴，

∵于点，于点，

∴，，

∴，，∴；

（2）解：在中，∵，，

∴，∴

∴根据勾股定理，得．

∵在Rt和Rt中，，，

∴，∴，

∴，∴．

24．解：（1）根据图象可知：不等式的解集为；

（2）将点坐标代入中，得，

∴反比例函数解析式为；

又∵，∴点的坐标，

将和的坐标分别代入，

得解得，

∴直线AC的解析式为；

（3）当时，点的纵坐标为，点的纵坐标为，

依题意，得，解得或．

25．解：（1）把代入得：

解得或，

∵，∴．

（2）①由表格可知，是的一次函数，设，

把（0.2，0），（0.3，10）代入得

解得∴．

②当时，提前20天上市，增加的利润最大，理由如下：当时，

∴；

当时，

∴

∴

③当时，增加的利润为：

∴．当时，增加的利润的最大值为；

当，增加的利润为：

∴当时，增加的利润的最大值为11000元．

综上，当时，提前20天上市，增加的利润最大，最大值为11000元．

26．解：（1）方案一中的最大半径为1．

因为矩形的长宽分别为3，2，那么直接锯圆的直径最大为2，则半径最大为1；

方案二：如图，作于点，于点，设半径为，

在和中，

∴，∴，

∴，解得．

比较知，方案二中圆的半径较大；

（2）①，

∴新拼图形水平方向跨度为，竖直方向跨度为．

类似（1），所截出圆的直径最大为或较小的．

a．当时，即当时，；

b．当时，即当时，；

c．当时，即当时，．

②当时，；

当时，；

当时，，

∴方案三中，当时，最大为．

，∴方案三中圆形桌面的半径最大．