

2023年重庆市渝中区巴蜀中学校中考三模数学试题(含答案)
展开数学
一、选择题(每题4分,共40分)
1.4的相反数是( )
A.-4 B.4 C. D.
2.下列图形是中心对称图形的是( )
A. B. C. D.
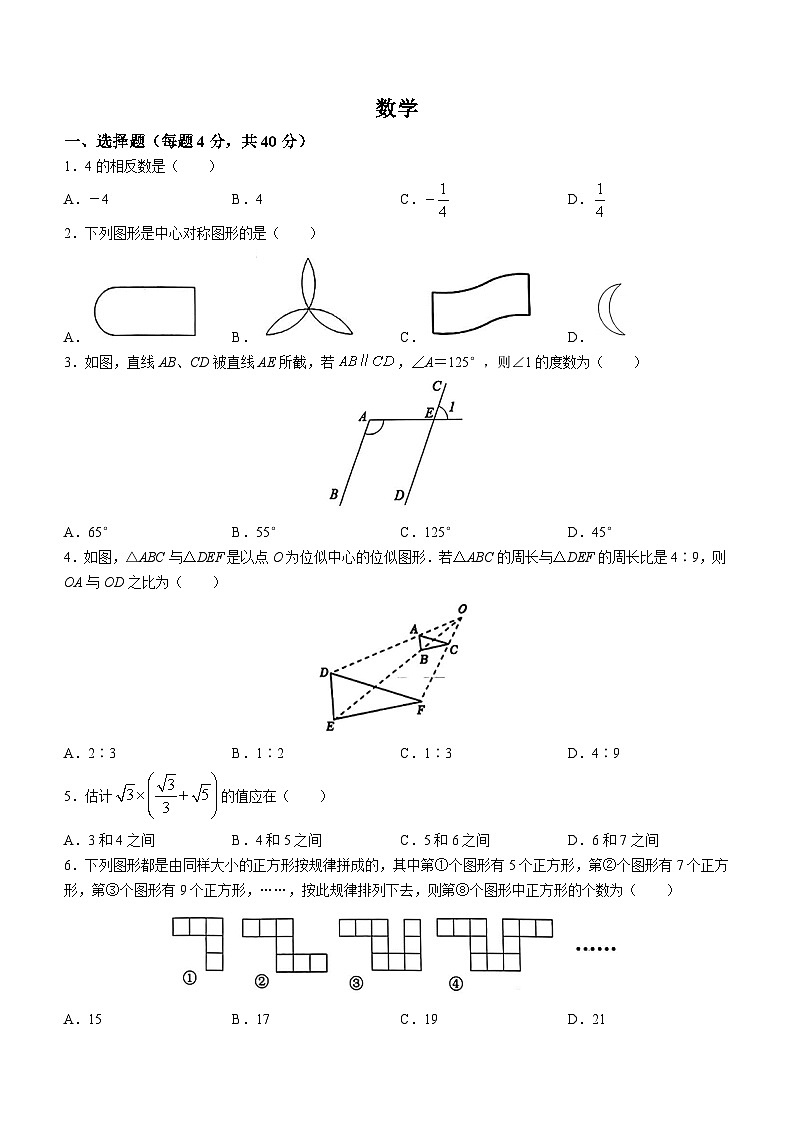
3.如图,直线AB、CD被直线AE所截,若,∠A=125°,则∠1的度数为( )
A.65° B.55° C.125° D.45°
4.如图,△ABC与△DEF是以点O为位似中心的位似图形.若△ABC的周长与△DEF的周长比是4∶9,则OA与OD之比为( )
A.2∶3 B.1∶2 C.1∶3 D.4∶9
5.估计的值应在( )
A.3和4之间 B.4和5之间 C.5和6之间 D.6和7之间
6.下列图形都是由同样大小的正方形按规律拼成的,其中第①个图形有5个正方形,第②个图形有7个正方形,第③个图形有9个正方形,……,按此规律排列下去,则第⑧个图形中正方形的个数为( )
A.15 B.17 C.19 D.21
7.反比例函数的图象过点,下列各点在反比例函数的图象上的是( )
A. B. C. D.
8.如图,是的直径,延长至切于点,过点作交于点,连接.若,则.的长为( )
A.3 B. C.6 D.
9.如图,矩形中,点为边的中点,连接,过作交于点,连接,若,则的度数为( )
A. B. C. D.
10.对于整式:、、、,在每个式子前添加“+”或“-”号,先求和再求和的绝对值,称这种操作为“全绝对”操作,并将绝对值化简的结果记为.例如:,当时,;当时,,所以或.
下列相关说法正确的个数是:( )
①至少存在一种“全绝对”操作使得操作后化简的结果为常数;
②若一种“全绝对”操作的化简结果为M=-2x+k(k为常数),则x≤2;
③所有可能的“全绝对”操作后的式子化简后有16种不同的结果,
A.0 B.1 C.2 D.3
二、填空题(每题4分,共32分)
11.计算:______.
12.一个正多边形的内角为135°,则这个正多边形的边数为______.
13.一个不透明的口袋中有2个红球和1个白球,它们除了颜色其他完全相同.从中随机取出一个小球,记下颜色后放回,摇匀后再从中随机取出一个小球,记下颜色,则两次取出的小球颜色相同的概率为______.
14.某商品一月份的销售额为2500元,三月份的销售额为1600元,设该商品二、三月份销售额平均减少率为x,则根据题意,可列方程为______.
15.如图,在△ABC中,AB=AC,AB的垂直平分线交AC于点D,交AB于点E,连接BD,若AB=5,BC=3,则△BDC的周长为______.
16.如图,在Rt△ABC中,∠ACB=90°,AC=4,∠B=30°,以AC为直径的半圆交AB于点D,则图中阴影部分的面积是______.
17.若关于的不等式组的解集为,且关于的分式方程有非负整数解,则所有满足条件的整数的值的和是______.
18.对于四位数,若千位上的数字与百位上的数字的差的两倍等于十位上的数字与个位上的数字的差,则把叫做“双倍差数”,将“双倍差数”的个位数字去掉得到的数记为,将千位数字去掉得到的数记为,并规定,则______;若一个四位数(0≤a≤8,0≤b≤7,0≤c≤3,0≤d≤8,a,b,c,d均为整数)是“双倍差数”,且F(M)除以13余1,则满足条件的M的最大值为______.
三、解答题(共78分)
19.(8分)由平行四边形如何构造菱形?如图,平行四边形ABCD中,BE平分∠ABC,珈跏的思路是:过点A作BE的垂线AG,垂足为G,交线段BC于点F,然后利用四边相等的四边形是菱形即可完成构造,请根据以上思路完成作图和填空.
证明:用直尺和圆规过点A作BE的垂线AG交BE于点G,交BC于点F,连接EF(只保留作图痕迹)
∵四边形ABCD是平行四边形,∴①______
∴∠AEB=∠CBE,∵BE平分∠ABC,
∴∠ABE=∠CBE,∴②______
∴AB=AE,∵AF⊥BE,∴∠AGB=∠FGB=90°
又∵BG=BG,∴△ABG≌△FBG(ASA),
∴③______,∵AB=AE,AF⊥BE,
∴AF垂直平分BE,∴④∴______,
BF=BA=EF=AE,∴四边形ABFE是菱形.
20.(10分)计算
(1)
(2)
21.(10分)为了迎接中考体考,在临考前初三年级进行了全真模拟考试,并对各个项目进行了统计和分析.某数学兴趣小组从初三年级男、女同学中各随机抽取20名学生,对其一分钟跳绳的个数进行整理和分析(跳绳个数记为x,共分为五组:A.100≤x<180,B.180≤x<190,C.190≤x<200,D.200≤x<210,E.x≥210).下面给出了部分信息:
被抽取的男同学的跳绳个数在C组的数据是:192 195 195 195 195 194
被抽取的女同学的跳绳个数在C组的数据是:193 196 193 192 196 196 196 196
被抽取的男、女同学跳绳个数的平均数、中位数、众数如下表:
| 平均数 | 中位数 | 众数 |
男同学 | 196 | a | 195 |
女同学 | 196 | 196 | b |
(1)填空:a=______,b=______,m=______;
(2)根据以上数据分析,你认为该校初三______(男、女)同学一分钟跳绳更优秀,请说明理由(写出一条理由即可);
(3)若该校初三年级参加此次体育模拟考试的男生有800人,女生有1000人,请你估计全年级跳绳个数不少于200个的人数.
22.(10分)喜迎熊猫丫丫回国,重庆一玩具加工厂计划甲车间加工熊猫玩偶600个,工作5天后,增加了工人人数,每天比增加前多加工20个,又加工了两天完成了任务.
(1)求甲车间增加工人人数后每天加工熊猫玩偶的个数;
(2)由于该玩偶深受消费者喜欢,工厂决定扩大生产,安排乙车间加工生产该熊猫玩偶1000个.该车间在加工完成一半后,改进了加工技术,每天比改进技术前多加工,结果提前2天完成任务,求乙车间改进技术前每天加工玩偶的个数.
23.(10分)如图,四边形ABCD中,,∠B=90°,AB=3,BC=2AD=4.点P从C出发,沿着折线CB→BA运动,到达点A停止运动.设点P运动的路程为x,连接DP,记△DPC的面积为y,请解答下列问题:
(1)直接写出y关于x的函数关系式,并写出自变量x的取值范围;
(2)在平面直角坐标系中,画出该函数的图象,并写出该函数的一条性质;
(3)结合图象,当△DPC的面积大于四边形ABCD面积的时,直接写出x的取值范围.(结果保留一位小数,误差不超过0.2)
24.(10分)如图为某体育公园部分示意图,C为公园大门,A、B、D分别为公园广场、健身器材区域、儿童乐园.经测量:A、B、C在同一直线上,且A、B在C的正北方向,AB=240米,点D在点B的南偏东75°方向,在点A的东南方向.
(1)求B、D两地的距离;(结果精确到0.1m)
(2)大门C在儿童乐园D的南偏西60°方向,由于安全需要,现准备从儿童乐园D牵一条笔直的数据线到大门C的控制室,请通过计算说明公园管理部门采购的380米数据线是否够用(接头忽略不计).(参考数据:)
25.(10分)如图,在平面直角坐标系中,拋物线与轴交于两点,与y轴交于点C.
(1)求△ABC的面积;
(2)点P是直线BC下方抛物线上一动点,过P作PQ⊥BC于点2,求线段PQ的最大值及此时点P的坐标;
(3)将抛物线沿射线平移个单位得到新抛物线,新抛物线与原抛物线交于点,将沿直线平移得到(不与重合),若以点,,为顶点的三角形是以为腰的等腰三角形,请直接写出所有符合条件的点的坐标,并写出求解点坐标的其中一种情况的过程.
26.(10分)如图,在等边△ABC中,D为△ABC内一点,连接AD、BD、CD,∠ADB=90°,E为BD上一点,连接AE.
(1)如图1,若AE平分∠BAD,AD=2,BC=3,求BE的长;
(2)如图2,若∠BAE=∠ACD,且E为BD的中点,求证:;
(3)如图3,若AB=4,将△ADC沿AC翻折得到,F为BC上一点,BF=3CF,连接,当最小时,过作的垂线,P是垂线上一动点,连接AP,将线段PA绕点P逆时针旋转60°得到线段PQ,连接,请直接写出的最小值.
参考答案
一、选择题(每题4分,共40分)
ACBDB CADBC
二、填空题(每题4分,共32分)
11. 12.8 13. 14.
15.8 16. 17. 18.82,6939
三、解答题(共78分)
19.如下图所示:
①,②∠AEB=∠ABE,③BF=BA,④BF=EF
20.(1)解:原式
(2)解:原式
21.解:(1)a=193,b=196,m=20;
(2)女同学跳绳成绩较好;理由如下:
女同学跳绳次数的中位数196高于男同学跳绳次数的中位数193,∴女同学成绩较好.
(3)(人)
答:跳绳个数不少于200个的人数大约为500人.
22.(1)解:设甲车间增加工人后每天加工x个,则原计划每天加工(x-20)个.
根据题意,得:5(x-20)+2x=600,解得:x=100
答:甲车间增加工作人员后每天加工100个.
(2)解:设乙车间原来每天加工y个,先加工生产了1000÷2=500个
根据题意,得:,解得:
经检验,y=50是原分式方程的解且符合实际意义.
答:乙车间原来每天加工50个.
23.解:(1)
(2)图象如图所示,性质如下:
【增减性】:当0<x<4时,y随x的增大而增大;当4<x<7时,y随x的增大而减小.
【最值】:该函数在自变量的取值范围内,有最大值,无最小值;
当x=4时,函数取得最大值6.
(3)2.7≤x<6.
24.解:(1)过点B作BP⊥AD于点P,
由题可知∠BAD=45°,∠CBD=75°,
∴∠ADB=30°,∴AB=240,
∴,∴
答:B、D两地的距离为339.4m.
(2)过点B作BM⊥DC于点M,
由(1)可得,∠CDB=45°,∠CBD=75°,
∴∠DCB=60°,∴,
∴∠CBM=30°,∴,
∴,∵380>378.56,
答:公园管理部门采购的380米数据线够用.
25.解:(1)∵抛物线与轴交于两点,与轴交于点,
∴当时,,,∴
当时,
∴,,∴,
∴,∴.
(2)∵
∴直线的表达式为:
过点作轴交直线于点,
设,
则,∴
∵轴
易得,∴
∴
∴当时,,此时
(3),
过程如下:原抛物线,
沿射线平移个单位得到新抛物线,
由,得,
∵在直线上平移,∴在直线上运动
∴设,∴
∴当,即
解得(舍),,∴.
26.解:(1)过点作,可证:,
∴,又∵,∴.
在中,,
设,则,
在中,,
∴,解得,∴.
(2)在AE上截取AQ=CD,连接BQ.延长AE至P点,使EP=AE,连接BP.
先证:△CAD≌△ABQ,∴∠ABQ=∠CAD,BQ=AD.
再证:△BPE≌△DAE,∴BP=AD=BQ.
∴∠P=∠BQP=∠QAD,
又∵∠BQP=∠QBA+∠BAQ=∠CAD+∠BAQ,
∴,∴.
(3)可知:点轨迹是以为直径画圆,经过中点,且以中点为端点的弧,将沿翻折到,则点轨迹是以为直径画圆,经过、中点,且以中点为端点的弧,连接,交于点,此时最小.分别取和,相应可得和,则点的轨迹为直线,过点作直线的垂线,垂足为,此时的值最小,等于.
可求:,∴的最小值.
2024年重庆市渝中区巴蜀中学校初三保送生考试数学试卷: 这是一份2024年重庆市渝中区巴蜀中学校初三保送生考试数学试卷,共6页。
重庆市渝中区巴蜀中学校2023-2024学年八年级上学期期末数学试题: 这是一份重庆市渝中区巴蜀中学校2023-2024学年八年级上学期期末数学试题,共13页。试卷主要包含了解答题等内容,欢迎下载使用。
重庆市渝中区巴蜀中学校2023-2024学年七年级上学期期末数学试题: 这是一份重庆市渝中区巴蜀中学校2023-2024学年七年级上学期期末数学试题,共9页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












