






2024年高考数学一轮复习(新高考版) 第8章 §8.12 圆锥曲线中定点与定值问题课件PPT
展开例1 (2022·全国乙卷)已知椭圆E的中心为坐标原点,对称轴为x轴、y轴,且过A(0,-2), 两点.(1)求E的方程;
设椭圆E的方程为mx2+ny2=1(m>0,n>0且m≠n),
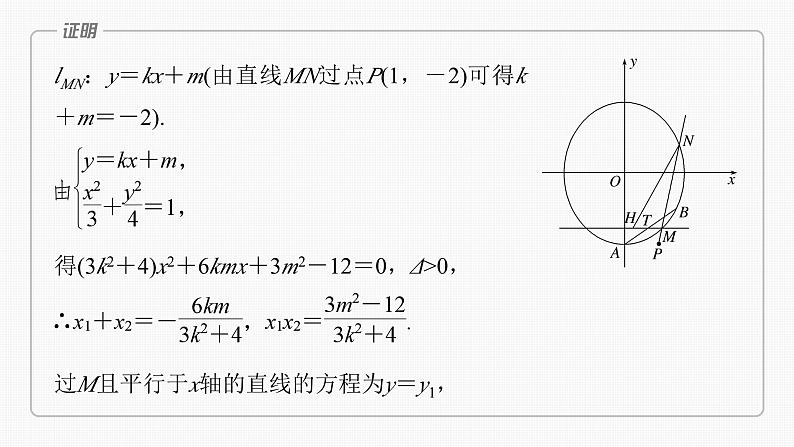
(2)设过点P(1,-2)的直线交E于M,N两点,过M且平行于x轴的直线与线段AB交于点T,点H满足 .证明:直线HN过定点.
当直线MN的斜率不存在时,lMN:x=1,
此时直线HN过定点(0,-2).当直线MN的斜率存在时,如图,设M(x1,y1),N(x2,y2),
lMN:y=kx+m(由直线MN过点P(1,-2)可得k+m=-2).
得(3k2+4)x2+6kmx+3m2-12=0,Δ>0,
过M且平行于x轴的直线的方程为y=y1,
y1+y2=(kx1+m)+(kx2+m)
x1y2+x2y1=x1(kx2+m)+x2(kx1+m)
∴直线HN过定点(0,-2).综上,直线HN过定点(0,-2).
求解直线或曲线过定点问题的基本思路(1)把直线或曲线方程中的变量x,y当作常数看待,把方程一端化为零,既然是过定点,那么这个方程就要对任意参数都成立,这时参数的系数就要全部等于零,这样就得到一个关于x,y的方程组,这个方程组的解所确定的点就是直线或曲线所过的定点.(2)由直线方程确定其过定点时,若得到了直线方程的点斜式y-y0=k(x-x0),则直线必过定点(x0,y0);若得到了直线方程的斜截式y=kx+m,则直线必过定点(0,m).
跟踪训练1 (2023·郑州质检)已知椭圆C: =1(a>b>0)的上顶点和两焦点构成的三角形为等腰直角三角形,且面积为2,点M为椭圆C的右顶点.(1)求椭圆C的方程;
又a2-b2=c2,则a=2,
(2)若经过点P(t,0)的直线l与椭圆C交于A,B两点,实数t取何值时以AB为直径的圆恒过点M ?
由(1)知M(2,0),若直线l的斜率不存在,则直线l的方程为x=t(-2
得(1+2k2)x2-4k2tx+2k2t2-4=0.
易得(1+k2)x1x2-(2+k2t)(x1+x2)+4+k2t2=0,即(1+k2)(2k2t2-4)-(2+k2t)·4k2t+(4+k2t2)(1+2k2)=0,
整理得k2(3t2-8t+4)=0,因为k不恒为0,
例2 (2022·蚌埠模拟)已知双曲线C: =1(a>0,b>0)的虚轴长为4,直线2x-y=0为双曲线C的一条渐近线.(1)求双曲线C的标准方程;
∵虚轴长为4,∴2b=4,即b=2,∵直线2x-y=0为双曲线C的一条渐近线,
(2)记双曲线C的左、右顶点分别为A,B,过点T(2,0)的直线l交双曲线C于点M,N(点M在第一象限),记直线MA的斜率为k1,直线NB的斜率为k2,求证: 为定值.
由题意知,A(-1,0),B(1,0),由题可知,直线l的斜率不能为零,故可设直线l的方程为x=ny+2,设M(x1,y1),N(x2,y2),
圆锥曲线中的定值问题的常见类型及解题策略(1)求代数式为定值.依题设条件,得出与代数式参数有关的等式,代入代数式,化简即可得出定值.(2)求点到直线的距离为定值.利用点到直线的距离公式得出距离的解析式,再利用题设条件化简、变形求得.(3)求某线段长度为定值.利用长度公式求得解析式,再依据条件对解析式进行化简、变形即可求得.
跟踪训练2 (2022·郑州模拟)已知点F(0,1),直线l:y=4,P为曲线C上的任意一点,且|PF|是P到l的距离的 .(1)求曲线C的方程;
(2)若经过点F且斜率为k(k≠0)的直线交曲线C于M,N两点,线段MN的垂直平分线交y轴于点H,求证: 为定值.
设线段MN的中点为T(x0,y0),
1.已知抛物线C:x2=2py(p>0)与圆O:x2+y2=12相交于A,B两点,且点A的横坐标为 .F是抛物线C的焦点,过焦点的直线l与抛物线C相交于不同的两点M,N.(1)求抛物线C的方程;
代入解得p=2,所以抛物线的方程为x2=4y.
(2)过点M,N作抛物线C的切线l1,l2,P(x0,y0)是l1,l2的交点,求证:点P在定直线上.
设直线MN的方程为y=kx+1,代入x2=4y,得x2-4kx-4=0,所以x1x2=-4,所以点P在y=-1上,结论得证.
(2)设Q(1,0),直线x=t(t∈R)不经过P点且与C相交于A,B两点,若直线BQ与C交于另一点D,证明:直线AD过定点M.
显然直线BQ的斜率不为零,设直线BQ:x=my+1,B(x1,y1),D(x2,y2),A(x1,-y1),
依题意得m2-3≠0,且Δ=4m2+8(m2-3)>0,即m2>2且m2≠3,
所以直线AD过定点M(3,0).
(1)求C的方程,并说明C是什么曲线;
所以曲线C是中心在原点,焦点在x轴上的椭圆(不含左右顶点).
(2)过点D(2,0)的直线l交C于P,Q两点,过点P作直线x=3的垂线,垂足为G,过点O作OM⊥QG,垂足为M.证明:存在定点N,使得|MN|为定值.
由(1)知直线l与x轴不重合,可设l:x=my+2,P(x1,y1),Q(x2,y2),
Δ=24m2+24>0,
因为G(3,y1),Q(my2+2,y2),
则直线QG的方程为y-y1=2y1(x-3),
因为OM⊥QG,所以△OHM为直角三角形,
4.(2022·杭州质检)如图,已知椭圆C1: =1,椭圆C2: =1,A(-2,0),B(2,0),P为椭圆C2上的动点且在第一象限,直线PA,PB分别交椭圆C1于E,F两点,连接EF交x轴于Q点,过B点作BH交椭圆C1,C2于G,H点,且BH∥PA.(1)证明:kBF·kBG为定值;
(2)证明:直线GF过定点,并求出该定点;
当直线GF的斜率存在时,设GF的方程为y=k(x-t)(k≠0),
则Δ=64k4t2-16(4k2+3)(k2t2-3)=48(4k2+3-k2t2)>0,
约去k2并化简得t2-3t+2=0,解得t=1(t=2不符合题意,舍去),此时直线GF过定点(1,0);当直线GF的斜率不存在时,设GF的方程为x=m,其中m≠2,
综上,直线GF过定点(1,0).
(3)若记P,Q两点的横坐标分别为xP,xQ,证明:xPxQ为定值.
设PA的方程为y=k1(x+2)(k1>0),
2024年新高考数学第一轮复习课件:第44讲 第3课时 圆锥曲线中的定值与定点问题: 这是一份2024年新高考数学第一轮复习课件:第44讲 第3课时 圆锥曲线中的定值与定点问题,共11页。
新高考数学一轮复习课件 第8章 §8.11 圆锥曲线中定点与定值问题: 这是一份新高考数学一轮复习课件 第8章 §8.11 圆锥曲线中定点与定值问题,共60页。PPT课件主要包含了高考数学一轮复习策略,第八章,课时精练等内容,欢迎下载使用。
高中数学高考第8讲 第2课时 圆锥曲线中的定值、定点与存在性问题课件PPT: 这是一份高中数学高考第8讲 第2课时 圆锥曲线中的定值、定点与存在性问题课件PPT,共34页。PPT课件主要包含了word部分,点击进入链接等内容,欢迎下载使用。












