吉林省松原市乾安县2023届九年级学业水平模拟考试数学试卷(含答案)

    乾安县2023年初中毕业生学业水平模拟考试

数   学   试   题

数学试题共8页，包括六道大题，共26道小题。全卷满分120分。考试时间为120分钟。注意事项：1.答题前，考生务必将自己的姓名、准考证号填写在答题卡上，并将条形码准确粘贴在条形码区域内。2.答题时，考生务必按照考试要求在答题卡上的指定区域内作答，在草稿

纸、试题上答题无效。

一、选择题（本大题共6小题，每小题2分，共12分）

1. 直六棱柱如图所示，它的俯视图是（　　）

   A．     B．      C．          D．

2. 下列计算正确的是（    ）

A．    B．    C．      D．

3.一条古称在称物时的状态如图所示，已知，则（    ）

A.               B.                 C.                  D.

4.如图是小明同学在体育课上跳远后留下的脚印，他的跳远成绩是线段（    ） 的长度，这样测量的依据是（   ）

A. AM,两点之间，线段最短 B.AM, 两点确定一条直线

C. BN,垂线段最短 D.BN,三角形两边之和大于第三边

5.若关于x的一元二次方程有两个不相等的实数根，则整数k的最小值是（     ）

A． B． C．0 D．1

6.工人师傅为检测该厂生产的一种铁球的大小是否符合要求，设计了一个如图（1）所示的工件槽，其两个底角均为90°，将形状规则的铁球放入槽内时，若同时具有图（1）所示的A、B、E三个接触点，该球的大小就符合要求．图（2）是过球心及A、B、E三点的截面示意图，已知⊙O的直径就是铁球的直径，AB是⊙O的弦，CD切⊙O于点E，AC⊥CD、BD⊥CD，若CD=16cm，AC=BD=4cm，则这种铁球的直径为（    ）

A 10cm B. 15cm C. 20cm D. 24cm 

二、填空题（本大题共8小题，每小题3分，共24分）

7.负数的概念最早出现在中国古代著名的数学专著《九章算术》中，负数与对应的正数“数量相等，意义相反”，如果向东走了5米，记作＋5米，那么向西走5米，可记作______米．

8. 2023年全国两会在北京圆满落下帷幕．《两会微博热度报告》显示，网会相关话题信息阅读量达78200000000．数据78200000000用科学记数法表示为_________.

9.计算的值等于________.

10.分解因式：______．

11.大自然是美的设计师，即使是一片小小的树叶，也蕴含着“美学”.如图,,这个比值介于整数n和n+1之间,则n的值是______________.     

12.反比例函数的图像经过、两点，当时，，写出符合条件的的值_________（答案不唯一，写出一个即可）.

13.如图，为了测量山坡的护坡石坝高，把一根长为4.5m的竹竿AC斜靠在石坝旁，量出竿上AD长为1m时，它离地面的高度DE为0.6m，则坝高CF为 　 　m． 

14.如图，在中，，将绕点A逆时针旋转，得到，连接并延长交AB于点D，当时，的长是_________.

三、解答题 (每小题5分,共20分)

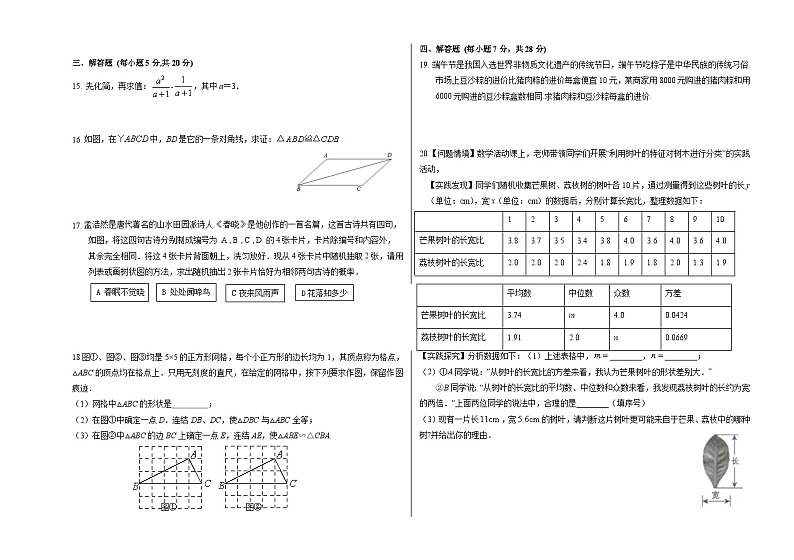
15. 先化简，再求值：﹣，其中a＝3．

16. 如图，在中，BD是它的一条对角线，求证：.

17. 孟浩然是唐代著名的山水田园派诗人.《春晓》是他创作的一首名篇，这首古诗共有四句，

如图，将这四句古诗分别制成编号为 A , B , C , D 的4张卡片，卡片除编号和内容外，

其余完全相同．将这4张卡片背面朝上，洗匀放好．现从4张卡片中随机抽取2张，请用

列表或画树状图的方法，求出随机抽出2张卡片恰好为相邻两句古诗的概率．

18.图①、图②、图③均是5×5的正方形网格，每个小正方形的边长均为1，其顶点称为格点，△ABC的顶点均在格点上．只用无刻度的直尺，在给定的网格中，按下列要求作图，保留作图痕迹．

（1）网格中△ABC的形状是         ；

（2）在图①中确定一点D．连结DB、DC，使△DBC与△ABC全等；

（3）在图②中△ABC的边BC上确定一点E，连结AE，使△ABE∽△CBA.

图①                 图②

四、解答题 (每小题7分，共28分)

19. 端午节是我国入选世界非物质文化遗产的传统节日，端午节吃粽子是中华民族的传统习俗.市场上豆沙粽的进价比猪肉粽的进价每盒便宜10元，某商家用8000元购进的猪肉粽和用6000元购进的豆沙粽盒数相同.求猪肉粽和豆沙粽每盒的进价.

20.【问题情境】数学活动课上，老师带领同学们开展“利用树叶的特征对树木进行分类”的实践活动，

【实践发现】同学们随机收集芒果树、荔枝树的树叶各10片，通过测量得到这些树叶的长y（单位：cm），宽x（单位：cm）的数据后，分别计算长宽比，整理数据如下：

【实践探究】分析数据如下：（1）上述表格中，________，________；

（2）①A同学说：“从树叶的长宽比的方差来看，我认为芒果树叶的形状差别大．”

②B同学说：“从树叶的长宽比的平均数、中位数和众数来看，我发现荔枝树叶的长约为宽的两倍．”上面两位同学的说法中，合理的是________（填序号）

（3）现有一片长，宽的树叶，请判断这片树叶更可能来自于芒果、荔枝中的哪种树?并给出你的理由．

21. 一个用电器的电阻R是可调节的，其范围为110≤R≤220Ω，已知电压为220V，这个用电         器的电路图如图所示.

（1）写出功率P与电阻R的函数关系式；

（2）求这个用电器功率P的取值范围.

22.我国珠峰科考团对珠穆朗玛峰进行综合科学考察，搭建了世界最高海拔的自动气象站，还通过释放气球方式进行了高空探测．某学校兴趣小组开展实践活动，通过观测数据，计算气球升空的高度AB．如图，在平面内，点B，C，D在同一直线上，垂足为点B，，， ，求AB的高度．（精确到）（参考数据：﹐﹐，）

五、解答题 (每小题8分，共16分)

23. 某种机器工作前先将空油箱加满，然后停止加油立即开始工作，当停止工作时，油箱中油量为．在整个过程中，油箱里的油量（单位：）与时间（单位：）之间的关系如图所示．

（1）机器每分钟加油量为_____，机器工作的过程中每分钟耗油量为_____；

（2）求机器工作时关于的函数解析式，并写出自变量的取值范围；

（3）直接写出油箱中油量为油箱容积的一半时的值．

24．综合与实践课上，老师让同学们以“矩形的折叠”为主题开展数学活动.

（1）操作判断

操作一：对折矩形纸片ABCD，使AD与BC重合，得到折痕EF，把纸片展平；

操作二：在AD上选一点P，沿BP折叠，使点A落在矩形内部点M处，把纸片展平，连接PM，BM.根据以上操作，当点M在EF上时，写出图1中一个30°的角：             ；

（2）迁移探究

小华将矩形纸片换成正方形纸片，继续探究，过程如下：

将正方形纸片ABCD按照（I）中的方式操作，并延长PM交CD于点Q，连接BQ.

①如图2，当点M在EF上时，∠MBQ=    ，∠CBQ=        ；

②改变点P在AD上的位置（点P不与点A，D重合），如图3，判断∠MBQ与∠CBQ的数量关系，并说明理由.

（3）拓展应用

在（2）的探究中，已知正方形纸片ABCD的边长为8cm，当FQ=1cm时，直接写出AP的长．

六、解答题 (每小题10分，共20分)

 25．如图，在△ABC 中，∠C＝90°，AC＝BC＝4，P，Q 两点同时从 C 出发，点 P 以每秒 2 个单位长度的速度沿 CB 向终点 B 运动；点 Q 以每秒 1 个单位长度的速度沿 CA 向终点 A 运动，以 CP，CQ 为邻边作矩形 CPMQ．当点 P 停止运动时，点 Q 继续向终点 A 运动．设点 Q 的运动时间为 t 秒．

（1）在点 P 的运动过程中，CQ＝________，BP＝________（用含 t 的代数式表示）；

（2）当点 M 落在 AB 边上时，t ＝_________s；

（3）设矩形 CPMQ 与△ABC 重合部分图形的面积为 S，求 S 与 t 之间的函数关系式.

26.如图，在平面直角坐标系中，二次函数y＝x2+bx+c的图象经过点A(0，﹣4)，点B(4，0)．

（1）求此二次函数的解析式；

（2）若点P是直线AB下方抛物线上一动点，当△PAB的面积最大时，求出点P的坐标和△PAB的最大面积；

（3）当t≤x≤t+3时，此二次函数的最大值为m，最小值为n，若m﹣n＝3，直接写出t的值．

乾安县2023年初中毕业生学业模拟考试

数学试题参考答案及评分标准

（请老师在阅卷前自做一遍答案）

一、选择题（每小题2分，共12分）

1. C      2. A       3. C        4.    C       5.  D    6.   C

二、填空题（每小题3分，共24分）

7. ； 8.   7.82×1010     ；  9.    1；  10. ；  11. 0；  12.   －1（取的一切实数均可）   ；  13.   2.7    ； 14.

三、解答题（每小题5分，共20分）

15.  解：，………3分

当时，原式．…………5分               

16. 证明：四边形ABCD平行四边形，，，………3分

在△ABD和△CDB中， ,BD=BD

…………5分

17. 解：解法1：根据题意画树状图如下：

第一张        A                   B              C              D

第二张    B   C   D           A   C    D     A   B    D       A B   C………3分

由图可知，共有12种等可能的情况数，其中抽出两张恰好是相邻两句诗的情况有6种，………4分      则P（抽出两张恰好是相邻两句诗）的概率是    

                                                             …………5分

由图可知，共有12种等可能的情况数，其中抽出两张恰好是相邻两句诗的情况有6种，………4分

则P（抽出两张恰好是相邻两句诗）的概率是=………5分

18. 解：（1）直角三角形．………1分

（2）

                                                          ………3分

                                                                                                             （3）                         … 5分

四．    解答题（每小题7分，共28分）

19. 解：设猪肉粽每盒进价a元，则豆沙粽每盒进价为元.………2分

则.………4分        解得.………5分

经检验，是原分式方程的解.………6分

答：猪肉粽每盒进价为40元，豆沙粽每盒进价为30元..………7分

20. （1）3.75，2.0    ………2分

（2）②   ………4分

（3）这片树叶更可能来自于荔枝，………5分     理由是：

这片树叶更可能来自荔枝，理由如下：这片树叶长，宽 ，长宽比大约为2.0，根据平均数这片树叶可能来自荔枝树． ……7分 

21.解：（1）根据电学知识，当U=220时，有P=，………2分

即输出功率P是电阻R的反比例函数，函数解析式为P=．………4分

（2）从（1）式可以看出，电阻越大则功率越小．
把电阻的最小值R=110代入（1）式，
得到输出功率的最大值P==440，………5分

把电阻的最大值R=220代入（1）式，
得到输处功率的最小值P==220，………6分

因此用电器的输出功率在220瓦到440瓦之间．……7分

22.解：设AB=xm，在Rt△ABC中，∠ACB=52°，

∴BC=，………3分

在Rt△ABD中，∠ADB=60°，∴BD=，………5分

又∵CD=200m，BC=CD+BD，∴，………6分

解得，答：AB的高度约为984m．………7分

五．解答题（每小题8分，共16分）

 23.（1）解：（1）3，；………2分

（2）由函数图象得：当时，机器油箱加满，并开始工作；当时，机器停止工作则自变量的取值范围为，且机器工作时的函数图象经过点

设机器工作时关于的函数解析式………3分

将点代入得：解得………5分

则机器工作时关于的函数解析式；………6分

（3）5或40．………8分

24. 解：（1）∠ABP或∠PBM或∠MBC或∠BME（注：任意写出一个即可）………1分

（2）①15,15………3分

②∠MBQ=∠CBQ(注：若没写出完判断结果，但后续证明正确，不扣分）

……4分

理由如下：

∵四边形ABCD是正方形，∴AB=BC，∠A=∠C=90°,

由轴对称性质可知，BM=AB，∠BMP=∠A=90°

∠BMQ=∠C=90°BM=BC

∵BQ是公共边，∴Rt△MBQ≌Rt△CBQ………5分

∴∠MBQ=∠CBQ……6分

(3)      cm  或       cm ………8分

六．解答题（每小题10分，共20分）

25.解：（1），；………2分

（2），，，，

四边形是矩形，，当点在边上时，，

，，   ，，故答案为：；………4分

（3）当0＜t≤时，如图①，

．，．；

………6分

当＜t≤2时，如图②，

设与相交于点，设与相交于点．则，

．；

………8分

当2＜t≤4时，如图③，

设与相交于点．则．．……10分

综上所述：．

26. 解：（1）将点A（0，﹣4），点B（4，0）代入y＝x2+bx+c，

∴ ，∴ ，∴y＝x2﹣3x﹣4；………2分

（2）过点P作PQ∥y轴交AB于点Q，

设直线AB的解析式为y＝kx+b，

∴ ，

解得，∴y＝x﹣4，………4分

设P（t，t2﹣3t﹣4），则Q（t，t﹣4），∴PQ＝t﹣4﹣（t2﹣3t﹣4）＝﹣t2+4t，

∴ ，∵0＜t＜4，

∴t＝2时，………5分△PAB面积最大值为8，此时P（2，﹣6）；………6分

（3）∵y＝x2﹣3x﹣4＝ ，∴抛物线的对称轴为直线x，………7分

①当t时，

当x＝t时，y＝t2﹣3t﹣4=n，

当x＝t+3时，=m，

∴m﹣n＝6t＝3，解得t<,应舍去；………8分

②当 ，即≤t时，当x=时，y=n，若，即：0<t时，x=t+3时，=m，∴m﹣n＝t2+3t﹣43，解得t，或t，应舍去；

若，即：≤t≤0时，x=t时，y＝t2﹣3t﹣4=m，

∴m﹣n＝t2-3t﹣43，解得：t应舍去，或t；

………9分

③当t+3，即t时，当x＝t时，y＝t2﹣3t﹣4=m，当x＝t+3时，=n，∴m﹣n＝t2﹣3t﹣4﹣（t2+3t﹣4）＝﹣6t＝3，

解得t> ，应舍去；综上所述：t的值为或．………10分

此答案仅供参考，若有其它正确做法正常给分！