北师大版数学七年级下册 期末考试预测卷（无答案）

这是一份北师大版数学七年级下册 期末考试预测卷（无答案），共8页。试卷主要包含了选择题，填空题，18.作图题等内容，欢迎下载使用。
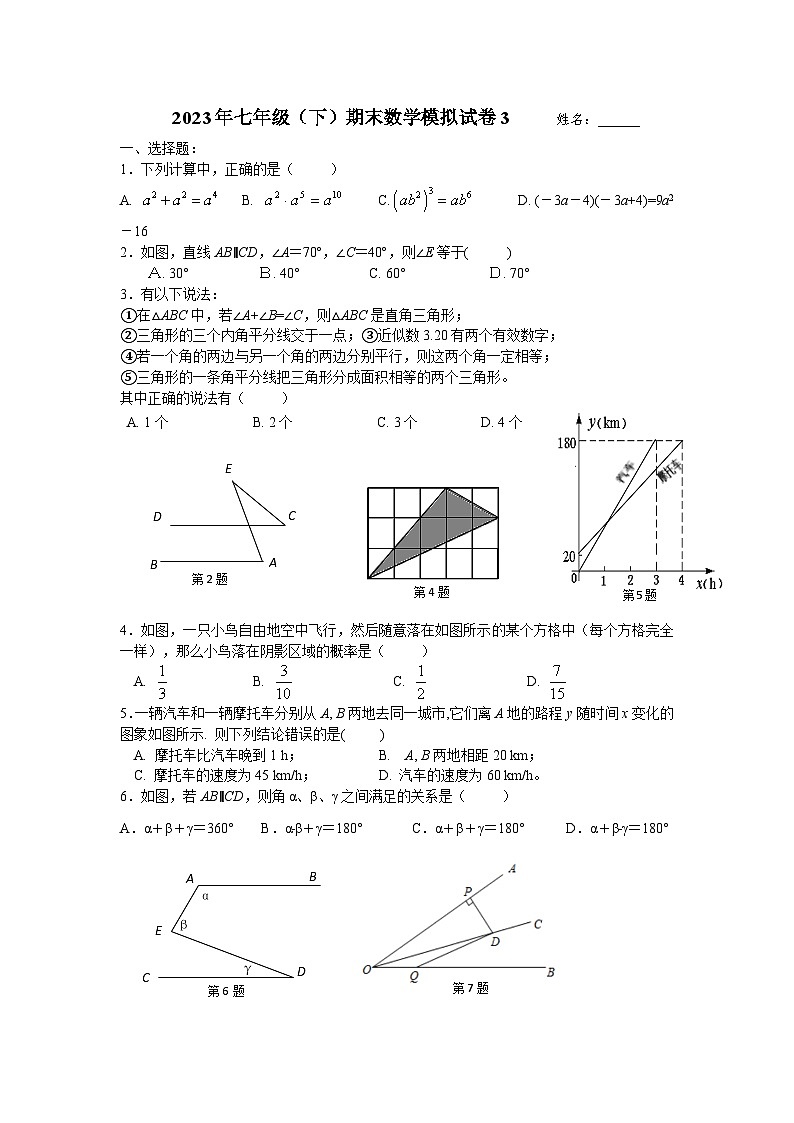
  2023年七年级（下）期末数学模拟试卷3     姓名：______一、选择题：1．下列计算中，正确的是（     ）A.    B.        C.      D. (－3a－4)(－3a+4)=9a2－162．如图，直线AB∥CD，∠A＝70，∠C＝40，则∠E等于(      )Ａ. 30°　        Ｂ. 40°　        C. 60°　          Ｄ. 70°3．有以下说法：①在△ABC中，若∠A+∠B=∠C，则△ABC是直角三角形；②三角形的三个内角平分线交于一点；③近似数3.20有两个有效数字；④若一个角的两边与另一个角的两边分别平行，则这两个角一定相等；⑤三角形的一条角平分线把三角形分成面积相等的两个三角形。其中正确的说法有（     ）A. 1个            B. 2个            C. 3个         D. 4个         4．如图，一只小鸟自由地空中飞行，然后随意落在如图所示的某个方格中（每个方格完全一样），那么小鸟落在阴影区域的概率是（     ）A.             B.             C.               D. 5．一辆汽车和一辆摩托车分别从A, B两地去同一城市,它们离A地的路程y随时间x变化的图象如图所示. 则下列结论错误的是(     )A. 摩托车比汽车晚到1 h；           B.  A, B两地相距20 km；C. 摩托车的速度为45 km/h；         D. 汽车的速度为60 km/h。6．如图，若AB∥CD，则角α、β、γ之间满足的关系是（     ）
A．α＋β＋γ＝360°　  B．α﹣β＋γ＝180°       C．α＋β＋γ＝180°　    D．α＋β﹣γ＝180°       7.如图，射线OC是∠AOB的角平分线，D是射线OC上一点，DP⊥OA于点P，DP=5，若点Q是射线OB上一点，OQ=3，则△ODQ的面积是(    )A. 6.5          B. 7.5            C. 8              D. 108. 若，那么代数式M应是（    ）A.        B.       C.       D.  二、填空题：  9. 计算：=__________10．如图是4×4正方形网格，其中已有3个小方格涂成了黑色．现在要从其余13个白色小方格中选出一个也涂成黑色，使整个涂成黑色的图形成为轴对称图形，这样的白色小方格有　   　个．11. 已知等腰三角形的两边长分别4cm和9cm ，则等腰三角形周长为          cm.。12. 长度单位1nm= m，目前发现一种新型病毒直径为25 100nm，用科学记数法表示该病毒直径是___________m;13. 如图，在△ABC中，已知D，E，F分别是BC，AD，BE上的中点，且△ABE的面积为8cm2，则△CEF的面积为__________cm2.        14. 如图，点P关于OA,OB的对称点分别为C,D，连接CD，交OA于M，交OB于N，若△PMN的周长是8厘米，则线段CD的长为          厘米。15．如图，P为∠MON内部的已知点，连接OP，A为OM上的点，B为ON上的点，当△PAB周长的最小值与OP的长度相等，∠MON的度数为　   　°．16.如图,是用火柴棍摆成的边长分别是1，2，3 根火柴棍时的正方形．当边长为n根火柴棍时，设摆出的正方形所用的火柴棍的根数为，则＝_______． （用n的代数式表示）      17.如上右图，△ABD与△ACE都是等边三角形，且AB≠AC，下列结论：①BE＝CD；  ②∠BOD＝60°；  ③∠BDO＝∠CEO；④若∠BAC＝90°，DA∥BC，则BC⊥EC． 其中正确的是 　      　（填序号）． 三、18.作图题：（用圆规、直尺作图，不写作法，但要保留作图痕迹）已知：∠β和线段a，求作△ABC，使得∠A＝∠β，∠B＝2∠β，边AB＝a．             四．解答题：19．计算：(1)          (2)   (利用乘法公式计算)                   20.化简求值：,其中       21.某商场为了吸引顾客，设立了一个可以自由转动的转盘（如图6），并规定：顾客消费100元（含100元）以上，就能获得一次转盘的机会，如果转盘停止后，指针正好对准九折、八折、七折区域，顾客就可以获得此项待遇。 某顾客正好消费120元，他转一次转盘，获得打折待遇的概率是多少？他获得九折、八折、七折的概率分别是多少？              22． 阅读材料，大数学家高斯在上学读书时曾经研究过这样一个问题：1+2+3+…+100＝？经过研究，这个问题的一般性结论是:1+2+3+…+，其中ｎ是正整数。现在我们来研究一个类似的问题：1×2+2×3+…＝？观察下面三个特殊的等式:    ;;.将这三个等式的两边相加，可以得到1×2+2×3+3×4＝.读完这段材料，请你思考后回答：⑴       　　　　　　　.⑵       　　　　　　　　　　　.⑶       的结果是多少？（写出中间过程）       23．已知：如图，AB∥CD，∠B＝∠D．点EF分别在AB、CD上．连接AC，分别交DE、BF于G、H．求证：∠1+∠2＝180°证明：∵AB∥CD，∴∠B＝　   　．（　                      　）又∵∠B＝∠D，∴　   　＝　   　．（等量代换）∴　   　∥　   　．（　                      　）∴∠1+∠2＝180°．（　                      　） 24．如图所示，A、B两地相距50千米，甲于某日下午1时骑自行车从A地出发驶往B地，乙也于同日下午骑摩托车按同路从A地出发驶往B地，如图所示，图中的折线PQR和线段MN分别表示甲、乙所行驶的路程S与该日下午时间t之间的关系．根据图象回答下列问题： （1）甲和乙哪一个出发的更早？__________; 早出发________小时； （2）甲和乙哪一个更早到达B城，__________; 早到________小时； （3）写出乙骑摩托车的速度________千米/时; 甲骑自行车在QR段的平均速度是________千米/时．（4）乙出发大约用多长时间就追上甲？此时距离B地多远？ （5）求乙出发多长时间，甲、乙相距10千米？解：（4）         （5）        25．已知：如图，Rt△ABC中，∠CBA＝90°，AB＝BC，Rt△DBE中，∠DBE＝90°，DB＝EB，连接DC，AE，延长AE交DC于点F．求证：（1）△AEB≌△CDB；     （2）∠CFA＝90°．                                       26．如图，在长方形中，．动点P从点B出发，沿方向以的速度向点C匀速运动；同时动点Q从点C出发，沿方向以的速度向点D匀速运动，当一个点停止运动时，另一个点也停止运动．设运动时间为．解答下列问题：（1）当点C在线段的垂直平分线上时，求t的值；（2）是否存在某一时刻t，使？若存在，求出t的值，并判断此时和的位置关系；若不存在，请说明理由；（3）设四边形的面积为，求y与t之间的关系式．