

河南省开封市通许县2023届高三三模文科数学试题A卷
展开文科数学A卷(副卷)
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上。写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是得合题目要求的.
1.设集合,,则( )
A. B. C. D.
2.在复平面内,复数对应的点的坐标为,则( )
A. B. C. D.
3.已知是定义在上的奇函数,当时,则( )
A. B.0 C.1 D.2
4.已知角的顶点为坐标原点,始边与轴的非负半轴重合,终边经过点,则( )
A. B. C. D.
5.若实数,满足约束条件,则的最大值为( )
A.5 B.9 C.10 D.12
6.现有10名象棋选手进行单循环赛(即每两名选手比赛一场).规定两人对局胜者得4分,平局各得2分,负者得0分,并按总得分由高到低进行排序.比赛结束后,10名选手的得分各不相同,且第二名的得分是最后五名选手得分之和的,则第二名选手的得分是( )
A.24 B.32 C.40 D.48
7.设甲:,乙:,则甲是乙的( )
A.充分非必要条件 B.必要非充分条件 C.充要条件 D.既非充分又非必要条件
8.某三棱锥的三视图如图所示,已知它的体积为36,则图中的值为( )
A.2 B. C.3 D.
9.对于函数,下列说法正确的是( )
①为偶函数;
②的最小正周期为;
③在区间上先减后增;
④的图象关于对称.
A.①③ B.①④ C.③④ D.②④
10.已知点是椭圆上一点,椭圆的左、右焦点分别为、,且,则的面积为( )
A.6 B.12 C. D.
11.已知函数,若,,,则,,大小关系为( )
A. B. C. D.
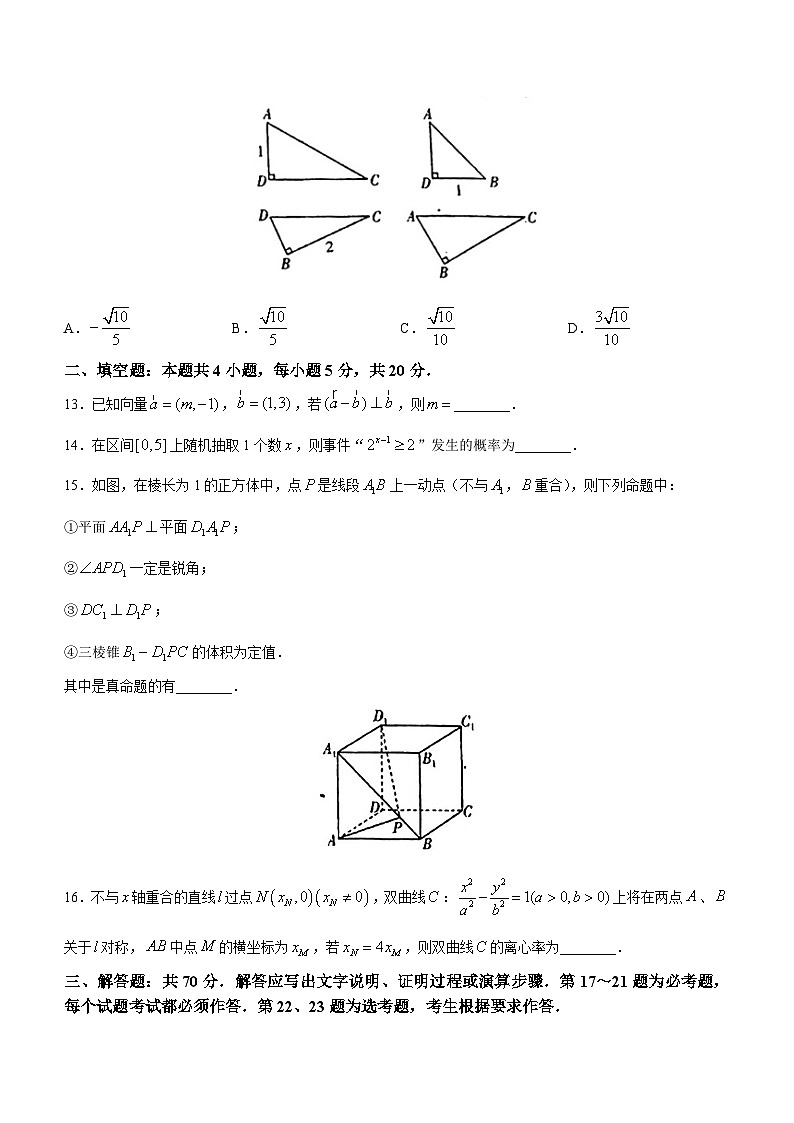
12.已知四面体的四个面均为直角三角形(如图所示),则该四面体中异面直线与所成角的余弦值为( )
A. B. C. D.
二、填空题:本题共4小题,每小题5分,共20分.
13.已知向量,,若,则________.
14.在区间上随机抽取1个数,则事件“”发生的概率为________.
15.如图,在棱长为1的正方体中,点是线段上一动点(不与,重合),则下列命题中:
①平面平面;
②一定是锐角;
③;
④三棱锥的体积为定值.
其中是真命题的有________.
16.不与轴重合的直线过点,双曲线:上将在两点、关于对称,中点的横坐标为,若,则双曲线的离心率为________.
三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考试都必须作答.第22、23题为选考题,考生根据要求作答.
(一)必考题:共60分.
17.(本小题满分12分)已知数列的首项,且满足.
(Ⅰ)证明:为等比数列;
(Ⅱ)已知为的前项和,求.
18.(本小题满分12分)如图,在四棱锥中,是边长为的正三角形,,,,,,,分别是线段,的中点.
(Ⅰ)求证:平面;
(Ⅱ)求四棱锥的体积.
19.(本小题满分12分)2022年国际篮联女篮世界杯在澳大利亚悉尼落下帷幕,中国女篮团结一心、顽强拼搏获得亚军.这届世界杯,中国女篮为国人留下了许多精彩瞬间和美好回忆,尤其是半决赛绝杀东道主澳大利亚堪称经典一幕.为了了解喜爱篮球运动是否与性别有关,某体育台随机抽取100名观众进行统计,得到如下列联表.
| 男 | 女 | 合计 |
喜爱 | 30 |
|
|
不喜爱 |
| 40 |
|
合计 |
| 50 | 100 |
(Ⅰ)将列联表补充完整,并判断能否在犯错误的概率不超过0.001的前提下认为喜爱篮球运动与性别有关?
(Ⅱ)在不喜爱篮球运动的观众中,按性别分别用分层抽样的方式抽取6人,再从这6人中随机抽取2人参加一台访谈节目,求这2人至少有一位男性的概率.
附:,其中.
0.010 | 0.005 | 0.001 | |
6.635 | 7.879 | 10.828 |
20.(本小题满分12分)已知直线与抛物线:交于,两点,且,,为垂足,点的坐标为.
(Ⅰ)求的方程;
(Ⅱ)若点是直线上的动点,过点作抛物线的两条切线,,其中,为切点,试证明直线恒过一定点,并求出该定点的坐标.
21.(本小题满分12分)已知函数,(,为常数).
(Ⅰ)当时,求函数在上的最小值;
(Ⅱ)设,是函数的两个零点,证明:.
(二)选考题:共10分.请考生在第22、23题中任选一题作答.如果多做,则按所做的第一题计分.
22.(本小题满分10分)在直角坐标系中,曲线的参数方程为(为参数),以坐标原点为极点,轴的正半轴为极轴建立极坐标系,直线的极坐标方程是.
(Ⅰ)求曲线的普通方程和直线的直角坐标方程;
(Ⅱ)设直线与曲线交于,两点,,求的值.
23.(本小题满分10分)已知,,函数的最小值为2.
(Ⅰ)求的值;
(Ⅱ)求证:.
参考答案
文科数学A卷(副卷)
1.D 【解析】∵,,
∴.故选D.
2.D 【解析】复数对应的点的坐标为,则,故.故选D.
3.A 【解析】因为是定义在上的奇函数,当时,.所以.故选A.
4.B 【解析】由题意得,所以.故选B.
5.C 【解析】由题意画出可行域,如图所示,由图可知在点处取到最大值,
联立,可得,即,所以的最大值为10.故选C.
6.B 【解析】每个选手需要进行9场比赛,则全胜的选手得分,而最后五选手之间赛10场,至少共得分,所以第二名选手至少得分.又因为10名选手的得分各不相同,若第二名选手得分34(赢了8场平1场),则第一名选手得分36分(赢9场),这时,第一全赢,第一赢了第二一局,第二输了一局,所以矛盾.不可得34分.所以第二名选手得分是32分.故选B.
7.B 【解析】当时,
则.
所以,当时,
两边都除以,得,
即,当时,不能得出,
所以由甲不一定推出乙;当时,即,
两边都乘以,得,
所以,即,
所以由乙可推出甲.所以甲是乙的必要非充分条件.故选B.
8.C 【解析】根据几何体的三视图转换为几何体为:该几何体为底面为等腰直角三角形边长为,一个侧面与底面垂直的三棱锥体.如图所示,所以,解得.故选C.
9.A 【解析】由辅助角公式可得:,
对于①.由题可知,为偶函数,①正确;
对于②,最小正周期,故②错误;
对于③,令,,在区间先减后增,复合函数同增异减易知,③正确;对于④,,所以关于点对称,④错误.故选A.
10.C 【解析】由椭圆,得,,.
设,,∴,在中,由余弦定理可得:,
可得,得,
故,故选C.
11.B 【解析】∵的定义域为,,∴为偶函数.∵,,
∴在上单调递减,∴,
∴函数在上单调递减,
又,,∴,
即,故选B.
12.C 【解析】根据已知条件可知,,,,,平面,所以四面体中平面,将四面体补成直三棱柱(如图),因为,所以(或其补角)为异面直线与所成角,在中,,,,所以,即异面直线与所成角的余弦值为,故选C.
13.13 【解析】∵,,,
又∵,∴,∴.
14. 【解析】由,得,即,∴在区间上随机抽取1个数,则事件“”发生的概率为.
15.①③④ 【解析】对于①,∵平面,∴平面平面,故①正确:
对于②,若是上靠近的一个四等分点.
,此时,.
此时为钝角;故②错;
对于③,而,,所以,且,,
所以平面,平面,因此,故③正确;
对于④,由于,则平面,
因此的底面是确定的,高也是定值,其体积为定值,故④正确.故填①③④.
16.2 【解析】设,,,则,
两式相减得,
即.
即,所以,
因为是垂直平分线,有,
所以,即,
化简得,故.
17.(Ⅰ)证明:∵,变形为,
又.
∴为等比数列,首项为1,公比为.
(Ⅱ)由(Ⅰ)可得:,
∴,
当为奇数时,;
当为偶数时,.
∴
.
18.(Ⅰ)证明:如图,取中点,连,,
??,平面.
同理,在梯形中,,平面,
∴平面平面,
又平面,∴平面;
(Ⅱ)如图,在梯形中,过作交于,
在中,得,,,
则.得,,
∴,
又,,
∴平面,
又平面,
∴平面平面,
连接,则易知,
又平面面,
∴可得平面,易知,
∴四棱锥的体积为:
.
19.解:(Ⅰ)由题意进行数据分析,得到列联表如下:
| 男 | 女 | 合计 |
喜爱 | 30 | 10 | 40 |
不喜爱 | 20 | 40 | 60 |
合计 | 50 | 50 | 100 |
计算,
所以在犯错误的概率不超过0.001的前提下认为喜爱篮球运动与性别有关;
(Ⅱ)不喜爱篮球运动的观众中,有男观众20人,女观众40人,按照分层抽样的方式抽取6人,有男观众2人,记为、,女观众4人,记为1、2、3、4,
从6人中抽取2人,有:,,,,,,,,,12,13,14,23,24,34,共15个,
记“所抽2人至少有一位男性”为事件,包含:,,,,,,,,,共9个.
所以.
20.解:(Ⅰ)设点的坐标为,点的坐标为,
因为,所以,
则直线的方程为,
联立方程组,消去,整理得,
所以有,.
又,得,
整理得,解得,
所以的方程为.
(Ⅱ)由,得,阿以,
设过点作抛物线的切线的切点为.
则相应的切线方程为,即.
设点,由切线经过点,得,
即,
设,,
则,是的两实数根,
可得,.
设是的中点,则相应,
则,
即,
又,
直线的方程为,即,
所以直线恒过定点.
21.(Ⅰ)解:令,解得,
则当时,,所以在递增;
当时,,所以在递减,
且,,
又,
所以函数在的最小值为1.
(Ⅱ)证明:不妨设,
由(Ⅰ)知,,,且,满足,
即,
由题意知,
又由(Ⅰ)可知在递减.
又,
故.而,
所以.
22.解:(Ⅰ)∵(为参数),
∴.
故曲线的普通方程为;
∵,即,
故直线的直角坐标方程为;
(Ⅱ)由(Ⅰ)得曲线的普通方程为,
直线的参数方程为(为参数).
将直线的参数方程代入曲线的普通方程并整理得,
设,对应的参数分别是,,则,,
故.
23.(Ⅰ)解:因为,,
所以,
当且仅当时等号成立,
所以的最小值为,
所以;
(Ⅱ)证明:要证,
即证,即证,
又,且,,
所以,
当且仅当,即,时等号成立,即得证.
河南省开封市通许县2023届高三三模文科数学试题A卷(Word版附解析): 这是一份河南省开封市通许县2023届高三三模文科数学试题A卷(Word版附解析),共21页。试卷主要包含了 设甲, ,下列说法正确的是等内容,欢迎下载使用。
河南省开封市通许县2023届高三冲刺(四)文科数学试题(Word版附解析): 这是一份河南省开封市通许县2023届高三冲刺(四)文科数学试题(Word版附解析),共23页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
河南省开封市杞县等4地2023届高三三模理科数学试题: 这是一份河南省开封市杞县等4地2023届高三三模理科数学试题,共10页。












