2023年广东省东莞重点学校中考数学二模试卷

这是一份2023年广东省东莞重点学校中考数学二模试卷，共20页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
2023年广东省东莞重点学校中考数学二模试卷一、选择题（本大题共10小题，共30.0分。在每小题列出的选项中，选出符合题目的一项）1.  的绝对值是(    )A.  B.  C.  D. 2.  下列图形中是轴对称图形的是(    )A.  B.  C.  D. 3.  小时候我们用肥皂水吹泡泡，泡沫的厚度约为毫米，将数据用科学记数法表示为(    )A.  B.  C.  D. 4.  下图中，不是右图所示物体从正面、左面和上面三个方向看到的图形的是(    )A.
B.
C.
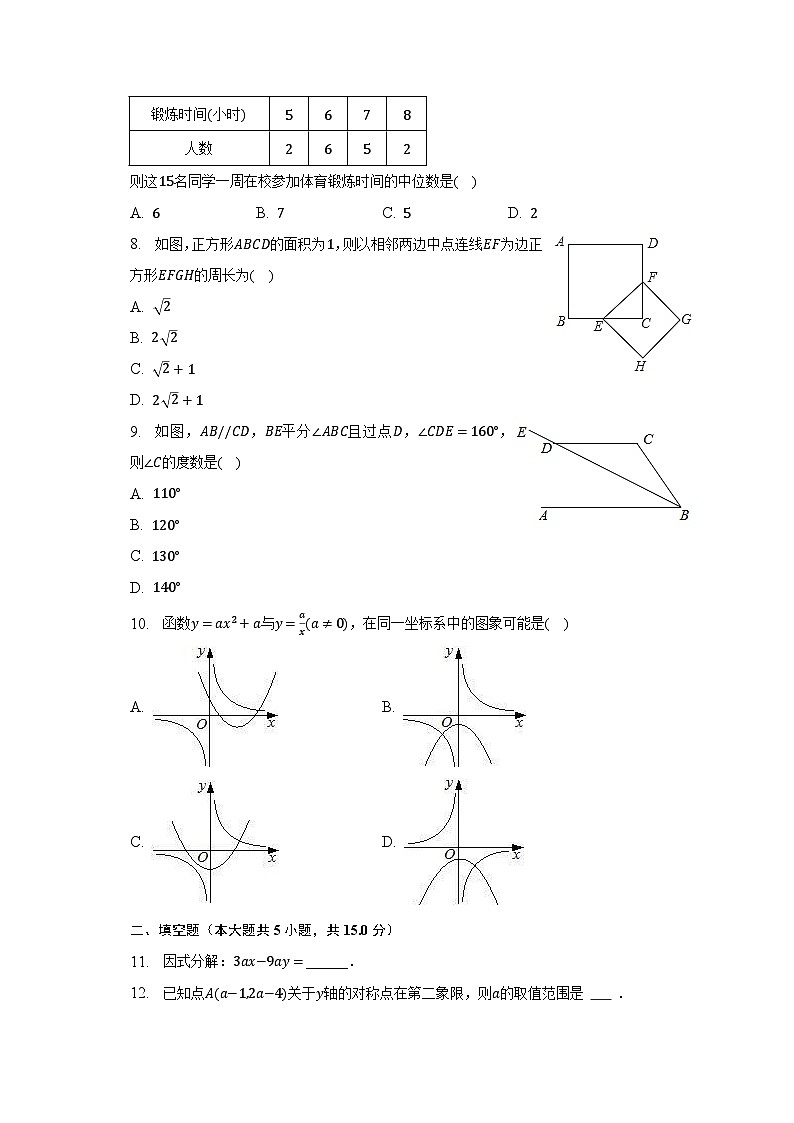
D. 5.  下列计算正确的是(    )A.  B.  C.  D. 6.  关于的一元二次方程有实数根，则的值可以是(    )A.  B.  C.  D. 7.  某中学随机调查了名学生，了解他们一周在校参加体育锻炼时间，列表如下： 锻炼时间小时人数则这名同学一周在校参加体育锻炼时间的中位数是(    )A.  B.  C.  D. 8.  如图，正方形的面积为，则以相邻两边中点连线为边正方形的周长为(    )A.
B.
C.
D. 9.  如图，，平分且过点，，则的度数是(    )A.
B.
C.
D. 10.  函数与，在同一坐标系中的图象可能是(    )A.  B.
C.  D. 二、填空题（本大题共5小题，共15.0分）11.  因式分解：______．12.  已知点关于轴的对称点在第二象限，则的取值范围是        ．13.  若一个多边形的每一个内角都是，则它的边数为______．14.  已知，则代数式的值是______．15.  如图，在中，，，，点为线段上一动点以为直径，作交于点，连，则的最小值为______ ．
三、解答题（本大题共8小题，共75.0分。解答应写出文字说明，证明过程或演算步骤）16.  本小题分
计算：．17.  本小题分
先化简，再求值：，其中．18.  本小题分
如图，是中边上一点，．

尺规作图：作的平分线，交于点保留作图痕迹，不写作法；
在的条件下，求证：．19.  本小题分
为庆祝中国共产主义青年团成立周年，某校举行了“青年大学习，强国有我”知识竞赛活动．李老师赛后随机抽取了部分学生的成绩单位：分，均为整数，按成绩划分为、、、四个等级，并制作了如下统计图表部分信息未给出：
表中______，等级对应的圆心角度数为______；
若全校共有名学生参加了此次竞赛，成绩等级的为优秀，则估计该校成绩为等级的学生共有多少人？
若等级名学生中有人满分，设这名学生分别为，，，从其中随机抽取人参加市级决赛，请用列表或树状图的方法求出恰好抽到，的概率．等级成绩分人数 
20.  本小题分
如图，在矩形中，是边上的点，，，垂足为，连接．
求证：≌；
如果，，求的值．
21.  本小题分
某农场计划建造一个矩形养殖场，为充分利用现有资源，该矩形养殖场一面靠墙墙的长度为，另外三面用栅栏围成，中间再用栅栏把它分成两个面积为：的矩形，已知栅栏的总长度为．
若矩形养殖场的总面积为，求长度；
求矩形养殖场的总面积最大值为多少．
22.  本小题分
如图，已知中，，平分，交于点，以上某一点为圆心作使经过点和点，交于点，连接并延长交的延长线于点．
判断直线与的位置关系，并说明理由；
若，，求的长；
在的条件下，求阴影区域的面积．
23.  本小题分
如图，二次函数的图象与轴交于点和点，以为边在轴上方作正方形，点是轴上一动点，连接，过点作的垂线与轴交于点．
______ ；点的坐标：______ ；
线段上是否存在点点不与、重合，使得的长为，若存在，请求出点，若不存在，请说明理由．
在轴负半轴上是否存在这样的点，使是等腰三角形？若存在，请求出点的坐标及此时与正方形重叠部分的面积；若不存在，请说明理由．


答案和解析 1.【答案】 【解析】解：的绝对值是．
故选：．
利用绝对值的意义解答即可．
本题主要考查了绝对值的意义，正确利用绝对值的意义是解题的关键．
 2.【答案】 【解析】解：、、选项中的图形都不能找到一条直线，使图形沿一条直线折叠，直线两旁的部分能够互相重合，所以不是轴对称图形；
选项中的图形能找到一条直线，使图形沿一条直线折叠，直线两旁的部分能够互相重合，所以是轴对称图形；
故选：．
根据如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形，这条直线叫做对称轴进行分析即可．
本题考查了轴对称图形的概念，轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合．
 3.【答案】 【解析】解：．
故选：．
绝对值小于的正数也可以利用科学记数法表示，一般形式为，与较大数的科学记数法不同的是其所使用的是负整数指数幂，指数由原数左边起第一个不为零的数字前面的的个数所决定．
本题考查了科学记数法的表示方法，掌握表示形式为的形式，其中，为整数是关键．
 4.【答案】 【解析】解：这个组合体的三视图如下：

故选：．
画出这个组合体的三视图，再进行判断即可．
本题考查简单组合体的三视图，理解视图的定义，掌握简单组合体三视图的画法是正确判断的前提．
 5.【答案】 【解析】直接利用合并同类项法则以及幂的乘方运算法则、同底数幂的乘法运算法则分别化简得出答案．
A、，无法计算，故此选项错误；
B、，故此选项错误；
C、，正确；
D、，故此选项错误．
故选C．
此题主要考查了合并同类项以及幂的乘方运算、同底数幂的乘法运算，正确掌握相关运算法则是解题关键．
 6.【答案】 【解析】解：方程有实数根，
，
解得：．
故选：．
根据方程的系数结合根的判别式，即可得出关于的一元一次不等式，解之即可得出的取值范围，再对照四个选项即可得出结论．
本题考查了根的判别式，牢记“当时，方程有实数根”是解题的关键．
 7.【答案】 【解析】解：这名同学一周在校参加体育锻炼时间的中位数是，
故选：．
根据中位数的定义求解即可．
本题主要考查中位数，将一组数据按照从小到大或从大到小的顺序排列，如果数据的个数是奇数，则处于中间位置的数就是这组数据的中位数．如果这组数据的个数是偶数，则中间两个数据的平均数就是这组数据的中位数．
 8.【答案】 【解析】解：正方形的面积为，
，，
、分别是、的中点，
，，
，
是等腰直角三角形，
，
正方形的周长；
故选：．
由正方形的性质和已知条件得出，，，得出是等腰直角三角形，由等腰直角三角形的性质得出的长，即可得出正方形的周长．
本题考查了正方形的性质、等腰直角三角形的判定与性质；熟练掌握正方形的性质，由等腰直角三角形的性质求出的长是解决问题的关键．
 9.【答案】 【解析】解：，
，
，
，
平分，
，
，
故选：．
首先根据邻补角互补可得，然后再根据平行线的性质可得，进而得到，即可算出的度数．
此题主要考查了平行线的性质，关键是掌握两直线平行，内错角相等．
 10.【答案】 【解析】解：当时，二次函数的图象开口向上，且对称轴为，顶点坐标为，故A、都可排除；
当时，二次函数的图象开口向下，且对称轴为，顶点坐标为，故排除，，函数的图象在二、四象限，排除，
则D正确．
故选：．
应分和两种情况分别讨论，逐一排除．
主要考查二次函数和反比例函数图象的有关性质，同学们应该熟记且灵活掌握．
 11.【答案】 【解析】解：原式．
故答案为：．
直接提取公因式即可得到答案．
此题考查的是提公因式法分解因式，找准公因式是解决此题的关键．
 12.【答案】 【解析】解：点关于轴的对称点在第二象限，
点在第一象限，
，
解得：．
故答案为：．
直接利用关于轴对称点的性质得出关于的不等式组，进而得出答案．
此题主要考查了关于轴对称点的性质，正确得出点位置是解题关键．
 13.【答案】 【解析】解：多边形每一个内角都是，
多边形每一个外角都是，
，
这个多边形的边数是．
故答案为：．
根据多边形相邻的内角与外角互为补角求出每一个外角的度数，再根据多边形的边数等于外角和除以每一个外角的度数计算即可得解．
本题考查了多边形的外角，利用多边形的边数等于外角和除以每一个外角的度数是常用的方法，求出多边形的每一个外角的度数是解题的关键．
 14.【答案】 【解析】解：因为，
所以，
则代数式，
故答案为：．
直接将已知代数式变形进而代入原式求出答案．
此题主要考查了代数式求值，正确将原式变形是解题关键．
 15.【答案】 【解析】解：如图，连接，

，
点在以为直径的上，
，
，
当点、、共线时最小，
，
，
，
的最小值为，
故答案为：．
连接，可得，从而知点在以为直径的上，继而知点、、共线时最小，根据勾股定理求得的长，即可得答案．
本题考查了圆周角定理和勾股定理，解决本题的关键是确定点运动的规律，从而把问题转化为圆外一点到圆上一点的最短距离问题．
 16.【答案】解：原式

． 【解析】直接利用负整数指数幂的性质以及特殊角的三角函数值、零指数幂的性质、二次根式的性质分别化简，进而合并得出答案．
此题主要考查了实数的运算，正确化简各数是解题关键．
 17.【答案】解：


，
当时，原式． 【解析】根据分式的加法和除法可以化简题目中的式子，然后将的值代入化简后的式子即可解答本题．
本题考查分式的化简求值，解答本题的关键是明确分式化简求值的方法．
 18.【答案】解：如图，

证明：平分，
，
，
而，
，即，
． 【解析】本题考查了作图基本作图：熟练掌握基本作图作一条线段等于已知线段；作一个角等于已知角；作已知线段的垂直平分线；作已知角的角平分线；过一点作已知直线的垂线也考查了平行线的判定．
利用基本作图作的平分线；
利用角平分线定义得到，再根据三角形外角性质得，加上，从而得到，然后根据平行线的判定方法得到结论．
 19.【答案】，；
人，
答：估计该校成绩为等级的学生共有人；
画树状图如下：

共有种等可能的结果，其中恰好抽到，的结果有种，
恰好抽到，的概率为． 【解析】解：抽取的学生人数为：人，
，等级对应的圆心角度数为：，
故答案为：，；
人，
答：估计该校成绩为等级的学生共有人；
画树状图如下：

共有种等可能的结果，其中恰好抽到，的结果有种，
恰好抽到，的概率为．
由的人数除以所占比例得出抽取的学生人数，即可解决问题；
由全校参加此次竞赛共有的人数乘以成绩为等级的学生所占比例即可；
画树状图，共有种等可能的结果，其中恰好抽到，的结果有种，再由概率公式求解即可．
此题考查的是树状图法求概率．树状图法适合两步或两步以上完成的事件；解题时要注意此题是放回试验还是不放回试验．用到的知识点为：概率所求情况数与总情况数之比．也考查了统计表和扇形统计图．
 20.【答案】证明：在矩形中，，，，
．
，，
，．
≌．

解：由知≌．
．
在直角中，，
．
在直角中，，
． 【解析】根据矩形的对边平行且相等得到，再结合一对直角相等即可证明三角形全等；
根据全等三角形的对应边相等以及勾股定理，可以求得，的长；再根据勾股定理求得的长，运用三角函数定义求解．
熟练运用矩形的性质和判定，能够找到证明全等三角形的有关条件；
运用全等三角形的性质和勾股定理求得三角形中的边，再根据锐角三角函数的概念求解．
 21.【答案】解：设，
根据题意知：较大矩形的宽为，长为 ，
，
解得或，
经检验，时，不符合题意，舍去，
，
答：此时的值为设长度为，

设矩形养殖场的总面积是，
墙的长度为，
，
根据题意得：，
，
当时，取最大值，最大值为，
答：当时，矩形养殖场的总面积最大，最大值为． 【解析】设，根据题意知：较大矩形的宽为，长为 ，可得，解方程取符合题意的解，即可得的值为；
设矩形养殖场的总面积是，根据墙的长度为，可得，根据题意得出函数解析式，由二次函数性质求最值．
本题考查一元二次方程和二次函数的应用，解题的关键是读懂题意，列出方程及函数关系式．
 22.【答案】证明：直线与相切，理由如下：
如图，连接，

平分，
，
，
，
，
，
，
，
，
是的切线；
解：是直径，
，
，
平分，，
，
，
，
在中，，
，
，
，
∽，
，
，
，
，
，
，
，
在中，，
，
；
解：，，，
，
，
，
，
，
． 【解析】连接，根据角平分线的定义得出，由等边对等角得出，即可得出，进而判定，根据平行线的性质得到，即，即可得解；
由是直径得出，进而得到，，根据两角相等的两个三角形相似得到∽，即可得出，求出，在根据锐角三角函数定义求出，即得，再根据直角三角形中的角所对的直角边等于斜边的一半得出，即可根据求解；
根据阴影部分面积等于的面积减去扇形的面积求解即可．
此题是圆的综合题，考查了切线的判定与性质、锐角三角函数、相似三角形的判定与性质、勾股定理等知识，熟记相关的定理及证明直线与相切是解题的关键．
 23.【答案】   【解析】解：点在二次函数的图象上，
，
解得：，
二次函数解析式为，
点，，
四边形为正方形，
，
点，
故答案为：；．

线段上存在点点不与、重合，使得的长为．

假设存在点，使得的长为，设，则，
，，
，
在中，，
在中，，
，即，
解得：或；
点的坐标为或；
故线段上存在点或，使得的长为；

在轴负半轴上存在这样的点，使是等腰三角形．
假设是等腰三角形，交轴于点，如图，

是等腰三角形，
，
，四边形为正方形，
，，，
，，
在和中，
，
≌，
，，
点坐标为．
轴，
，
两直线平行，内错角相等，
又对顶角，
∽，
，
，
，
与正方形重叠部分面积为：．
答：存在这样的点，点的坐标为，此时与正方形重叠部分的面积为．
利用点在二次函数图象上，代入即可求得，将二次函数换成交点式，即能得出点的坐标，由可算出点坐标；
假设线段上存在点点不与、重合，使得的长为直线交轴于点，设，则，由，找出，利用两角的正切相等得到一元二次方程，解得或，从而得到的长度以及点的坐标；
图中，交轴于点，利用角和边的关系，得到≌，再利用∽，借助相似比即可求得，求出的面积即是所求．
本题考查了二次函数的交点式、全等三角形的判定、相似三角形的相似比等知识，解题的关键是注重数形结合，找准等量关系．