2023年河北省保定市高碑店市中考三模数学试题（含答案）

这是一份2023年河北省保定市高碑店市中考三模数学试题（含答案），共18页。试卷主要包含了5°C．55°D．52，4分． ………………6分等内容，欢迎下载使用。

2023年河北省初中毕业生升学文化课模拟考试（三）
数学试卷 2023.6
【命题：河北启光教育科技有限公司】
注意事项：
1．本试卷共8页，总分120分，考试时间120分钟．
2．答题前，考生务必将姓名、准考证号填写在试卷和答题卡的相应位置．
3．所有答案均在答题卡上作答，在本试卷或草稿纸上作答无效．答题前，请仔细阅读答题卡上的“注意事项”，按照“注意事项”的规定答题．
4．答选择题时，用2B铅笔将答题卡上对应题目的答案标号涂黑；答非选择题时，请在答题卡上对应题目的答题区域内答题．
5．考试结束时，请将本试卷和答题卡一并交回．
一、选择题（本大题共16个小题，共42分．1～10小题各3分；11～16小题各2分．在每小题给出的四个选项中，只有一项是符合题目要求的）
1．与（，均不为0）的积为1的是（ ）
A． B． C． D．
2．下列正确的是（ ）
A． B．
C． D．
3．下列正多边形中的一个外角等于60°的是（ ）
A． B． C． D．
4．因式分解“”得，则“？”是（ ）
A． B． C． D．
5．如图，小雨要用一个长方形纸片折叠一个小兔子，第一步沿折叠，使点落到边上的点处，若，则（ ）

A．65° B．62.5° C．55° D．52.5°
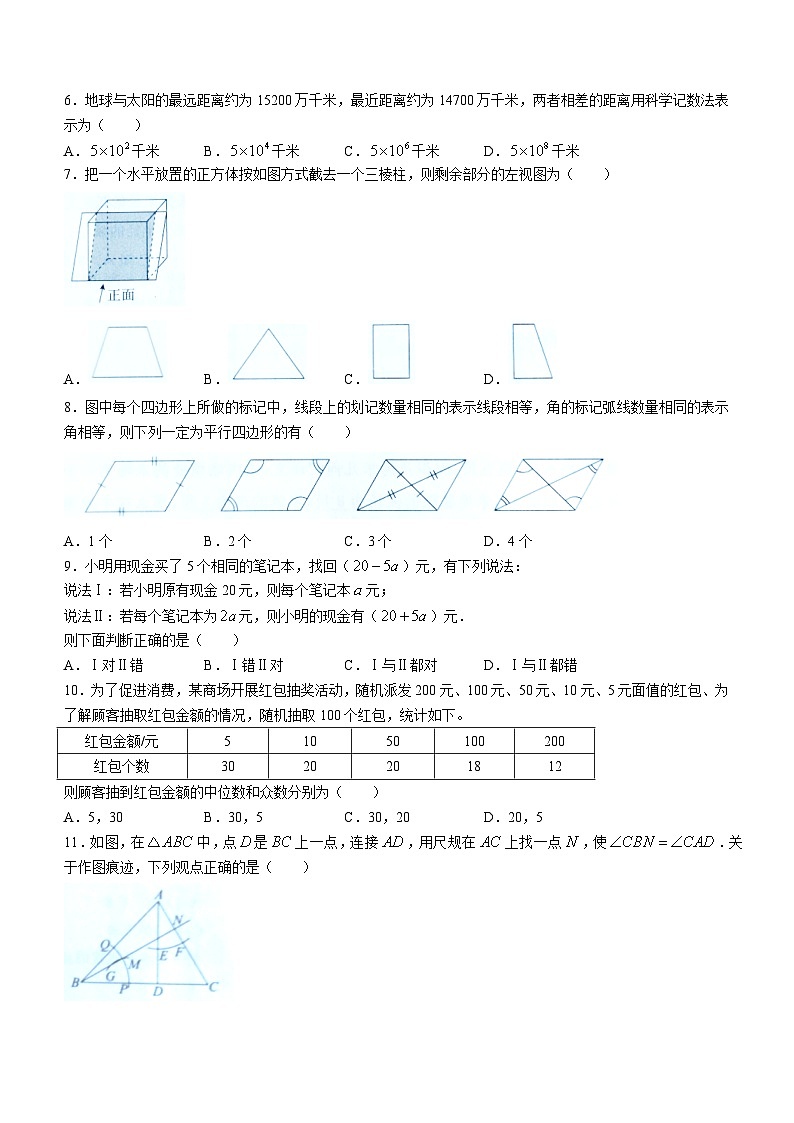
6．地球与太阳的最远距离约为15200万千米，最近距离约为14700万千米，两者相差的距离用科学记数法表示为（ ）
A．千米 B．千米 C．千米 D．千米
7．把一个水平放置的正方体按如图方式截去一个三棱柱，则剩余部分的左视图为（ ）

A． B． C． D．
8．图中每个四边形上所做的标记中，线段上的划记数量相同的表示线段相等，角的标记弧线数量相同的表示角相等，则下列一定为平行四边形的有（ ）

A．1个 B．2个 C．3个 D．4个
9．小明用现金买了5个相同的笔记本，找回（）元，有下列说法：
说法Ⅰ：若小明原有现金20元，则每个笔记本元；
说法Ⅱ：若每个笔记本为元，则小明的现金有（）元．
则下面判断正确的是（ ）
A．Ⅰ对Ⅱ错 B．Ⅰ错Ⅱ对 C．Ⅰ与Ⅱ都对 D．Ⅰ与Ⅱ都错
10．为了促进消费，某商场开展红包抽奖活动，随机派发200元、100元、50元、10元、5元面值的红包、为了解顾客抽取红包金额的情况，随机抽取100个红包，统计如下。
红包金额/元
5
10
50
100
200
红包个数
30
20
20
18
12
则顾客抽到红包金额的中位数和众数分别为（ ）
A．5，30 B．30，5 C．30，20 D．20，5
11．如图，在中，点是上一点，连接，用尺规在上找一点，使．关于作图痕迹，下列观点正确的是（ ）

A．是以点为圆心、长为半径的弧
B．是以点为圆心、长为半径的弧
C．是以点为圆心、长为半径的弧
D．是以点为圆心、长为半径的弧
12．对于二次函数，已知，当时，有下列说法：
①若的最大值为，则；
②若的最小值为，则；
③若，则的最大值为．
则上达说法（ ）
A．只有①正确 B．只有②正确 C．只有③正确 D．均不正确
13．《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题：“今有委米依垣内角，下周八尺，高五尺，问积及为米几何？”译文：屋内墙角处的米堆为一个圆锥的四分之一（如图），米堆底部的弧长为8尺，米堆的高为5尺，那么这个米堆遮挡的墙面面积为（ ）

A．平方尺 B．平方尺 C．平方尺 D．平方尺
14．平面内，将长分别为2，4，3的三根木棒按如图方式连接成折线，其中可以绕点任意旋转，保持，将，两点用绷直的皮筋连接，设皮筋长度为，则不可能是（ ）

A．3 B．5 C．7 D．8
15．已知数轴上两点，表示的数分别为，1，那么关于的不等式的解集，下列说法正确的是（ ）
A．若点在点左侧，则解集为
B．若点在点右侧，则解集为
C．若解集为，则点必在点左侧
D．若解集为，则点必在点右侧
16．如图，在中，，点为上一点，以5为半径作分别与，相切于，两点，与交于点，连接交于点，连接，，若点为的中点，给出下列结论：①平分；②点为的中点；③；④的长度为．其中正确结论的个数是（ ）

A．1 B．2 C．3 D．4
二、填空题（本大题共3个小题，每小题3分，共9分，其中18小题第一空2分，第二空1分；19小题每空1分）
17．若与互为相反数，则______．
18．将正方体的一种展开图按如图方式放置在直角三角形纸片上，若小正方形的边长为1，则

（1）______；
（2）______．
19．有大小不同的两个正方形A，B，把正方形B按照如图1所示的方式放到正方形A中，阴影部分的面积为，且小于正方形B的面积．

图1 图2
（1）正方形A比B的边长大______cm；
（2）把正方形A，B按照如图2所示的方式放到正方形C中，固定正方形A的位置，正方形B可以在剩余位置平移，连接正方形A，B右下角的顶点所得线段的长度为，的最大值为．
①正方形A，B的面积之和为______；
②正方形C的边长为______ cm．
三、解答题（本大题共7个小题，共69分．解答应写出文字说明、证明过程或演算步骤）
20.（本小题满分9分）
按照如图所示的程序，进行计算．
（1）如果输入，求输出结果；
（2）若在图1基础上增加一个计算程序“”，如图2，重新输入，第一次运算得到，求输出结果．

图1 图2
21．（本小题满分9分）
甲、乙地人分别以，作为起始整式，第一次分别用自己的整式减去对方整式的2倍，得到新的整式；以后每次都用自己得到的整式分别减去对方得到整式的2倍．如下表所示：

甲
乙
甲、乙所得整式的差
起始整式



第一次操作



第二次操作



…
…
…
…
（1）写出代表的整式，并化简；
（2）求第二次操作后甲、乙所得整式的差；
（3）请直接写出第四次操作后甲、乙所得整式的差．
22．（本小题满分9分）
某校有甲、乙两个辩论队，每队各有10名队员，学校对这20名队员进行了专业素养和综合素养测试（满分均为10分），测试成绩如图所示．

（1）队员D的专业素养得分为______分，综合素养得分为______分；
（2）将专业素养、综合素养分别按60%，40%计算每名队员的最终成绩，求队员D的最终成绩；
（3）学校要从这两个辩论队专业素养和综合素养的成绩都高于8分的队员中，随机选择两名学生作为领队，求被抽选到的两名队员来自同一辩论队的概率．（用画树状图或列表法）
23．（本小题满分10分）
如图，水平放置的平台高度为1 dm，平台上的光源和竖直放置的屏幕都可以左右平移，但光源的照射角度和方向不变，，平台左端是竖直放置的平面镜，没有屏幕遮挡，从点发射的光线会照射到平面镜的点处；若屏幕与平面镜相距1 dm，则光线照射到屏幕上的点处．以1 dm为1个单位长度建立平面直角坐标系，点，的坐标分别为，．

（1）在图中画出平面直角坐标系，并求光线所在直线的解析式及点的坐标；
（2）将屏幕向右平移到与平面镜相距6 dm的处，若使光线经平面镜反射后恰好照射到顶端，求光源的平移方向和距离．
24．（本小题满分10分）
如图，将一把刻度尺（单位：cm）紧贴玻璃杯外壁上的点，用一个简易的“V”字型夹子夹紧玻璃杯外壁（即与外壁相切），已知夹子的两个夹持片，端点，在刻度尺上所对应的刻度分别为5和15，点与点正对且相距12 cm．

（1）求点对应的刻度值；
（2）设夹持片与玻璃杯外壁的接触点为，求这只玻璃杯的外径（外壁的直径）．
25．（本小题满分10分）
如图，抛物线（）经过点，过点作轴，向右作，且，以，为邻边构造矩形．双曲线在第一象限内的分支：经过的中点．

（1）用含的代数式表示，并求双曲线的解析式（不写自变量的取值范围）；
（2）若抛物线经过点，求抛物线的解析式，并求第一象限内两个函数图象围成的封闭区域内（包括边界）所有整点（横、纵坐标都是整数的点）的个数；
（3）若在图象的上方，抛物线与矩形的边有2个公共点，直接写出的取值范围．
26．（本小题满分12分）
菱形的边长为6 cm，，，，分别在边，，上，．点从点出发，沿折线以1 cm/s的速度匀速运动，到达点时停止．连接，作，射线与菱形的另一边交于点，如果与对角线有交点，设交点为．如图1，当点位于起始位置点处时，，设点的运动时间为．

图1 图2 图3
（1）求的长度；
（2）用含的式子表示点到的距离（写出的取值范围）；
（3）如图2，若点在上运动，则当为何值时最大？求出最大值，并判断此时与的数量关系；
（4）直接写出点不在外部的总时长．



2023年河北省初中毕业生升学文化课模拟考试（三）
数学试题参考答案及评分参考 2023.6
说明：
1．在阅卷过程中，如考生还有其他正确解法，可参照评分标准按步骤的情给分．
2．坚持每题评阅到底的原则，当考生的解答在某一步出现错误，影响了后继部分时，如果该步以后的解答未改变这一题的内容和难度，可视影响的程度决定后面部分的给分，但不得超过后继部分应给分数的一半；如果这一步后面的解答有较严重的错误，就不给分．
3．解答右端所注分数，表示正确做到这一步应得的累加分数，只给整数分数．
一、选择题（本大题共16个小题，共42分．1～10小题各3分；11~16小题各2分．在每小题给出的四个选项中，只有一项是符合题目要求的）
题号
1
2
3
4
5
6
7
8
答案
A
C
D
D
B
C
D
C
题号
9
10
11
12
13
14
15
16
答案
C
B
B
C
A
D
C
D
1．解析：由倒数的定义知，与的积为1的是．故选A．
2．解析：，故A不正确；，故B不正确；，故C正确；，故D不正确，故选C．
3．解析：正六边形的一个外角，故选D．
4．解析：∵，∴“？”是，故选D．
5．解析：∵，∴，∴．
由折叠可知，，故选B．
6．解析：∵15200万14700万500万5000000（千米），
∴两者相差的距离用科学记数法表示为千米．故选C．
7．解析：正方体按图中方式截去一个三棱柱后，剩余部分为一个四棱柱，且底面为直角梯形，故剩余部分的左视图为直角梯形，故选D．
8．解析：由第四个图形中的两组对角分别相等，得到的只有一组对边平行，故不能判断该四边形是平行四边形，其他三个图形均可判断为平行四边形，故选C．
9．解析：由题意可知，若小明原有现金20元，找回（）元，则5个笔记本为元，每个笔记本元；若每个笔记本为元，则5个笔记本为元，原有现金元，故Ⅰ与Ⅱ都对，故选C．
10．解析：因为顾客抽到红包的第50个和第51个数分别是10和50，故顾客抽到红包金额的中位数是，众数是5，故选B．
11．解析：根据作一个角等于已知角，可得是以点为圆心、长为半径的弧，故A错误；是以点为圆心、长为半径的弧，故C，D错误，故选B．
12．解析：二次函数图象的对称轴为直线．
因为，所以当时，函数单调递增．
若的最大值为，则，解得或（舍去），故①错误；
若的最小值为，则，解得或，此时不存在，故②错误；
若，则，所以的最大值为，故③正确，故选C．
13．解析：设米堆底部的扇形半径为，则由米堆底部的弧长为8尺，可得，解得，所以这个米堆遮挡的墙面面积为（平方尺），故选A．
14．解析：连接，则．
如图1，当点在线段上时，；

如图2，当点在的延长线上时，，
∴的取值范围为，故选D．
15．解析：关于的不等式化为，当时，解集为，此时点在原点左侧，故A，B，D选项错误，C选项正确，故选C．
16．解析：如图，连接，．

∵分别与和相切，∴，且，，
∴圆心在的平分线上，故①正确；
∵点为的中点，∴，∴，
由①有，∴，∴点为的中点，
∴，故点为的中点，故②正确；
由①知，，∴，
∴，故③正确；
由③可知，∴的长度为，故④正确，故选D．
二、填空题（本大题共3个小题，每小题3分，共9分，其中18小题第一空2分，第二空1分：19小题每空1分）
17． 解析：∵与互为相反数，∴，∴，
∴．
18．（1） （2）8
解析：（1）如图，∵，∴，

在中，，∴．
（2）∵，∴．
∵，，∴≌（ASA）．
∴，．
∵，∴．
19．（1）2 （2）①52 ②10
解析：设正方形A，B的边长分别为，．
（1）由题意，得，所以，即正方形A比B的边长大2 cm，
（2）①当正方形B在如图所示的位置时，取最大值．
由勾股定理，得．
②由，得，∴，即，
∴，
∴正方形C的边长为．

三、解答题（本大题共7个小题，共69分）
20．解：（1）由题意：得
………………2分
， ………………4分
∵，∴输出结果为1．
（2）由题意，得，故． ………………7分
∵，
∴进行第二次运算：，
∴输出结果为24．
21．解：（1） ………………2分

． ………………4分
（2） ………………6分

． ………………8分
（3）． ………………9分
22．解：（1）5，6 ………………8分
（2）根据题意，可得（分），
∴队员D的最终成绩为5.4分． ………………6分
（3）从统计图可以看出，甲、乙两个辩论队专业素养和综合素养的成绩都高于8分的队员均为2名，分别设为A，B，a，b，现从中随机抽取两名队员，列表如下：

A
B
a
b
A
—



B

—


a


—

b



—
从4名队员中随机抽取两名队员，共有12种等可能的结果，其中两名队员是同一辩论队有4个等可能的结果，则（来自同一辩论队）． ………………9分
23．解：（1）平面直角坐标系如图所示． ………………2分
设光线所在直线的解析式为，
把，代入，得 解得
∴直线的解析式为． ………………5分
当时，，
∴点的坐标为． ………………7分

（2）由题意，得．
如图，作点关于轴的对称点，过点作，交平台于点，由光的反射定律可知，点为光源位置． ………………8分
设所在直线的解析式为，
把代入，得，解得，
∴直线的解析式为． ………………9分
当时，由，解得，
∴光源要向左平移，平移距离为． ………………10分
24．解：（1）如图，连接．

由题意得，，，都是的切线，，经过点，
又∵，∴为的中点．
∵，∴，
即点对应的刻度为． ………………4分
（2）如上图，连接，设的半径为，则．
∵，，
∴∽， ………………5分
∴， ………………7分
∴，解得． ………………9分
∴这只玻璃标的外径为． ………………10分
25．解：（1）将点的坐标代入抛物线的解析式，得，
∴． ………………2分
∵轴，，，点为的中点，∴，．
把代入，得，则，
∴双曲线的解析式为． ………………4分
（2）∵矩形中，，，
∴，．
由（1）得，抛物线的解析式可以表示为（）．
把代入，得，解得．
∴抛物线的解析式为． ………………6分
当时，，∴抛物线经过点，
同理，抛物线经过点． ………………8分
∵图象经过，，且点，在上方，
∴符合题意的整点坐标分别为，，，，，，共有7个． ………………9分
【解法提示】7个整点的位置如图所示：

（3）的取值范围为或． ………………10分
解析：在原题图形状态下，随着的减小，抛物线的开口变小，顶点下移．
①当抛物线经过点时，由（2）可知，也经过点，则在图象的上方，抛物线与矩形的边有2个公共点，此时；
②当抛物线的顶点在上时，由，解得，（不合题意，舍去），此时符合题意的公共点有3个，随着的减小，公共点变为2个；
③当抛物线经过点时，则，解得，此时符合题意的公共点有1个．
综上可知，的取值范围为或．
26．解：（1）菱形中，，
∴∽，∴，∴． ………………1分
∵，∴，∴四边形为平行四边形，
∴，∴．
∵，∴，即． ………………3分
（2）当点在上时，如图1，过点作，垂足为，
则，，
∴，，
即（）； ………………5分
当点在上时，如图2，
∵，∴到的距离等于两条平行线、之间的距离，
过点作，垂足为，
则，，即（）； ………………6分
当点在上时，如图3，过点作，垂足为，
则，，
∴，
即（）． ………………7分

（3）菱形中，，，
∴是等边三角形，∴，∴．
∵，∴．
又∵，∴，
∴∽，∴．
∴，∴， ………………8分
∴当时，有最大值，最大值为． ………………8分
如图4，连接，则等边三角形中，，

∴，即．
∵∽，∴．
在与中，，，，
∴≌，∴． ………………11分
（4） ………………12分
解析：当点在折线上运动时，点始终在的内部．
当时，同理可得，
当时，，解得，．
∵点不在外部，包括点在的内部或边上两种情况，
∴点不在外部的总时长．