四川省乐山市沫若中学2021-2022学年高二数学（文）下学期第二次月考试题（Word版附解析）

2021级高二下5月月考数学试卷（文）

一、单选题（每题5分，总计60分）

1. 复数 (为虚数单位)在复平面内表示的点的坐标为

A.  B.  C.  D.

【答案】A

【解析】

【详解】分析：求出复数的代数形式，再写出在复平面内表示的点的坐标．

详解：复数，所以复数在复平面内表示的点的坐标为，选A.

点睛：本题主要考查了复数的四则运算，以及复数在复平面内所表示的点的坐标，属于容易题．

2. 命题“”的否定是（    ）

A.  B.  C.  D.

【答案】C

【解析】

【分析】由全称命题否定：任意改存在并否定结论，即可得答案.

【详解】由全称命题的否定为特称命题，

所以，原命题的否定为.

故选：C

3. 函数的单调递增区间是（    ）

A.  B.  C.  D.

【答案】C

【解析】

【分析】利用导数研究函数的单调区间即可.

【详解】由，故时，时，

所以时递减，时递增，

综上，的递增区间为.

故选：C

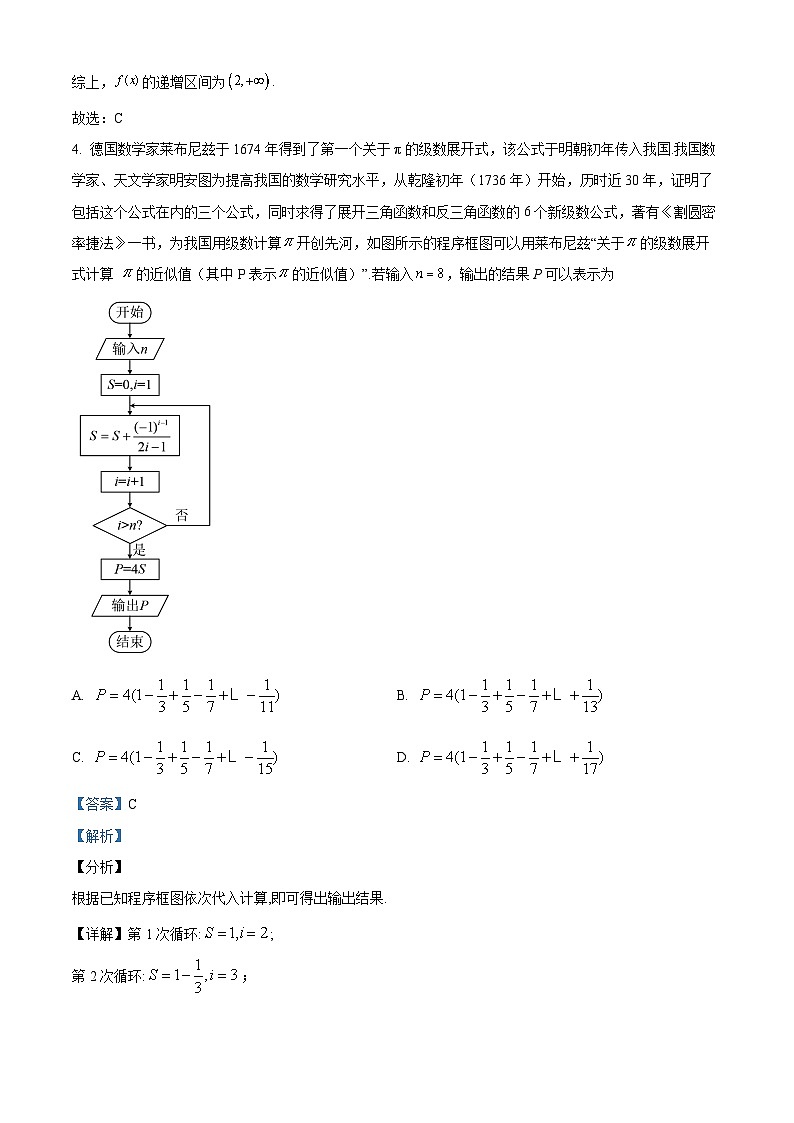
4. 德国数学家莱布尼兹于1674年得到了第一个关于π的级数展开式，该公式于明朝初年传入我国.我国数学家、天文学家明安图为提高我国的数学研究水平，从乾隆初年（1736年）开始，历时近30年，证明了包括这个公式在内的三个公式，同时求得了展开三角函数和反三角函数的6个新级数公式，著有《割圆密率捷法》一书，为我国用级数计算开创先河，如图所示的程序框图可以用莱布尼兹“关于的级数展开式计算 的近似值（其中P表示的近似值）”.若输入，输出的结果P可以表示为

A.  B.

C.  D.

【答案】C

【解析】

【分析】

根据已知程序框图依次代入计算,即可得出输出结果.

【详解】第1次循环:;

第2次循环:；

第3次循环: ;

…

第8次循环: ,

此时满足判定条件,输出结果.

故选:C

【点睛】本题主要考查了循环结构的程序框图的计算与输出,其中解答中认真审题,逐次计算,得到程序框图的计算功能是解答的关键,着重考查了分析问题和解答问题的能力,属于基础题

5. 我国古代典籍《周易》用“卦”推测自然和社会的变化，如图是一个八卦图，包含乾、坤、震、巽、坎、离、艮、兑八卦、分别象征着天、地、雷、风、水、火、山、泽八种自然现象.每一卦由三个爻组成，其中“▃”表示一个阳爻，“▃▃”表示一个阴爻）.若从含有两个或两个以上阴爻的卦中任取两卦，这两卦中恰好含有两个阳爻的概率是（    ）

A.  B.  C.  D.

【答案】B

【解析】

【分析】首先写出所有情况为6种，再得到其中满足题意的情况，最后即可得到概率.

【详解】含有两个或两个以上阴爻的卦有坎、艮、震、坤卦，若任取两卦则有种，

其中恰好含有两个阳爻的有坎卦与艮卦；坎卦与震卦；艮卦与震卦共3种，
故概率为，

故选：B.

6. 已知：，那么命题的一个必要非充分条件是（    ）

A.  B.

C.  D.

【答案】B

【解析】

【分析】先解不等式求出，然后结合选项根据必要不充分条件的概念即可判断.

【详解】因为，所以，然后结合选项根据必要不充分条件的概念可判断，

故选：B.

7. 已知甲、乙两名同学在高三的6次数学测试成绩统计的折线图如下，下列说法正确的是（    ）

A. 若甲、乙两组数据的方差分别为，，则

B. 甲成绩比乙成绩更稳定

C. 甲成绩的极差大于乙成绩的极差

D. 若甲、乙两组数据的平均数分别为，，则

【答案】B

【解析】

【分析】根据题中折线图的数据信息以及变化趋势，结合平均数、方差和极差的定义逐项分析判断

【详解】对A、B：由折线图的变化趋势可知：甲的成绩较为集中，乙成绩波动很大，故甲成绩比乙成绩更稳定，故，故A错误，B正确；

对C：极差为样本的最大值与最小值之差，甲的极差大约为30，乙的极差远大于30，故甲的极差小于乙的极差，C错误；

对D：由图可知：甲的成绩除第二次略低于乙的成绩，其余均高于乙的成绩，故，D错误；

故选：B.

8. 若f′(x0)＝，则 等于（    ）

A. －1 B. －2 C. 1 D. 2

【答案】D

【解析】

【分析】利用导数的定义求解,

【详解】解：因为f′(x0)＝，

所以 ，

故选：D

9. 函数在区间的图像大致为（    ）

A.  B.

C.  D.

【答案】B

【解析】

【分析】先根据函数解析式判断函数的奇偶性，发现是奇函数，排除C、D；观察A、B两项，发现图像在处的增减趋势不同，所以对函数进行求导，再把特殊值代入导函数中判断即可.

【详解】因为，所以是奇函数，排除C、D两项；

当时，，则，

所以，

所以在处的切线斜率为负数，故排除A项；

故选：B.

10. 已知是区间内任取的一个数，那么函数在上是增函数的概率是（　　）

A.  B.  C.  D.

【答案】C

【解析】

【分析】首先得到恒成立，则解出的范围，再根据其在内取数，利用几何概型公式得到答案.

【详解】，

在上是增函数

恒成立

解得或

又是区间内任取的一个数

由几何概型概率公式得

函数在上是增函数的概率

故选：C．

11. 已知函数存在两个零点，则实数t的取值范围为（    ）

A.  B.  C.  D.

【答案】C

【解析】

【分析】将问题转化为有两个不同的实数根，构造函数利用导数求解单调性即可求解最值.

【详解】存在两个零点，则有两个不同的实数根，

当时，只有一个零点，不符合题意，故，

即有两个不同的实数根，

记，

当时，，此时单调递减，当时，，此时单调递增，故当时，取极大值也是最大值，

又当时，，如图为的图象

要使有两个不同的实数根，则，所以，

故选：C

12. 已知是偶函数的导函数，．若时，，则使得不等式成立的x的取值范围是（    ）

A.  B.

C.  D.

【答案】C

【解析】

【分析】设，求导得，进而可得时，单调递增，由于为偶函数，推出为奇函数，进而可得在上单调递增，由于，则，由于，则，推出，即可得出答案．

【详解】设，，

由题意得时，，单调递增，

因为为偶函数，所以，

所以，

所以为奇函数，所以在上单调递增，

因为，所以，

因为，所以，

所以，所以，

故选：C．

二、填空题（每题5分，总计20分）

13. 已知，则_____．

【答案】

【解析】

【分析】先求出，令后可得的值．

【详解】，令，

则，故．填．

【点睛】本题考查函数导数的运算，属于容易题，求导时注意为常数．

14. 为庆祝中国共产党第二十次代表大会胜利闭幕，某高中学校在学生中开展了“学精神，悟思想，谈收获”二十大精神宣讲主题活动．为了解该校学生参加主题学习活动的具体情况，校团委利用分层抽样的方法从三个年级中抽取了260人进行问卷调查，其中高一、高二年级各抽取了85人．已知该校高三年级共有720名学生，则该校共有学生______人．

【答案】

【解析】

【分析】根据题意求得每个学生抽到的概率，结合分层抽样列出方程，即可求解.

【详解】利用分层抽样的方法从三个年级中抽取了260人进行问卷调查，其中高一、高二年级各抽取了85人，可得高三年级共有90人，

又由高三年级共有720名学生，则每个学生被抽到的概率为，

设该校共有名学生，可得，解得（人），

即该校共有名学生.

故答案为：.

15. 已知，对，且，恒有，则实数的取值范围是__________.

【答案】

【解析】

【分析】根据对条件 做出的解释构造函数，利用函数的单调性求解.

【详解】对，且，恒有，即 ，所以函数 是增函数，

设 ，则在上单调递增，故 恒成立，

即，设 ，

当时， ，函数单调递增；当时， ，函数单调递减；

故，即；

故答案为： .

16. 如图所示，在等腰直角三角形ABC中，∠C为直角，BC=2，EF∥BC，沿EF把面AEF折起，使面AEF⊥面EFBC，当四棱锥A-CBFE的体积最大时，EF的长为__．

【答案】##

【解析】

【分析】由题意推出AE⊥平面BCEF，设EF=x，则AE＝x，EC＝2-x，表示出四棱锥A﹣CBFE的体积，利用导数求其最值，即可得答案.

【详解】由题意可知AEC是等腰直角三角形，

EF∥BC，沿EF把面AEF折起，使面AEF⊥面EFBC， ,

平面AEF平面EFBC=EF，平面AEF,故AE⊥平面BCEF，

设EF=x，则AE＝x，EC＝2-x，

四棱锥A﹣CBFE的体积：V，（），

，由 ，解得x，

当x∈(0，)时，，当x∈(，2)时，,

∴当时，四棱锥A﹣CBFE的体积最大，即EF的长为．

故答案为：．

三、解答题（17题10分，其余各题12分，总计70分）

17. 已知函数在处取得极大值.

（1）求的值；

（2）当时，求的最大值.

【答案】（1）   

（2）5

【解析】

【分析】（1）求导得，根据函数极值与导数的关系得到关于方程组，解出并检验即可；

（2）直接求导，列出函数与导函数变化的表格，通过表格即可求出最大值.

【小问1详解】

，且函数在处有极值1，

，解得.                            

又当时，

当或时，，

当时，，

故在处取得极大值，满足题意.

综上，.

【小问2详解】

当，时，．则．

当变化时，与的变化情况如下表：

所以时，的最大值为.

18. 近几年，在缺“芯”困局之下，国产替代的呼声愈发高涨，在国家的政策扶持下，国产芯片厂商呈爆发式增长．为估计某地芯片企业的营业收入，随机选取了10家芯片企业，统计了每家企业的研发投入（单位：亿）和营业收入（单位：亿），得到如下数据：

并计算得，，，，．

（1）求该地芯片企业研发投入与营业收入的样本相关系数r，并判断这两个变量的相关性强弱（若，则线性相关程度一般，若，则线性相关程度较高，r精确到0.01）；

（2）现统计了该地所有芯片企业的研发投入，并得到所有芯片企业的研发投入总和为268亿，已知芯片企业的研发投入与营业收入近似成正比．利用以上数据给出该地芯片企业的总营业收入的估计值．

附：相关系数，．

【答案】（1），两个变量线性相关程度较高   

（2）该地芯片企业的总营业收入的估计值为亿元．

【解析】

【分析】（1）由条件数据求，利用关系，

，求值，代入公式求相关系数即可；

（2）设该地芯片企业的总营业收入的估计值为m，由条件，列关系式求即可.

【小问1详解】

因为，，

所以，，又，，，

所以，

，

，

所以，

故两个变量线性相关程度较高．

【小问2详解】

设该地芯片企业的总营业收入的估计值为m，

则，解得，

所以该地芯片企业的总营业收入的估计值为亿元．

19. 某学校有学生人，为了解学生对本校食堂服务满意程度，随机抽取了名学生对本校食堂服务满意程度打分，根据这名学生打分，绘制频率分布直方图（如图所示），其中样本数据分组区间为.

（1）求频率分布直方图中的值，并估计该校学生满意度打分不低于分的人数；

（2）若采用分层抽样的方法，从打分在的受访学生中随机抽取人了解情况，再从中选取人进行跟踪分析，求这人至少有一人评分在的概率.

【答案】（1） ，680人   

（2）

【解析】

【分析】（1）由频率分布直方图中所有小矩形的面积之和为得到方程，即可求出，再估计出满意度打分不低于分的人数；

（2）首先求出打分在和内人数，再用列举法列出所有可能结果，最后根据古典概型的概率公式计算可得.

【小问1详解】

由频率分布直方图可知，，

解得.

该校学生满意度打分不低于分的人数为 .

【小问2详解】

由频率分布直方图可知，打分在和内的频率分别为和，
抽取的人采用分层抽样的方法，在内的人数为人，在内的人数为人.
设内的人打分分别为，，内的人打分分别为，，，
则从的受访学生中随机抽取人，人打分的基本事件有：

，，共种.
其中两人都在内的可能结果为，
则这人至少有一人打分在的概率.

20. 如图，在直三棱柱中，，D为的中点，为上一点，且．

（1）证明：∥平面；

（2）若，，求点到平面距离．

【答案】（1）证明见解析；   

（2）.

【解析】

【分析】（1）如图，连接交于点，连接，证明，原题即得证；

（2）由题知点到平面的距离等于点到平面的距离的一半，过作，垂足为，连接，过作，垂足为，先证明平面，即线段为点到平面的距离，再求出即得解.

小问1详解】

如图，连接交于点，连接，

因为四边形为矩形，且为的中点，所以，

又因为，所以，所以，

因为平面，平面，所以平面．

【小问2详解】

由题知点到平面的距离等于点到平面的距离的一半，

过作，垂足为，连接，过作，垂足为，

因为平面，平面，所以，

又因为，平面，平面，

所以平面，

因为平面，所以.

又平面，，

所以平面，即线段为点到平面的距离．

因为，，，所以，

由几何关系可知，

所以，，

由几何关系可知，

所以，故点到的距离为．

21. 设函数．

（1）若，求的单调区间；

（2）若对任意，都有，求实数的取值范围．

【答案】（1）单调递减区间为，单调递增区间为   

（2）

【解析】

【分析】（1）求导后，根据正负可得的单调区间；

（2）采用分离变量法可得，令，利用导数可求得，由此可得的范围.

【小问1详解】

当时，，，

则当时，；当时，；

的单调递减区间为，单调递增区间为.

【小问2详解】

由得：，

当时，，，

令，则；

令，则，

，在上单调递减，，

，即实数的取值范围为.

22. 已知函数.

（1）讨论的单调性.

（2）若存在两个零点，且曲线在和处的切线交于点.

①求实数的取值范围；

②证明：.

【答案】（1）答案见解析   

（2）①；②证明见解析

【解析】

【分析】（1）利用导数分成，两种情况讨论函数的单调性；

（2）①利用导数得出函数的单调性，结合函数图像得出实数的取值范围；

②由曲线在和处的切线方程联立，得出，又存在两个零点，代入得出，

要证，只需证，即证，只要证即可.

【小问1详解】

.

当时，在上单调递减；

当时，令，得.

当时，，当时，，.

所以在上单调递增，在上单调递减.

【小问2详解】

①由（1）知，当时，在上单调递减，不可能有两个零点，

当时，在上单调递增，在上单调递减，

所以，所以，

又，；，；

所以的取值范围是.

②曲线在和处的切线分别是，

联立两条切线方程得，所以.

因为所以.

要证，只需证，

即证，只要证.

令，.

则，所以在上单调递减，

所以，

所以，所以.

【点睛】已知函数零点个数求参数范围问题方法点睛：

可以通过构造函数，分情况讨论函数的单调性，结合零点存在性定理，根据零点个数，考虑图像的交点情况，得出参数的取值范围.