





2024版高考数学一轮复习教材基础练第八章平面解析几何第六节抛物线教学课件
展开知识点104:抛物线的定义及标准方程、抛物线的几何性质
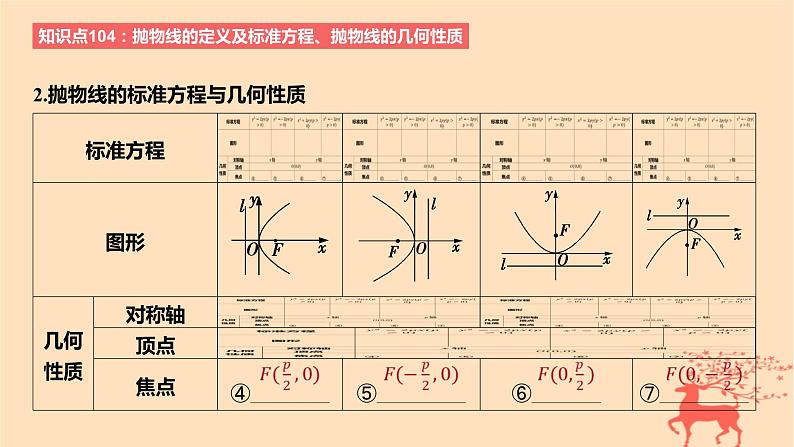
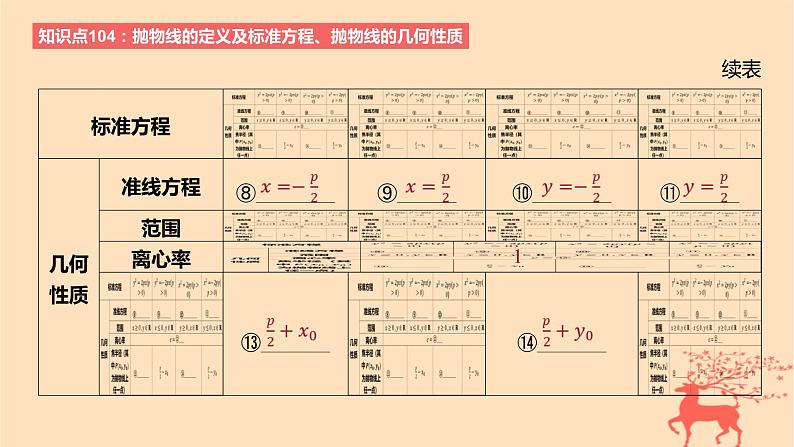
2.抛物线的标准方程与几何性质
1.利用抛物线的定义可解决的常见问题
(1)轨迹问题:利用抛物线的定义可以确定与定点、定直线距离有关的动点轨迹是否为抛物线.
(2)距离问题:涉及抛物线上的点到焦点的距离和到准线的距离问题时,在解题过程中注意两者之间的相互转化.
2.与抛物线定义有关的最值问题的两个转化策略
(1)将抛物线上的点到准线的距离转化为该点到焦点的距离,构造出“两点之间线段最短”使问题得以解决.
(2)将抛物线上的点到焦点的距离转化为该点到准线的距离,利用“直线外一点与该直线上所有点的连线中,垂线段最短”原理解决.
方法技巧抛物线的标准方程的求法
1. 若点P到点(0,2)的距离比它到直线y=-1的距离大1,则点P的轨迹方程为A.y2=4xB.x2=4yC.y2=8xD.x2=8y
2. 知A为抛物线C:y2=2px(p>0)上一点,点A到C的焦点的距离为12,到y轴的距离为9,则p=A.2B.3C.6D.9
7. [多选]设抛物线C:y2=8x的焦点为F,准线为l,点M为C上一动点,E(3,1)为定点,则下列结论正确的是A.准线l的方程是x=-2B.|ME|-|MF|的最大值为2C.|ME|+|MF|的最小值为7D.以线段MF为直径的圆与y轴相切
(1)过抛物线y2=2px(p>0)的焦点F的直线与抛物线交于A,B两点,则以AB为直径的圆与准线相切;以AF和BF为直径的圆均与y轴相切.(2)求平面上动点P到两定点A,B的距离之和的最小值时,利用|PA|+|PB|≥|AB|,当点P在线段AB上时等号成立求解,即当点P在线段AB上时,点P到两定点A,B的距离之和最小,且最小值为|AB|.(3)求平面上动点P到两定点A,B的距离之差的最大值和最小值时,利用||PA|-|PB||≤|AB|,即-|AB|≤|PA|-|PB|≤|AB|,当点P在BA的延长线上时,左边等号成立,当点P在AB的延长线上时,右边等号成立求解,即当点P在BA的延长线上时,|PA|-|PB|取得最小值,且最小值为-|AB|;当点P在AB的延长线上时,|PA|-|PB|取得最大值,且最大值为|AB|.
9. 已知抛物线x2=4y的焦点为F,定点A(1,4),点P是抛物线上一个动点,则|PF|+|PA|的最小值为A.3B.4C.5D.8
变式2 已知以圆C:(x-1)2+y2=4的圆心为焦点的抛物线C1与圆C在第一象限交于A点.过抛物线C2:x2=8y上任意一点B作直线y=-2的垂线,垂足为M,则|BM|-|AB|的最大值为A.8B.2C.-1D.1
11.已知O为坐标原点,抛物线C:y2=2px(p>0)的焦点为F,P为C上一点,PF与x轴垂直,Q为x轴上一点,且PQ⊥OP.若|FQ|=6,则C的准线方程为 .
知识点105:直线与抛物线的位置关系
解决直线与抛物线位置关系的常用技巧
1.直线与抛物线的位置关系问题的求解方法可类比直线与椭圆、双曲线的位置关系的求解方法,一般用到根与系数的关系.
2.涉及抛物线的弦长、中点、距离问题时,要注意“设而不求”“整体代入”“点差法”以及定义的灵活应用.
直线与抛物线相切的有关结论(1)抛物线y2=2px(p>0)上任意一点P(x0,y0)处的切线方程是y0y=p(x+x0);(2)过抛物线y2=2px(p>0)外一点P(x0,y0)所引两条切线的切点弦所在直线的方程是y0y=p(x+x0);(3)抛物线y2=2px(p>0)与直线Ax+By+C=0相切的条件是pB2=2AC.
6. 已知点M(-1,1)和抛物线C:y2=4x,过C的焦点且斜率为k的直线与C交于A,B两点.若∠AMB=90°,则k= .
2024版高考数学一轮复习教材基础练第八章平面解析几何数学模型6圆锥曲线的光学性质的应用教学课件: 这是一份2024版高考数学一轮复习教材基础练第八章平面解析几何数学模型6圆锥曲线的光学性质的应用教学课件,共12页。PPT课件主要包含了模型解读,应用专练等内容,欢迎下载使用。
2024版高考数学一轮复习教材基础练第八章平面解析几何结论应用4与抛物线的焦点弦有关的二级结论教学课件: 这是一份2024版高考数学一轮复习教材基础练第八章平面解析几何结论应用4与抛物线的焦点弦有关的二级结论教学课件,共18页。PPT课件主要包含了结论应用,二级结论,应用专练等内容,欢迎下载使用。
2024版高考数学一轮复习教材基础练第八章平面解析几何结论应用3与椭圆双曲线有关的二级结论教学课件: 这是一份2024版高考数学一轮复习教材基础练第八章平面解析几何结论应用3与椭圆双曲线有关的二级结论教学课件,共13页。PPT课件主要包含了结论应用,二级结论,双曲线的焦点三角形,应用专练等内容,欢迎下载使用。












