2022-2023学年广东省珠海市斗门重点中学高一（下）期中数学试卷

2022-2023学年广东省珠海市斗门重点中学高一（下）期中数学试卷

一、单选题（本大题共8小题，共40.0分。在每小题列出的选项中，选出符合题目的一项）

1.  在复平面内，复数对应的点的坐标是，则(    )

A.  B.  C.  D.

2.  已知，则的值为(    )

A.  B.  C.  D.

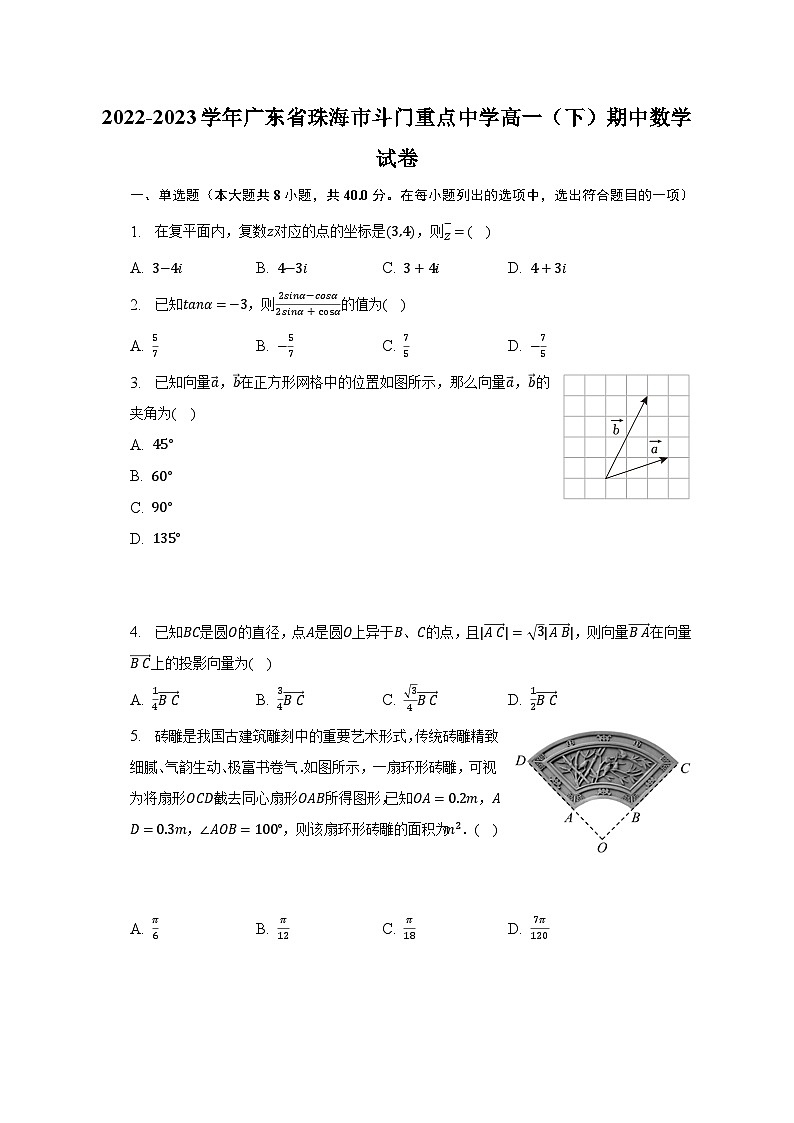
3.  已知向量，在正方形网格中的位置如图所示，那么向量，的夹角为(    )

A.
B.
C.
D.

4.  已知是圆的直径，点是圆上异于、的点，且，则向量在向量上的投影向量为(    )

A.  B.  C.  D.

5.  砖雕是我国古建筑雕刻中的重要艺术形式，传统砖雕精致细腻、气韵生动、极富书卷气．如图所示，一扇环形砖雕，可视为将扇形截去同心扇形所得图形，已知，，，则该扇环形砖雕的面积为．(    )

A.  B.  C.  D.

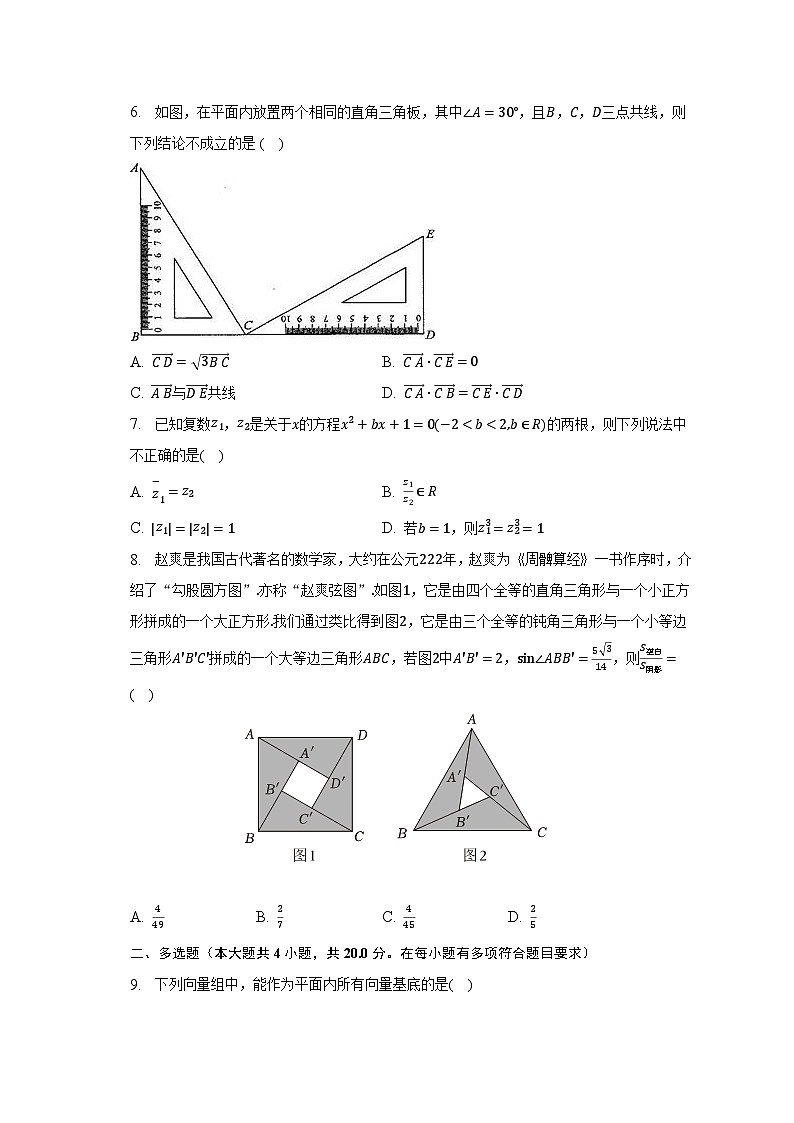
6.  如图，在平面内放置两个相同的直角三角板，其中，且，，三点共线，则下列结论不成立的是(    )
 

A.  B.
C. 与共线 D.

7.  已知复数，是关于的方程的两根，则下列说法中不正确的是(    )

A.  B.
C.  D. 若，则

8.  赵爽是我国古代著名的数学家，大约在公元年，赵爽为周髀算经一书作序时，介绍了“勾股圆方图”亦称“赵爽弦图”如图，它是由四个全等的直角三角形与一个小正方形拼成的一个大正方形我们通过类比得到图，它是由三个全等的钝角三角形与一个小等边三角形拼成的一个大等边三角形，若图中，，则(    )

A.  B.  C.  D.

二、多选题（本大题共4小题，共20.0分。在每小题有多项符合题目要求）

9.  下列向量组中，能作为平面内所有向量基底的是(    )

A. ， B. ，
C. ， D. ，

10.  如图，，是单位圆上的两个点，点的坐标为，，点以的角速度、点以的角速度均按逆时针方向开始在单位圆上运动，则(    )

A. 时，的弧度数为
B. 时，扇形的弧长为
C. 时，扇形的面积为
D. 时，点，点在单位圆上第一次重合
 

11.  已知曲线：，曲线，曲线的部分图象如图所示，则下列结论正确的是(    )

A. 将曲线的图象先向右平移个单位长度，再将图象上各点的横坐标伸长为原来的倍得到曲线的图象
B. 将曲线的图象先向右平移个单位长度，再将图象上各点的横坐标缩短为原来的倍得到曲线的图象
C. 将曲线各点的横坐标先伸长为原来的倍，再将图象向右平移个单位长度得到曲线的图象
D. 将曲线各点的横坐标先缩短为原来的倍，再将图象向右平移个单位长度得到曲线的图象

12.  欧拉公式其中是自然对数的底数，为虚数单位是由瑞士著名数学家欧拉创立，该公式将指数函数的定义域扩大到复数集，建立了三角函数与指数函数的关联，在复变函数论里面占有非常重要的地位，被誉为数学中的天桥依据欧拉公式，下列选项中正确的是(    )

A. 的模为 B. 的共轭复数为
C. 对应的点在第一象限 D. 复数的虚部为

三、填空题（本大题共4小题，共20.0分）

13.  已知向量，，若，则 ______ ．

14.  一游客在处望见在北偏东的方向上有一塔，在南偏东的方向上有一塔，测得、间的距离为公里，，两点间的距离为公里，则塔与塔间的距离为______ 公里．

15.  复数与复数在复平面内对应的点分别是，，为坐标原点，则 ______ ．

16.  设，则 ______ ．

四、解答题（本大题共6小题，共70.0分。解答应写出文字说明，证明过程或演算步骤）

17.  本小题分
已知复数是纯虚数为虚数单位，为实数．
求的值；
若复数在复平面内对应的点在第四象限，求实数的取值范围．

18.  本小题分
某同学用“五点法”画函数在某一个周期内的图象时，列表并填入了部分数据，如下表：

请将上表数据补充完整，并直接写出函数的解析式；
将图象上所有点向左平移个单位长度，得到的图象若图象的一个对称中心为，求的最小值．

19.  本小题分
在中，，，的对边分别为，，，且满足．
求；
若，求的取值范围．

20.  本小题分
已知向量，，函数．
求的最小正周期；
求的单调增区间，对称轴；
求在区间上的最大值和最小值以及对应的的值．

21.  本小题分
已知，，，．
求的值；
求的值．

22.  本小题分
已知向量，，且，且，．
若与夹角，求；
记，是否存在实数，使，对任意恒成立，若存在，求出实数的取值范围；若不存在，请说明理由．

答案和解析

1.【答案】 

【解析】解：复数对应的点的坐标是，
则，
故．
故选：．
根据已知条件，结合复数的几何意义，以及共轭复数的定义，即可求解．
本题主要考查共轭复数的定义，以及复数的几何意义，属于基础题．
 

2.【答案】 

【解析】解：因为，
所以．
故选：．
由已知利用同角三角函数基本关系式即可求解．
本题考查了同角三角函数基本关系式在三角函数化简求值中的应用，属于基础题．
 

3.【答案】 

【解析】解：根据题意，如图，建立坐标系，设小正方形的边长为，向量，的夹角为，
则，，
则，，，
则，
则，
故选：．
根据题意，建立坐标系，求出、的坐标，即可得、以及的值，由向量夹角公式可得的值，结合的范围分析可得答案．
本题考查向量数量积的计算，涉及向量的坐标计算，属于基础题．
 

4.【答案】 

【解析】解：设，
则，
是圆的直径，点是圆上异于、的点，
由圆的性质可知，，
，
，
为的内角，
，
向量在向量上的投影向量为：．
故选：．
根据已知条件，结合圆的性质，以及投影向量的公式，即可求解．
本题主要考查投影向量的公式，属于基础题．
 

5.【答案】 

【解析】解：由题意得该扇环形砖雕的面积．
故选：．
由已知结合扇形的面积公式即可求解．
本题主要考查了扇形面积公式的应用，属于基础题．
 

6.【答案】 

【解析】

【分析】
本题考查了直角三角形的性质，向量线性运算，属于中档题．
根据直角三角形的性质、向量的线性运算，即可判定．
【解答】
解：设，，且，，三点共线，
则，，
，，
，，故A、、成立；
故选：．  

7.【答案】 

【解析】解：，，
不妨设，，
，故A正确；
，故C正确；
，，时，，故B错误；
时，，
，
，，同理，故D正确．
故选：．
在复数范围内解方程得，，然后根据复数的概念、运算判断各选项．
本题考查复数的运算法则等基础知识，考查运算求解能力，是基础题．
 

8.【答案】 

【解析】解：，且，，
在中，设，则，由题知，，
，
由正弦定理：，即，，
由余弦定理：，
，
，，
，
．
故选：．
设，根据题意知，利用同角三角函数的基本关系和正、余弦定理即可求出，，再由面积公式即可求得．
本题考查了解三角形的应用问题，也考查了运算求解能力，属于中档题．
 

9.【答案】 

【解析】解：两向量不共线，则能作为平面内所有向量的一组基底．
选项，，与不共线；
选项，，与不共线；
选项，，与不共线；
选项，，与共线，
综上，，，中两个向量能作为基底，
故选：．
由基底定义，需判断选项中两个向量是否共线，由向量共线的坐标关系即可判断．
本题考查基底的概念，向量共线的坐标关系，属基础题．
 

10.【答案】 

【解析】解：时，点按逆时针方向运动，点按逆时针方向运动，此时的弧度数为，故A不正确；
时，的弧度数为，故扇形的弧长为，故B正确；
时，的弧度数为，故扇形的面积为，故C正确；
设时，点，点在单位圆上第一次重合，则，解得，故D不正确．
故选：．
根据已知条件，结合弧长公式及扇形面积公式，逐项分析即可求解．
本题主要考查了弧长公式及扇形面积公式的应用，属于基础题．
 

11.【答案】 

【解析】解：因为图象过，故，而，故．
又图象在轴右侧的第一个对称中心为，故，即，
因此，曲线，
选项，将向右平移个单位，得到函数图象，再将横坐标伸长为原来的倍，则可得的图象，故正确；
选项，将向右平移个单位，得到函数图象，再将横坐标缩短为原来的倍，则可得的图象，故错误；
选项，将各点的横坐标伸长为原来的倍，得到函数的图象，再将图象向右平移个单位，则可得的图象，故正确；
选项，将各点的横坐标先缩短为原来的倍，得到函数的图象，再将图象向右平移个单位，则可得的图象，故错误．
故选：．
先求对应的函数解析式，从而可得两者之间的变化过程．
本题考查了由图象求解析式以及三角函数的图象变换规律，属简单题．
 

12.【答案】 

【解析】解：对于，，其模为，故A正确；
对于，，其共轭复数为，故B正确；
对于，，对应的点在第一象限，故C正确；
对于，
，
所以虚部为，故D错误．
故选：．
根据已知条件，结合欧拉公式，以及复数的性质，即可求解．
本题主要考查欧拉公式的应用，属于中档题．
 

13.【答案】 

【解析】解：根据题意，向量，，
若，则，解可得；
故答案为：．
根据题意，由向量数量积的计算公式可得，解可得的值，即可得答案．
本题考查向量垂直的判断，涉及向量数量积的坐标计算，属于基础题．
 

14.【答案】 

【解析】解：依题意可得，，，

由余弦定理，
即，所以，即塔与塔间的距离为公里．
故答案为：．
利用余弦定理计算可得．
本题考查了余弦定理的应用计算，属于中档题．
 

15.【答案】 

【解析】解：，，
复数与复数在复平面内对应的点分别是，，
则，，
设，，
则，，
故，
故．
故答案为：．
根据已知条件，先求出点，的坐标，再结合正切函数的两角和公式，即可求解．
本题主要考查复数的四则运算，以及复数的几何意义，属于基础题．
 

16.【答案】 

【解析】解：，



，
设，
则，
，．
故答案为：．
根据题意可得，从而易得，再根据倒序相加法，即可求解．
本题考查三角恒等变换，函数的对称性质，利用倒序相加法求和，化归转化思想，属中档题．
 

17.【答案】解：复数是纯虚数，
则，解得；
由可知，，
故复数，
复数在复平面内对应的点在第四象限，
，解得，
故实数的取值范围为； 

【解析】根据已知条件，结合纯虚数的定义，即可求解；
根据已知条件，结合复数的四则运算，以及复数的几何意义，即可求解．
本题主要考查复数的四则运算，以及复数的几何意义，属于基础题．
 

18.【答案】解：依题可得，，，所以函数，

将图象上所有点向左平行移动个单位长度，
得到，又图象的一个对称中心为，
所以，所以，，又，
所以，且，所以时取到最小值是． 

【解析】根据五点法，计算即可填表，写出解析式；先写出的解析式，用代入法求出的最小值．
本题考查三角函数图象的性质，五点法，属于基础题．
 

19.【答案】解：在中，，，的对边分别为，，，且满足，
由正弦定理得，，
，，
，
，
，，
，又，
；
由正弦定理得，，
所以，，，
所以，
故的取值范围为 

【解析】利用正弦定理和三角公式得到，即可求出；
利用正弦定理表示出，，利用三角函数求出最值．
本题主要考查了余弦定理，正弦定理，和差角公式在求解三角形中的应用，属于中档题．
 

20.【答案】解：，
，
的最小正周期为；
令，
，
的单调增区间为，，
令，，，
的对称轴为；
，，
当，即时，有最大值；
当，即时，有最小值，
当时，，当时，． 

【解析】用向量的数量积和三角恒等变换知识将化为即可得到答案；
解不等式和方程即可；
由复合函数的值域及正弦函数的值域即可求出．
本题考查三角恒等变换和三角函数的性质，考查了函数对基础知识的掌握，属于中档题．
 

21.【答案】解：，
，
又，，
，

；
由知，又，
，
，，
，又，
，


． 

【解析】根据及诱导公式与同角关系．即可求解；
根据及同角关系，即可求解．
本题考查三角函数求值问题，三角函数公式的应用，化归转化思想，属中档题．
 

22.【答案】解：因为，
所以，
又，与夹角，
即，
即，
即，
即；
由可得，
即，
设存在实数，使，对任意恒成立，
即对恒成立，
即对恒成立，
设，，
由已知可得对恒成立，
即，
即，
即，
即存在实数，使，对任意恒成立，且实数的取值范围为． 

【解析】由平面向量的模的运算，结合平面向量数量积的运算求解即可；
由可得，设存在实数，使，对任意恒成立，对恒成立，设，，即对恒成立，即，然后求解即可．
本题考查了平面向量数量积的运算，重点考查了不等式恒成立问题，属基础题．