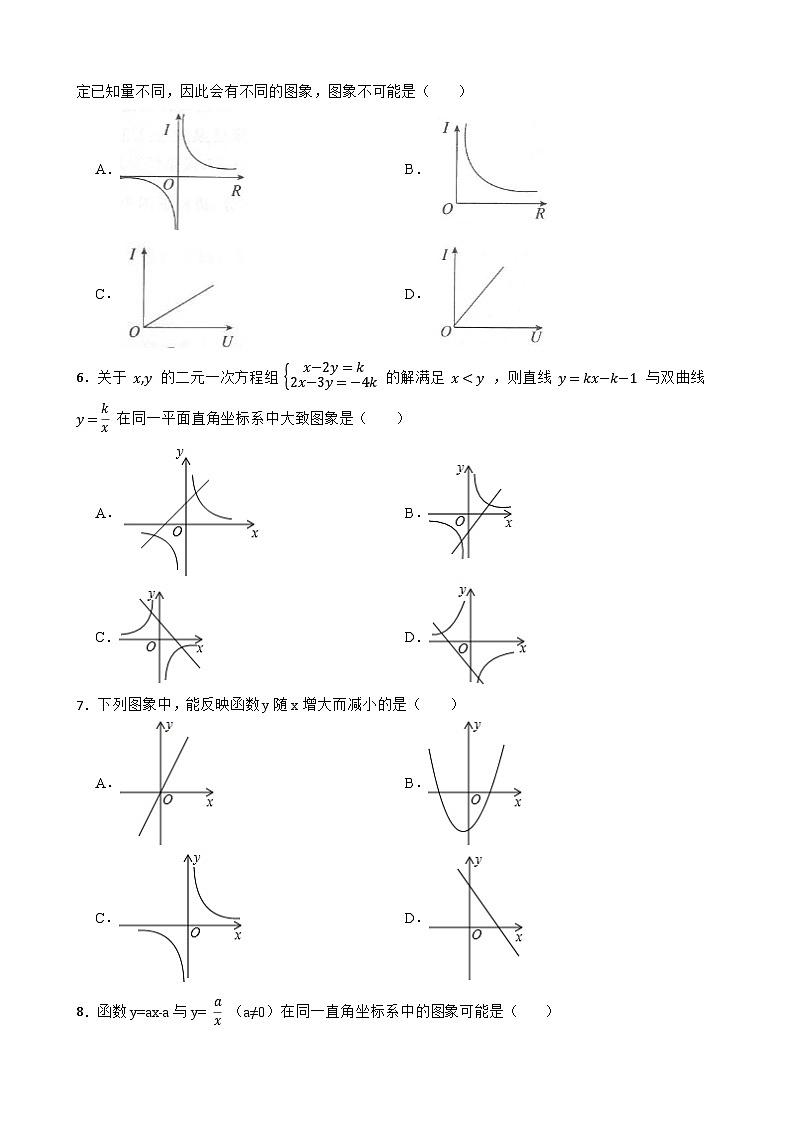
人教版数学九年级下册第二十六章、反比例函数 试卷

这是一份人教版数学九年级下册第二十六章、反比例函数，共26页。

初中数学试卷
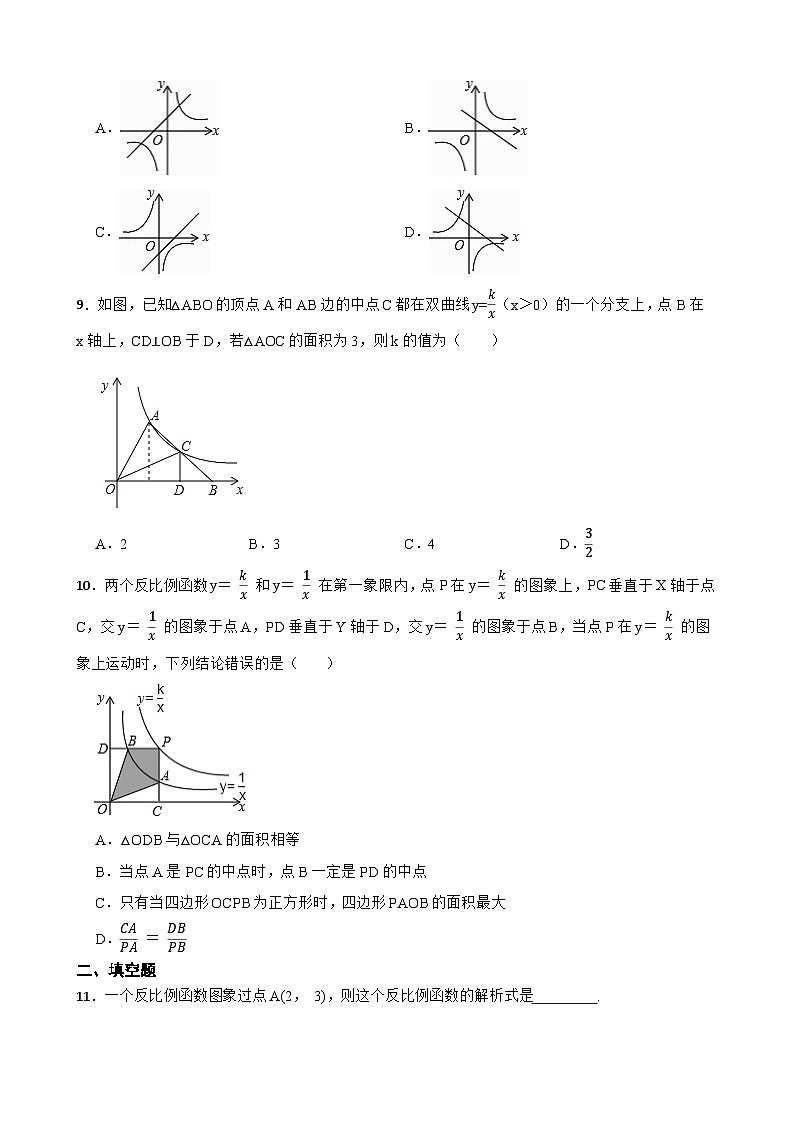
一、单选题
1．已知函数：(1)xy=9；(2)y= 6x ；(3)y=- 23x ；(4)y= 2x2 ；(5) y= 3x−1 ，其中反比例函数的个数为(　　)
A．1 B．2 C．3 D．4
2．已知一次函数 y1=x−1 与反比例函数 y2=2x 的图象交于点 A(2，1)，B(−1，−2) ，则 y1>y2 时 x 的取值范围为（　　）

A．x>2 B．x>2 或 −10, 可知反比例函数图象经过一、三象限。
13．【答案】t=38v
【知识点】列反比例函数关系式
【解析】【解答】解：∵路程为38，速度为v，
∴时间t=38v，
故答案为：t=38v．
【分析】路程=速度÷时间，把相关数值代入即可求解．
14．【答案】5⩽x⩽252
【知识点】反比例函数与一次函数的交点问题
【解析】【解答】解：把x＝1和x＝4分别代入y＝ 2x 得，y＝2和y＝ 12 ，
把当x＝1，y＝2和当x＝4，y＝ 12 代入y＝﹣3x+b得到b＝5和b＝ 252
所以直线y＝﹣3x+b与双曲线y＝ 2x 在1≤x≤4范围内有公共点，则b的取值范围是：5≤x≤ 252 ，
故答案为 5⩽x⩽252 ．
【分析】分别将x=1、x＝4代入y＝ 2x中，求出y值，然后将x＝1，y＝2和当x＝4，y＝ 12 代入y＝﹣3x+b中，分别求出b值，由两图象在1≤x≤4范围内有公共点，从而可得b的范围.
15．【答案】8
【知识点】反比例函数系数k的几何意义；中心对称及中心对称图形
【解析】【解答】解：过点B作BC⊥y轴于点C，过点A作AD⊥y轴于点D,

∴∠BCP=∠ADP=90°，
∵ 点A与点B关于P成中心对称
∴BP=AP，
在△BPC和△APD中
∠BCP=∠ADP∠BPC=∠APDBP=AP
∴△BPC≌△APD（AAS）
∴S△BPC=S△APD，
∴S△AOB=S△BPO+S△AOD+S△ADP=S△BPO+S△BCP+S△AOD=S△BCO+S△AOD，
∵点A、B分别在反比例函数y= k1x (k1＞0) 和 y= k2x (k2＜0)的图象上，
∴S△BCO+S△AOD=12k2+12k1=12k1−k2=4,
∴ k1-k2= 8.
故答案为：8.
【分析】过点B作BC⊥y轴于点C，过点A作AD⊥y轴于点D，利用中心对称的性质，可知BP=AP，再利用AAS证明△BPC≌△APD，利用两全等三角形的面积相等，可证得S△BPC=S△APD，再证明S△AOB=S△BCO+S△AOD=4，然后利用函数解析式，可得到S△BCO+S△AOD与k1，k2的关系，从而可求出k1-k2的值。
16．【答案】-2
【知识点】反比例函数系数k的几何意义；平行线的性质
【解析】【解答】解：∵直线AB∥x轴，
∴AC⊥y轴，BC⊥y轴，
∴S△AOC= 12 |k|，S△BOC= 12 ×4=2，
∵S△AOB=3，
∴S△AOC=1，
∴|k|=2，
∵k＜0，
∴k=-2，
故答案为：-2．

【分析】根据反比例函数中系数k的几何意义，结合平行线的性质以及撒娇行的面积公式，求出答案即可。
17．【答案】(6,2）
【知识点】待定系数法求反比例函数解析式；矩形的性质；反比例函数图象上点的坐标特征
【解析】【解答】 ∵ 点 A 的坐标为 (3,4) ， AB=2 ，
∴B(3,2) ，
∵ 四边形 ABCD 是矩形，
∴AD//BC ，
∵AD//x 轴，
∴BC//x 轴，
∴C 点的纵坐标为2，
设 C(x,2) ，
∵ 矩形 ABCD 的顶点 A ， C 在反比例函数 y=kx(k>0,x>0) 的图象上，
∴k=2x=3×4 ，
∴x=6 ，
∴C(6,2) ，
故答案为 (6,2) .
【分析】根据矩形的性质和 A 点的坐标，即可得出 C 的纵坐标为2，设 C(x,2) ，根据反比例函数图象上点的坐标特征得出 k=2x=3×4 ，解得 x=6 ，从而得出 C 的坐标为 (6,2) .
18．【答案】7
【知识点】反比例函数系数k的几何意义；三角形全等的判定（AAS）
【解析】【解答】解：延长CD，EF交于H，延长DA交x轴于G，延长AB交EF于N，

则△DHF≌△AGE≌△AEN，
∴S四边形ABOE=S四边形ADHE，
∴S四边形ABOG=S四边形AEFD=7，
∵双曲线y=kx过点A，
∴k=7.
故答案为：7.
【分析】延长CD、EF交于H，延长DA交x轴于G，延长AB交EF于N，则△DHF≌△AGE≌△AEN，结合面积间的和差关系可得S四边形ABOG=S四边形AEFD=7，然后根据反比例函数系数k的几何意义进行解答.
19．【答案】9
【知识点】反比例函数系数k的几何意义
【解析】【解答】解：过A作AH⊥BO于H，AE⊥x轴于E，过C作CD⊥x轴于D，

∵点A是反比例函数y= kx （x＞0）的图象上一点，
∴S△AHO=S△AOE= 12 k，
∵AB=AO，
∴BH=OH，
∴S△ABH=S△AOH= 12 k，
∴S△AOB=k，
∵点C反比例函数y= 1x （x＞0）的图象上，
∴S△COD= 12 ，
∵CD∥AE，
∴△COD∽△AOE，
∴S△CODS△AOE =（ OCAO ）2= 1k ，
∴OCOA = 1k ，
∴S△BOCS△AOB = 1k ，
∵△ABC的面积为6，
∴1k = k−6k ，
解得k=9，k=4（不合题意，舍去），
∴k=9．
故答案为：9．
【分析】出现等腰三角形时常用辅助线是过顶角顶点作底边的高，得出中线，利用相似三角形的性质，面积比等于相似比的平方，数形结合，求k可转化为求S△AOB，构建关于k的方程，求出k.
20．【答案】6
【知识点】反比例函数的图象；反比例函数系数k的几何意义
【解析】【解答】解：∵△OAB和△BCD都是等腰直角三角形，
∴OA＝AB，CD＝BD．
设OA＝a，CD＝b，则点C的坐标为（a+b，a﹣b），
∵反比例函数y＝ kx 的图象经过点C，
∴（a+b）（a﹣b）＝a2﹣b2＝k，
∴△OAB与△BCD的面积之差＝ 12 a2﹣ 12 b2＝ 12 k＝3，
∴k＝6，
故答案为6．

【分析】根据△OAB和△BCD都是等腰直角三角形，可得OA=AB，CD=BD．设OA=a，CD=b，则点C的坐标为（a+b，a-b），根据反比例函数y＝ kx 的图象经过点C，即可得到a2-b2=k，进而得出△OAB与△BCD的面积之差 =12a2−12b2=12k=3 ，解得即可．
21．【答案】解：∵y=(m+2)xm2+3m+1是关于x的反比例函数，
∴m2+3m+1=−1m+2≠0.，
解得m=−1或m=−2m≠−2，
∴m=−1，
故答案为：-1.
【知识点】反比例函数的定义
【解析】【分析】由反比例函数的定义 y=kx−1，自变量的指数必须是-1，同时k≠0，即可列出 m2+3m+1=−1m+2≠0.求解 .
22．【答案】（1）解：把B（2，n）代入y=2x得：n=2×2=4，
∴B点坐标为（2，4）；
（2）解：设过B点的反比例函数解析式为y= kx ，
把B（2，4）代入有4= k2 ，k=8．
∴所求的反比例函数解析式为y= 8x ．
【知识点】反比例函数与一次函数的交点问题
【解析】【分析】（1）把B（2，n）代入正比例函数y=2x即可求出n的值，进而可求出B点坐标；（2）把B（2，n）代入反比例函数 y=3x 求出k的值，即可求出这个反比例函数的解析式．
23．【答案】解：设 y1=k1x2 ， y=k2x+3 则 y=k1x2+k2x+3,k23=2k1+k24=0 解得 k1=32k2=6 ， ∴y=32x2+6x+3 当x=3时，y的值为 −252
【知识点】反比例函数的定义；正比例函数的定义
【解析】【分析】先根据反比例函数和正比例函数的定义分别设y1和y2的函数式，再分别代入 中得到y的函数式，现知图象过两个定点，利用待定系数法即可求出y的函数式，把x=3代入函数式即可求出这时的y值.
24．【答案】（1）解：把x＝1，y＝3代入y＝ Kx 得：3＝ k1 ，
解得：k＝3
（2）解： tt−1−1=3t2−1 ，
去分母得：t（t+1）﹣（t2﹣1）＝3，
t2+t﹣t2+1＝3，
t＝2，
检验：把t＝2代入最简公分母t2﹣1≠0，
∴原分式方程的解为t＝2，
因此：k＝3，t＝2
【知识点】解分式方程；待定系数法求反比例函数解析式
【解析】【分析】（1）由题意把x＝1，y＝3，代入反比例函数y＝ kx ，即可求k值；（2）根据题意把k的值代入分式方程解方程可得t的值.
25．【答案】（1）解：把 P(−2，a) 代入直线 y=−2x 解析式得： a=4 ，即 P(−2，4) ，
∴点P关于y轴对称点 P′ 为 (2，4) ，代入反比例解析式得： k=8 ，
则反比例解析式为 y=8x ；
（2）解：当 y−2 ．
【知识点】待定系数法求反比例函数解析式；反比例函数与一次函数的交点问题
【解析】【分析】（1）把P（-2，a）代入直线y=-2x解析式得：a=4，即P（-2，4），再求出点P关于y轴的对称点，代入计算即可；（2）根据图象，利用函数值大的图象在上方的原则直接写出答案。
26．【答案】（1）∵双曲线 y=mx 过 A(3,−2) ，将 A(3,−2) 代入 y=mx ，解得： m=−6 ．
∴所求反比例函数表达式为： y=−6x ．
∵点 A(3,−2) ，点 B(0,1) 在直线 y=kx+b 上，∴−2=3k+b ， b=1 ，∴k=−1 ，∴所求一次函数表达式为 y=−x+1 ．
（2）由 A(3,−2) ， B(0,1) 可得： AB=32+(1+2)2=32 ，∴BC=32 ．
又∵BO=1 ，∴CO=32+1 或 32−1 ，∴C(0 ， 32+1 ) 或 C(0 ， 1−32 ) ．
【知识点】一次函数的图象；一次函数图象与坐标轴交点问题；反比例函数图象上点的坐标特征；平面直角坐标系的构成
【解析】【分析】（1）一次函数 y=kx+b 过 A(3,−2) ， B(0,1) ，将其两点代入解析式，即可求解得到k,b的值，从而写出函数表达式。反比例函数 过 A(3,−2) ，将其代入即可得m的值，故求出函数表达式。
（2）根据坐标利用勾股定理即可求出BA的长度，点C有两种情况，即在坐标轴原点以上或以下 。然后即可求出点C的坐标。
27．【答案】解：∵y=（m﹣2）x 3−m2 是反比例函数，
∴3﹣m2=﹣1，m﹣2≠0，
解得：m=﹣2．
故m的值为﹣2．
【知识点】反比例函数的定义
【解析】【分析】判断一个函数是否是反比例函数，首先看看两个变量是否具有反比例关系，然后根据反比例函数的定义去判断．
28．【答案】（1）解：原式=1+9 3 +（1- 19 ×18）
=1+9 3 -1=9 3
（2）解：由已知可得：
y=2xy=2x ，
解之可得： x=1y=2 或 x=−1y=−2 ，
∵原式= (x+y)(x−y)(x−y)2⋅(x−y)(2x+3y)x+y−2y−3x
= 2x+3y−2y−3x
=y-x，
∴当 x=1y=2 时，原式=2-1=1；
当 x=−1y=−2 时，原式=-2-（-1）=-1；
∴原式的值为1或-1．
【知识点】实数的运算；反比例函数与一次函数的交点问题
【解析】【分析】（1）先利用0指数幂、二次根式的性质和负指数幂的性质化简，再计算即可；
（2）先利用分式的混合运算化简，再求出两函数的交点坐标，最后计算即可。
29．【答案】（1）解：设点P (x, y)，则MP=y，由OA的中点为M知O4= 2x，代入OA.MP=12,
得2x.y=12，即xy=6.
∴k= xy=6.
（2）解：当t=1时，令y=0， 0=−12(x−1)(x+3),∴x1=1,x2=−3
∴由B在A左边，得B (-3，0)，A (1, 0)，∴AB=4.
∵L的对称轴为x=-1，而M为( 12 ，0),
∴MP与L对称轴的距离为 32 .
（3）解：∵A (t, 0)，B (t-4，0),
∴L的对称轴为x=t-2.
又MP为x= t2
当t-2≤ t2 ,即t≤4时，顶点(t-2，2)就是G的最高点;
当t>4时，L与MP的交点( t2 , −18t2+t )就是G的最高点.
（4）解：5≤t≤8- 2 或7≤1≤8+ 2
【知识点】反比例函数图象上点的坐标特征；二次函数图象上点的坐标特征；二次函数y=ax^2+bx+c的图象；二次函数y=ax^2+bx+c的性质
【解析】【分析】这道题小问多，最后两道有点难度，但是只要想到就不难，尤其是最后一问，两种情况，可能由于图的影响，少考虑一种。第一问利用OA·MP=12，可以轻松求解；对称轴x=（x1+x2）/2,有t的值就可以求了；第三问是二次函数最高点的比较，增减情况，随t值变化；第四问列不等式方程，根据图求就可以了。
30．【答案】（1）B ( 3 ， 3 )；
（2）设点 P ( m ， m2+2m ).
当四边形 PEOF 是正方形时， PE=PF ，
当点 P 在第二象限时，有 m2+2m=−m .
解得 m1=0 ， m2=−3 .
∵m≠0 ，
∴m=−3 .
∴正方形 PEOF 的边长为 3 .
（3）设点 P ( m ， m2+2m )，则点E（ m ， 0 ），则点F( 0 ， m2+2m ).
∵E 为抛物线顶点，
∴该抛物线解析式为 y=a(x−m)2 .
∵抛物线经过点 F ，
∴m2+2m=a(0−m)2 ，化简得 a=2m+1 .
对于 y=x2+2x ，令 y=−1 ，解得 x1=x2=−1 ； 令 y=3 ，解得 x1=−3，x2=1 .
∵点 P 在正方形 ABCD 内部，
∴−1 ＜ m ＜ 1 ，且 m≠0 .
①当 −1 ＜ m ＜ 0 时
由反比例函数性质知 2m2 ，∴a ＞ 3 .
【知识点】反比例函数的图象；反比例函数的性质；正方形的性质；二次函数图象上点的坐标特征
【解析】【分析】（1）先由A点和D点坐标求出AD=4 ；再根据正方形的性质和A点坐标得出答案。
（2）由点P在抛物线上可设点P（m，m2+2m）， 当四边形PEOF 是正方形时，PE=PF，再由P点在第二象限 可得P点的纵横坐标互为相反数；据此列方程求出m即可得到正方形PEOF的边长；
（3）设P（m，m2+2m）（m≠0），则点E（m，0），F（0，m2+2m）， 由E为抛物线顶点可得抛物线解析式为y=a（x-m）2，再把F（0，m2+2m）代入得 ；由点P 在正方形ABCD 内部，得 -1＜ m ＜ 1，且 .最后根据 反比例函数性质分①当 -1 ＜ m ＜ 0 时②当 0＜ m ＜1 时两种情况讨论即可得出答案。
31．【答案】解：由函数y=（m+3）xm²+3m+1为反比例函数可知m2+3m+1=-1，且m+1≠0
解得m=-1（舍去），m=-2，
m的值是-2
【知识点】反比例函数的定义
【解析】【分析】由于是反比例函数，所以x的次数为-1，m2+3m+1=-1.这里要注意系数不为零，舍去不合题意的解.
32．【答案】解：∵函数y=13x2m+1是反比例函数，
∴2m+1=1，
解得：m=0．
【知识点】反比例函数的定义
【解析】【分析】根据反比例函数的定义．即y=kx（k≠0），只需令2m+1=1即可．
33．【答案】解：由题意得：m2﹣2=﹣1，
解得：m=±1．
【知识点】反比例函数的定义
【解析】【分析】根据反比例函数定义可得m2﹣2=﹣1，再解即可．
34．【答案】解：在矩形OABC中，AB=OC=2，∵点F是AB的中点，∴AF= 12 AB= 12 ×2=1，又∵OA=3，∴点F的坐标为（3，1），∴k•3﹣1=1，解得k=3，所以，反比例函数解析式为y= 3x
【知识点】待定系数法求反比例函数解析式；矩形的性质；反比例函数图象上点的坐标特征
【解析】【分析】根据矩形的性质求出AB的长，点F是AB的中点，求出AF的长，根据OA的长，可得到点F的坐标，用待定系数法求出此函数解析式。
35．【答案】解：∵点B（2，n）、P（3n﹣4，1）在反比例函数y= mx （x＞0）的图象上，
∴2n=m3n−4=m ．
解得：m=8，n=4．
∴反比例函数的表达式为y= 8x ．
∵m=8，n=4，
∴点B（2，4），（8，1）．
过点P作PD⊥BC，垂足为D，并延长交AB与点P′．

在△BDP和△BDP′中，
∠PBD=∠P′BDBD=BD∠BDP=∠BDP′
∴△BDP≌△BDP′．
∴DP′=DP=6．
∴点P′（﹣4，1）．
将点P′（﹣4，1），B（2，4）代入直线的解析式得： 2k+b=4−4k+b=1 ，
解得： k=12b=3 ．
∴一次函数的表达式为y= 12 x+3
【知识点】反比例函数与一次函数的交点问题
【解析】【分析】将点B（2，n）、P（3n﹣4，1）代入反比例函数的解析式可求得m、n的值，从而求得反比例函数的解析式以及点B和点P的坐标，过点P作PD⊥BC，垂足为D，并延长交AB与点P′．接下来证明△BDP≌△BDP′，从而得到点P′的坐标，最后将点P′和点B的坐标代入一次函数的解析式即可求得一次函数的表达式．
36．【答案】解：∵直线y=﹣2x+4与坐标轴分别交于C、B两点，∴令y=0，可得﹣2x+4=0，解得x=2，即C（2，0），OC=2，令x=0，可得y=4，即B（0，4），OB=4，①如图1，当∠OBC=∠COP时，△OCP∽△BOC，∴OBOC=OCCP，即42=2CP，解得CP=1，∴P（2，﹣1），设过点P的双曲线解析式y=kx，把P点代入解得k=﹣2，∴过点P的双曲线解析式y=﹣2x，②如图2，当∠OBC=∠CPO时，△OCP∽△COB，在△OCP和△COB中，∠OBC=∠CPO∠COB=∠OCPCO=OC∴△OCP≌△COB（AAS）∴CP=BO=4，∴P（2，﹣4）设过点P的双曲线解析式y=kx，把P点代入得﹣4=k2，解得k=﹣8，∴过点P的双曲线解析式y=−8x．综上可得，过点P的双曲线的解析式为y=﹣2x​或y=−8x．
【知识点】一次函数的实际应用；待定系数法求反比例函数解析式；相似三角形的判定与性质
【解析】【分析】由直线y=﹣2x+4与坐标轴分别交于C、B两点，易得OC=2，OB=4，再分两种情况①当∠OBC=∠COP时，△OCP与△OBC相似，②当∠OBC=∠CPO时，△OCP与△OBC相似分别求出点的坐标，再求出过点P的双曲线解析式．