易错点22 不等式选讲（学生版）-备战2022年高考数学考试易错题

这是一份易错点22 不等式选讲（学生版）-备战2022年高考数学考试易错题，共6页。试卷主要包含了含绝对值不等式的解法，不等式的证明，柯西不等式的应用等内容，欢迎下载使用。
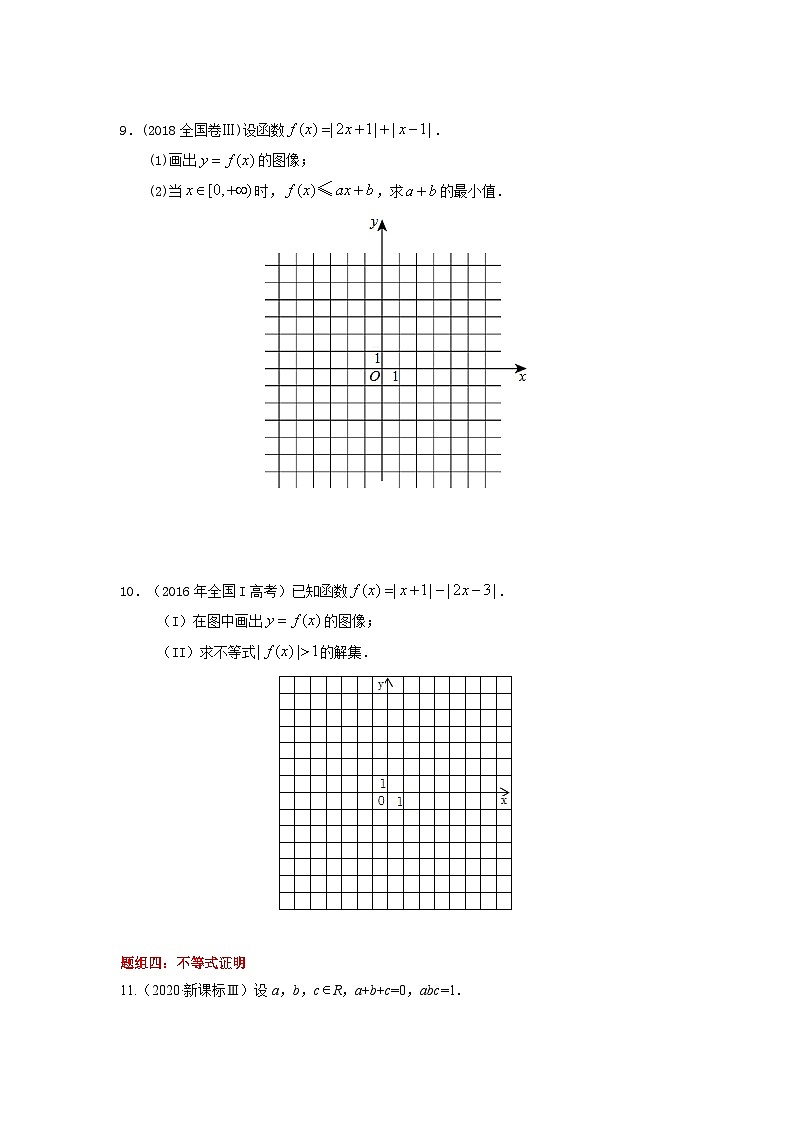
易错点22   不等式选讲易错点1、含绝对值不等式的解法(1)用零点分段法解绝对值不等式的步骤：①求零点；②划区间、去绝对值号；③分别解去掉绝对值的不等式；④取每个结果的并集，注意在分段时不要遗漏区间的端点值．(2)用图象法、数形结合可以求解含有绝对值的不等式，使得代数问题几何化，既通俗易懂，又简洁直观，是一种较好的方法．易错点2、不等式的证明(1)作差法应该是证明不等式的常用方法．作差法证明不等式的一般步骤：①作差；②分解因式；③与0比较；④结论．关键是代数式的变形能力．(2)在不等式的证明中，适当“放”“缩”是常用的推证技巧．易错点3、柯西不等式的应用(1)使用柯西不等式证明的关键是恰当变形，化为符合它的结构形式，当一个式子与柯西不等式的左边或右边具有一致形式时，就可使用柯西不等式进行证明．(2)利用柯西不等式求最值的一般结构为(a＋a＋…＋a)(＋＋…＋)≥(1＋1＋…＋1)2＝n2.在使用柯西不等式时，要注意右边为常数且应注意等号成立的条件．题组一：含绝对值不等式（一）1. 【2021年乙卷】已知函数．（1）当时，求不等式的解集;（2）若，求a的取值范围． 2.（2020·新课标Ⅱ）已知函数.（1）当时，求不等式的解集；（2）若，求a的取值范围.3. （2019全国II理23）已知 （1）当时，求不等式的解集；（2）若时，，求的取值范围. 4．(2018全国卷Ⅱ) 设函数．(1)当时，求不等式的解集；(2)若，求的取值范围． 题组二：含绝对值不等式（二）5. 【2021年甲卷】已知函数．（1）画出和的图像；（2）若，求a的取值范围． 6．(2018全国卷Ⅰ)已知．(1)当时，求不等式的解集；(2)若时不等式成立，求的取值范围．  7．（2017新课标Ⅰ）已知函数，．(1)当时，求不等式的解集；(2)若不等式的解集包含，求的取值范围． 题组三：含绝对值不等式（三）8.（2020·新课标Ⅰ）已知函数．（1）画出的图像；（2）求不等式的解集．   9．(2018全国卷Ⅲ)设函数．(1)画出的图像；(2)当时，，求的最小值．   10．（2016年全国I高考）已知函数．（I）在图中画出的图像；（II）求不等式的解集． 题组四：不等式证明11.（2020·新课标Ⅲ）设a，b，cR，a+b+c=0，abc=1．（1）证明：ab+bc+ca<0；（2）用max{a，b，c}表示a，b，c中的最大值，证明：max{a，b，c}≥． 12.（2019全国I理23）已知a，b，c为正数，且满足abc=1．证明：（1）；（2）． 13.（2019全国III理23）设，且.（1）求的最小值；（2）若成立，证明：或.  14．（2017新课标Ⅱ）已知，，，证明：(1)；(2)． 15．（2015新课标2）设均为正数，且，证明：（Ⅰ）若>，则；（Ⅱ）是 的充要条件．  1．已知函数．(1)求不等式的解集；(2)若不等式的解集非空，求的取值范围． 2．已知函数，．（Ⅰ）当时，求不等式的解集；（Ⅱ）若的图像与轴围成的三角形面积大于6，求的取值范围． 3．设函数=（Ⅰ）证明：2；（Ⅱ）若，求的取值范围．  4．已知函数=,=.（Ⅰ）当=-2时，求不等式＜的解集；（Ⅱ）设＞-1,且当∈[，)时，≤,求的取值范围. 5．已知函数．（Ⅰ）当时，求不等式的解集；（Ⅱ）若的解集包含，求的取值范围． 6．设函数,其中．（Ⅰ）当时，求不等式的解集；（Ⅱ）若不等式的解集为 ，求a的值． 7．已知函数（Ⅰ）当a=2时，求不等式的解集；（Ⅱ）设函数，当时，，求a的取值范围． 8．若，且．(Ⅰ) 求的最小值；（Ⅱ）是否存在，使得？并说明理由． 9．设均为正数，且，证明：（Ⅰ）（Ⅱ） 10．已知函数，M为不等式的解集．（I）求M；（II）证明：当a，时，．