易错点10 不等式（解析版）-备战2022年高考数学考试易错题

这是一份易错点10 不等式（解析版）-备战2022年高考数学考试易错题，共12页。试卷主要包含了已知函数，，已知函数等内容，欢迎下载使用。
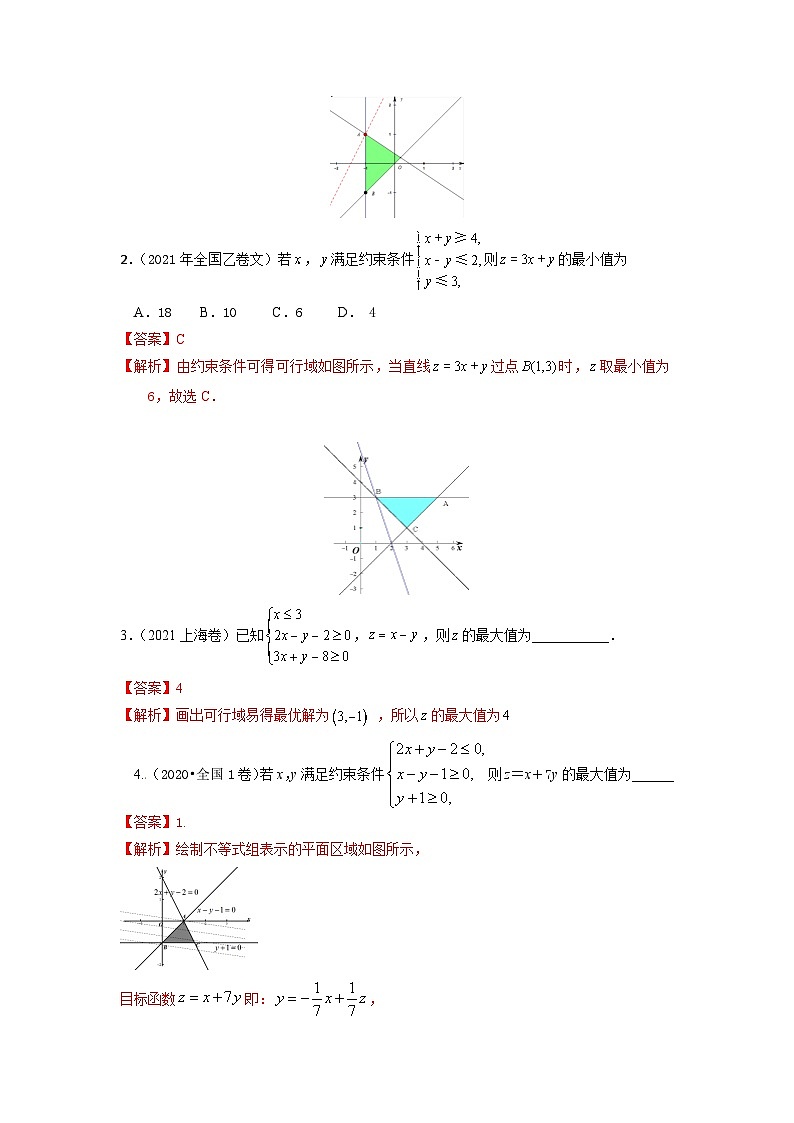
易错点10   不等式易错点1：线性规划求线性目标函数z＝ax＋by(ab≠0)的最值，当b＞0时，直线过可行域且在y轴上截距最大时，z值最大，在y轴截距最小时，z值最小；当b＜0时，直线过可行域且在y轴上截距最大时，z值最小，在y轴上截距最小时，z值最大.易错点2：基本不等式均值不等式（当仅当a=b时取等号）注意：①一正二定三相等；②变形：（当仅当a=b时取等号）易错点3：绝对值不等式(1)用零点分段法解绝对值不等式的步骤：①求零点；②划区间、去绝对值号；③分别解去掉绝对值的不等式；④取每个结果的并集，注意在分段时不要遗漏区间的端点值．(2)用图象法、数形结合可以求解含有绝对值的不等式，使得代数问题几何化，既通俗易懂，又简洁直观，是一种较好的方法．易错点4：柯西不等式(1)使用柯西不等式证明的关键是恰当变形，化为符合它的结构形式，当一个式子与柯西不等式的左边或右边具有一致形式时，就可使用柯西不等式进行证明．(2)利用柯西不等式求最值的一般结构为(a＋a＋…＋a)(＋＋…＋)≥(1＋1＋…＋1)2＝n2.在使用柯西不等式时，要注意右边为常数且应注意等号成立的条件．题组1 线性规划1．（2021浙江卷） 若实数 满足约束条件 ，则 的最小值是（     ）. A． B．  C．   D．【答案】B【解析】如图，画出可行域，显然过点时，取到最小值，即， 故选B．2．（2021年全国乙卷文）若，满足约束条件则的最小值为A．18    B．10     C．6     D． 4【答案】C【解析】由约束条件可得可行域如图所示，当直线过点时，取最小值为6，故选C． 3．（2021上海卷）已知，，则的最大值为___________．【答案】4【解析】画出可行域易得最优解为 ，所以的最大值为4.（2020•全国1卷）若x，y满足约束条件则z＝x＋7y的最大值为______【答案】1.【解析】绘制不等式组表示的平面区域如图所示，目标函数即：，其中z取得最大值时，其几何意义表示直线系在y轴上的截距最大，据此结合目标函数的几何意义可知目标函数在点A处取得最大值，联立直线方程：，可得点A的坐标为：，据此可知目标函数的最大值为：.故答案为：1．题组2 基本不等式5．（2021年全国乙卷文）下列函数最小值为4的是（   ）A．  B． C．  D．【答案】C【解析】由题意可知A的最小值为3，B的等号成立条件不成立，D无最小值．6．（2020年新全国1山东）已知a＞0，b＞0，且a＋b＝1，则（    ）A.  B. C.  D. 【答案】ABD【解析】对于A，，当且仅当时，等号成立，故A正确；对于B，，所以，故B正确；对于C，，当且仅当时，等号成立，故C不正确；对于D，因为，所以，当且仅当时，等号成立，故D正确；故选：ABD7.（2020年天津卷）已知，且，则的最小值为_____．【答案】4【解析】，,，当且仅当＝4时取等号，结合,解得，或时，等号成立.故答案为：8.（2020年江苏卷）已知，则的最小值是_______．【答案】【解析】∵,∴且∴，当且仅当，即时取等号.∴的最小值为.故答案为：.题组3 含绝对值不等式9.（2021年全国甲卷）已知函数，.（1）画出和的图像.（2）若，求的取值范围.【答案】见解析【解析】易知则和的图像为（1）由（1）中的图可知，是左右平移个单位得到的结果，向右平移不合题意，向左平移至的右支过点曲线，上的点为临界状态，此时右支的解析式为，由点在可知，解得，若要满足题意，则要再向左平移，则,则的取值范围为10.（2021年全国乙卷）已知函数.（1）当时，求不等式≥的解集；（2）若，求的取值范围.【答案】（1）；（2）【解析】（1）当时，≥≥，当≤时，不等式≥，解得≤；当时，不等式≥，解得；当≥时，不等式≥，解得≥.综上，原不等式的解集为.（2）若，即，因为≥（当且仅当≤时，等号成立），所以，所以，即或，解得.11．（2020全国Ⅰ文理22）已知函数．（1）画出的图像；（2）求不等式的解集．【解析】（1）∵，作出图像，如图所示：（2）将函数的图像向左平移个单位，可得函数的图像，如图所示：由，解得，∴不等式的解集为．12．（2020江苏23）设，解不等式．【答案】【解析】或或，或或，∴解集为．题组4 格西不等式13．（2021年浙江卷）已知平面向量，，满足，，，．记平面向量在，方向上的投影分别为，，在方向上的投影为，则的最小值是　  　．【答案】【解析】设，，（当且仅当时，即时，取得等号）．14．（2019全国I文理23）已知a，b，c为正数，且满足abc=1．证明：（1）；（2）．【答案】（1）证明见解析（2）证明见解析．【解析】（1）因为，又， 故有，∴．（2）因为为正数且，故有=24．∴． 1.下列不等式恒成立的是（）A.                B.C.              D.【解析】B2．若，，则一定有A．       B．        C．         D．【解析】由，又，由不等式性质知：，所以3．已知，，，则的最小值为（　　）A．20 B．24 C．25 D．28【解析】由题意，当且仅当，即时等号成立．故选：C．4．若实数、满足不等式组，则的取值范围为（    ）A． B． C． D．【解析】如图，绘出不等式组表示的平面区域，然后通过平移直线即可得出过点时取得最小值，无最大值，则的取值范围为，故选：C. 5．设，满足约束条件，则的取值范围是A．[–3,0]            B．[–3,2]                  C．[0,2]               D．[0,3]【解析】不等式组的可行域如图，目标函数的几何意义可得函数在点 处取得最小值 . 在点 处取得最大值，选B．6.（多选题）已知a＞0，b＞0，且a＋b＝1，则（    ）A.  B. C.  D. 【解析】对于A，，当且仅当时，等号成立，故A正确；对于B，，所以，故B正确；对于C，，当且仅当时，等号成立，故C不正确；对于D，因为，所以，当且仅当时，等号成立，故D正确；故选：ABD7.若满足约束条件，则的最小值为____________.【解析】画出不等式组表示的平面区域，如图阴影部分，将化为，则数形结合可得，当直线过点时，取得最小值为.故答案为：8.设，，，则的最小值为__________.【解析】，，，
而.
由基本不等式有，所以（当且仅当时，即，时，等号成立）.
所以，，所以的最小值为.9．已知函数．(1)求不等式的解集；(2)若不等式的解集非空，求的取值范围．【解析】（1），当时，无解；当时，由得，，解得；当时，由解得．∴的解集为．（2）由得，而，且当时，，故m的取值范围为．10．设均为正数，且，证明：（Ⅰ）；（Ⅱ）．【解析】（Ⅰ）得，由题设得，即，∴，即．（Ⅱ）∵，∴，即，∴．