2020-2021学年江苏省常州市溧阳市高一（下）期末数学试卷

这是一份2020-2021学年江苏省常州市溧阳市高一（下）期末数学试卷，共27页。试卷主要包含了单项选择题，多项选择题，填空题，解答题等内容，欢迎下载使用。
2020-2021学年江苏省常州市溧阳市高一（下）期末数学试卷
一、单项选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.
1．（5分）某种彩票中奖的概率为，这是指　　
A．买10000张彩票一定能中奖
B．买10000张彩票只能中奖1次
C．若买9999张彩票未中奖，则第10000张必中奖
D．买一张彩票中奖的可能性是
2．（5分）已知，则　　
A． B． C． D．
3．（5分）甲、乙两个同学下棋，若甲获胜的概率为0.2，甲不输的概率为0.7，则甲、乙下成和棋的概率为　　
A．0.5 B．0.7 C．0.9 D．0.4
4．（5分）在中，若，则的形状是　　
A．等腰三角形 B．直角三角形
C．等腰或直角三角形 D．等边三角形
5．（5分）已知数据，，，的平均数为2，方差为3，那么数据，，，的平均数和方差分别为　　
A．2，3 B．5，6 C．5，12 D．4，12
6．（5分）已知，则的值是　　
A． B． C． D．
7．（5分）如图，在同一个平面内，向量，，的模分别为1，，，与的夹角为，且，与的夹角为．若，则　　

A．3 B． C． D．
8．（5分）在棱长为2的正方体中，点，分别是棱，的中点，动点在正方形（包括边界）内运动．若平面，则的最小值是　　

A．2 B． C． D．
二、多项选择题：本题共4小题，每小题5分，共20分.在每小题给出的选项中，有多项符合题目要求.全部选对的得5分，部分选对的得2分，有选错的得0分.
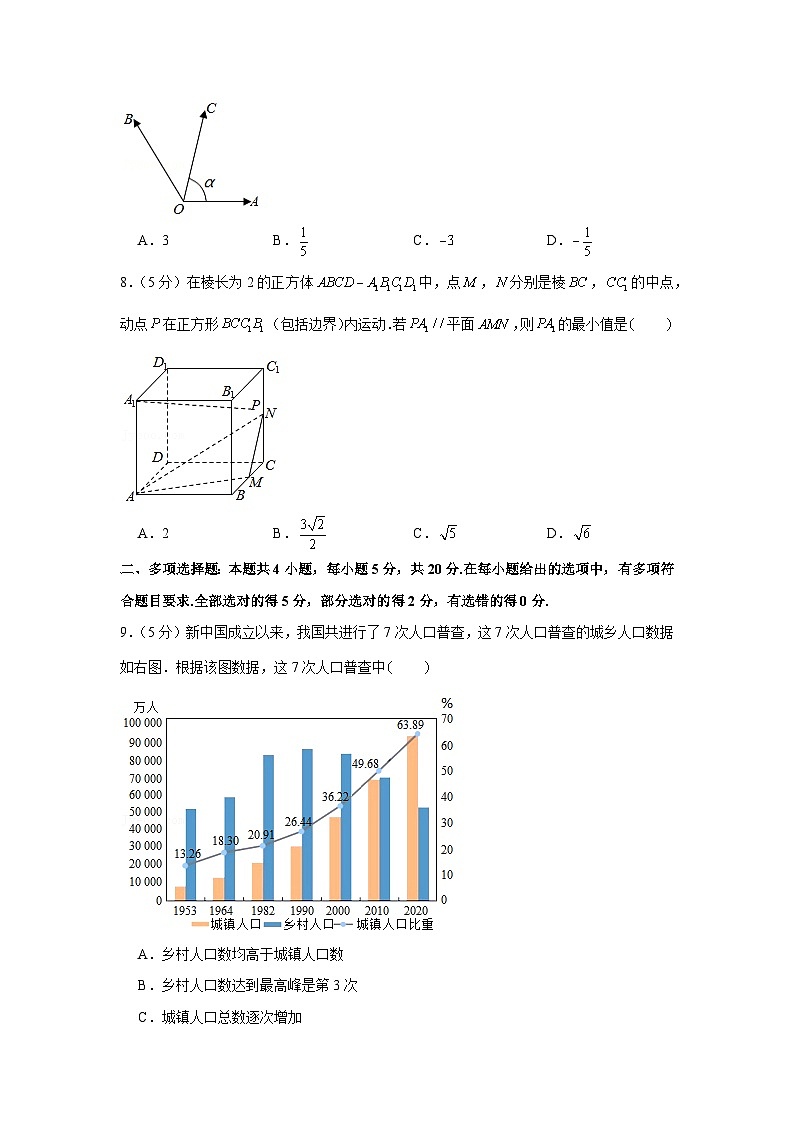
9．（5分）新中国成立以来，我国共进行了7次人口普查，这7次人口普查的城乡人口数据如右图．根据该图数据，这7次人口普查中　　

A．乡村人口数均高于城镇人口数
B．乡村人口数达到最高峰是第3次
C．城镇人口总数逐次增加
D．和前一次相比，城镇人口比重增量最大的是第7次
10．（5分）下列结论正确的是　　
A．若复数满足，则为纯虚数
B．若复数，满足，则
C．若复数满足，则
D．若复数满足，则，
11．（5分）如图是一个正方体的平面展开图，则在该正方体中　　

A． B．
C．与成角 D．与平面所成角为
12．（5分）“奔驰定理”是平面向量中一个非常优美的结论，因为这个定理对应的图形与“奔驰” 的很相似，故形象地称其为“奔驰定理”．奔驰定理：已知是内的一点，，，的面积分别为，，，则．若是锐角内的一点，，，是的三个内角，且点满足．则　　

A．为的外心
B．
C．
D．
三、填空题：本题共4个小题，每小题5分，共20分。
13．（5分）设为实数，若向量，，且，则的值为 　　．
14．（5分）满足等式的数组有无穷多个，试写出一个这样的数组 　　．
15．（5分）《九章算术》是我国古代数学名著，它在几何学中的研究比西方早1000多年．在《九章算术》中，将底面为矩形且一侧棱垂直于底面的四棱锥称为阳马．如图是阳马，平面，，，，则该阳马的外接球的表面积为 　　．

16．（5分）甲、乙二人做射击游戏，甲、乙射击击中与否是相互独立事件．规则如下：若射击一次击中，则原射击人继续射击；若射击一次不中，就由对方接替射击．已知甲、乙二人射击一次击中的概率均为，且第一次由甲开始射击．
①求前3次射击中甲恰好击中2次的概率　 　；
②求第4次由甲射击的概率　 　．
四、解答题：本题共6小题，共70分。解答应写出文字说明，证明过程或演算步骤。
17．（10分）已知复数满足，且的虚部为，在复平面内所对应的点在第四象限．
（1）求；
（2）若，在复平面上对应的点分别为，，为坐标原点，．
18．（12分）如图，在三棱锥中，，，，为的中点，为上一点，且平面，．求证：
（1）直线平面；
（2）．

19．（12分）某中学高一年级举行了一次数学竞赛，从中随机抽取了一批学生的成绩．经统计，这批学生的成绩全部介于50至100之间，将数据按照，，，，，，，，，的分组作出频率分布直方图如图所示．
（1）求频率分布直方图中的值，并估计本次竞赛成绩的第80百分位数；
（2）若按照分层随机抽样从成绩在，，，的两组中抽取6人，再从这6人中随机抽取2人，求至少有1人的成绩在，内的概率．

20．（12分）已知在中，角，，的对边分别为，，，．
（1）若，求的值；
（2）若点在边上，且，，求面积的最大值．
21．（12分）已知在正三棱柱中，，是棱的中点．
（1）求证：平面平面；
（2）设，求三棱锥的体积；
（3）若把平面与平面所成的锐二面角为时的正三棱柱称为“黄金棱柱”，请判断此三棱柱是否为“黄金棱柱”，并说明理由．

22．（12分）如图，某小区准备将闲置的一直角三角形地块开发成公共绿地，图中．设计时要求绿地部分（如图中阴影部分所示）有公共绿地走道，且两边是两个关于走道对称的三角形和△．现考虑方便和绿地最大化原则，要求点与点，均不重合，落在边上且不与端点，重合，设．
（1）若，求此时公共绿地的面积；
（2）为方便小区居民的行走，设计时要求，的长度最短，求此时绿地公共走道的长度．


2020-2021学年江苏省常州市溧阳市高一（下）期末数学试卷
参考答案与试题解析
一、单项选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.
1．（5分）某种彩票中奖的概率为，这是指　　
A．买10000张彩票一定能中奖
B．买10000张彩票只能中奖1次
C．若买9999张彩票未中奖，则第10000张必中奖
D．买一张彩票中奖的可能性是
【分析】根据事件的运算及概率的性质对四个说法进行验证即可得出正确的说法的个数，选出正确答案．
【解答】解：如果某种彩票的中奖概率为，则买10000张这种彩票仍然是随机事件，即买10000张彩票，可能有多张中奖，也可能不能中奖，排除，；
若买9999张彩票未中奖，则第10000张也是随机事件，且发生概率仍然是，故错误，这里的中奖的概率为，是指买一张彩票中奖的可能性是，故正确．
故选：．
【点评】本题考查概率的意义及事件的运算，属于基本概念题．
2．（5分）已知，则　　
A． B． C． D．
【分析】把代入，再由复数代数形式的乘除运算化简得答案．
【解答】解：，
．
故选：．
【点评】本题考查复数代数形式的乘除运算，考查复数的基本概念，是基础题．
3．（5分）甲、乙两个同学下棋，若甲获胜的概率为0.2，甲不输的概率为0.7，则甲、乙下成和棋的概率为　　
A．0.5 B．0.7 C．0.9 D．0.4
【分析】利用互斥事件的概率加法公式即可得出．
【解答】解：甲不输包含甲、乙两人下成和棋与甲获胜，
且甲、乙两人下成和棋与甲获胜是互斥事件，
甲、乙下成和棋的概率．
故选：．
【点评】本题考查互斥事件及其概率加法公式，属于基础题．
4．（5分）在中，若，则的形状是　　
A．等腰三角形 B．直角三角形
C．等腰或直角三角形 D．等边三角形
【分析】由正弦定理把已知的等式化边为角，结合两角和的正弦化简，求出，进一步求得，即可得解．
【解答】解：由，结合正弦定理可得：，
，可得：，
，则的形状为等腰三角形．
故选：．
【点评】本题考查正弦定理的应用，考查了两角和与差的三角函数，考查了转化思想，属于基础题．
5．（5分）已知数据，，，的平均数为2，方差为3，那么数据，，，的平均数和方差分别为　　
A．2，3 B．5，6 C．5，12 D．4，12
【分析】利用平均数与方差的运算性质求解即可．
【解答】解：因为数据，，，的平均数为2，方差为3，
所以数据，，，的平均数为，
方差为．
故选：．
【点评】本题考查了平均数与方差的求解，解题的关键是掌握平均数与方差的运算性质，属于基础题．
6．（5分）已知，则的值是　　
A． B． C． D．
【分析】根据已知条件，运用三角函数的两角和公式，可得，对等式两边同时平方，再结合二倍角公式，即可求解．
【解答】解：，
，
，对等式两边平方，可得，
，解得．
故选：．
【点评】本题考查了三角函数的两角和公式，以及二倍角公式，需要学生熟练掌握公式，属于基础题．
7．（5分）如图，在同一个平面内，向量，，的模分别为1，，，与的夹角为，且，与的夹角为．若，则　　

A．3 B． C． D．
【分析】由已知得出为锐角，即可求出的值，然后将已知向量的关系式两边同时点乘向量，化简即可求解．
【解答】解：由已知可得角为锐角，则由，
解得，
因为，所以，
即，则，
所以，
故选：．
【点评】本题考查了平面向量基本定理的应用，涉及到向量的数量积的运算性质以及三角函数的应用，属于基础题．
8．（5分）在棱长为2的正方体中，点，分别是棱，的中点，动点在正方形（包括边界）内运动．若平面，则的最小值是　　

A．2 B． C． D．
【分析】取的中点，的中点，连结，，，取中点，连结，推导出平面平面，从而点的轨迹是线段，由此能求出的长度范围，即可求出其最小值．
【解答】解：取的中点，的中点，连结，，，取中点，连结，
点，分别是棱长为2的正方体中棱，的中点，
，，
，，
平面平面，
动点在正方形（包括边界）内运动，且面，
点的轨迹是线段，
，，
，
当与重合时，的长度取最小值，为，
当与（或重合时，的长度取最大值，为．
的长度范围为，．
即其最小值为：
故选：．

【点评】本题考查线段长度的取值范围的求法，考查空间中线线、线面、面面间的位置关系等基础知识，考查运算求解能力，是中档题．
二、多项选择题：本题共4小题，每小题5分，共20分.在每小题给出的选项中，有多项符合题目要求.全部选对的得5分，部分选对的得2分，有选错的得0分.
9．（5分）新中国成立以来，我国共进行了7次人口普查，这7次人口普查的城乡人口数据如右图．根据该图数据，这7次人口普查中　　

A．乡村人口数均高于城镇人口数
B．乡村人口数达到最高峰是第3次
C．城镇人口总数逐次增加
D．和前一次相比，城镇人口比重增量最大的是第7次
【分析】利用题中条形图和折线图中的数据信息以及变化趋势，对四个选项逐一分析判断即可．
【解答】解：对于，2020年，城镇人口比重为，即城镇人口数高于乡村人口数，故选项错误；
对于，由统计图可知，乡村人口数达到最高峰是第4次，故选项 错误；
对于，由统计图可知，城镇人口总数逐次增加，故选项正确；
对于，第二次与第一次相比，城镇人口比重增量为，
第三次与第二次相比，城镇人口比重增量为，
第四次与第三次相比，城镇人口比重增量为，
第五次与第四次相比，城镇人口比重增量为，
第六次与第五次相比，城镇人口比重增量为，
第七次与第六次相比，城镇人口比重增量为，
和前一次相比，城镇人口比重增量最大的是第7次，故选项正确．
故选：．
【点评】本题考查了条形图和折线图的应用，读懂统计图并能从统计图得到必要的信息是解决问题的关键，属于基础题．
10．（5分）下列结论正确的是　　
A．若复数满足，则为纯虚数
B．若复数，满足，则
C．若复数满足，则
D．若复数满足，则，
【分析】直接利用复数的运算，复数的模，复数的几何意义结合选项判断各选项即可．
【解答】解：对于：设，则，
由于，所以，故，
当时，为实数，故错误；
对于：设，，
所以，，
由于复数，满足，
所以，
则，整理得．
所以，故错误；
对于：设，所以，
由于复数满足，所以，故，故正确；
对于：设，因为，所以，
所以该曲线为以为圆心，1为半径的圆，
故，，所以，，故正确．
故选：．
【点评】本题考查复数的运算，复数的模和复数的几何意义，考查运算能力，属于基础题．
11．（5分）如图是一个正方体的平面展开图，则在该正方体中　　

A． B．
C．与成角 D．与平面所成角为
【分析】由正方体的平面展开图还原原正方体，再由正方体的结构特征结合空间角的概念逐一分析四个选项得答案．
【解答】解：由正方体的平面展开图还原原正方体如图，

由正方体的结构特征可知，与异面垂直，故错误；
，而为在平面上的射影，，故正确；
连接，由，，可得四边形为平行四边形，则，
为异面直线与所成角，连接，可得为等边三角形，得与成角，
故正确；
平面，为与平面所成角为，故正确．
故选：．
【点评】本题考查空间角的概念与求法，考查空间想象能力与思维能力，考查运算求解能力，是中档题．
12．（5分）“奔驰定理”是平面向量中一个非常优美的结论，因为这个定理对应的图形与“奔驰” 的很相似，故形象地称其为“奔驰定理”．奔驰定理：已知是内的一点，，，的面积分别为，，，则．若是锐角内的一点，，，是的三个内角，且点满足．则　　

A．为的外心
B．
C．
D．
【分析】由可得为的垂心；结合与三角形内角和等于可证明选项；结合选项结论证明即可证明选项，利用奔驰定理证明可证明选项．
【解答】解：因为，
同理，，故为的垂心，故错误；
，所以，
又，所以，
又，所以，故正确；
故，同理，
延长交与点，则
，
同理可得，所以，故正确；

，
同理可得，所以，
又，所以，故正确．
故选：．

【点评】本题考查三角形垂心的性质，考查平面向量的线性运算，考查数学运算和直观想象的核心素养，属于难题．
三、填空题：本题共4个小题，每小题5分，共20分。
13．（5分）设为实数，若向量，，且，则的值为 　　．
【分析】利用向量共线，求解，然后求解向量的数量积即可．
【解答】解：向量，，且，
可得，解得，所以，，．
故答案为：．
【点评】本题考查向量共线的应用，向量的数量积的求法，是基础题．
14．（5分）满足等式的数组有无穷多个，试写出一个这样的数组 　　．
【分析】当时，等式，可化简为，求出满足等式的一个值，即可求解．
【解答】解：当时，等式，可化简为，
，
可取，
满足等式的数组可取．
故答案为：．
【点评】本题考查正切函数的取值，属于基础题．
15．（5分）《九章算术》是我国古代数学名著，它在几何学中的研究比西方早1000多年．在《九章算术》中，将底面为矩形且一侧棱垂直于底面的四棱锥称为阳马．如图是阳马，平面，，，，则该阳马的外接球的表面积为 　　．

【分析】把四棱锥放置在长方体中，求出长方体外接球的表面积得答案．
【解答】解：把四棱锥放置在长方体中，

则长方体的外接球即为四棱锥的外接球，
，，，长方体的对角线长为，
则长方体的外接球的半径，
该“阳马”外接球的表面积为．
故答案为：．
【点评】本题考查多面体的外接球，训练了分割补形法，考查运算求解能力，是中档题．
16．（5分）甲、乙二人做射击游戏，甲、乙射击击中与否是相互独立事件．规则如下：若射击一次击中，则原射击人继续射击；若射击一次不中，就由对方接替射击．已知甲、乙二人射击一次击中的概率均为，且第一次由甲开始射击．
①求前3次射击中甲恰好击中2次的概率　　；
②求第4次由甲射击的概率　 　．
【分析】①由题意可得第一次射击，甲击中目标，第二次也击中目标，但第三次没有击中目标，根据相互独立事件的概率乘法公式，计算求的结果．
②分4种情况讨论，求得第4次由甲射击的概率．
【解答】解：①由题意，前3次射击中甲恰好击中2次，即前2次甲都击中目标，但第三次没有击中目标，故它的概率为．
②第4次由甲射击包括甲连续射击3次且都击中；第一次甲射击击中，但第二次没有击中，第三次由乙射击没有击中；
第一次甲射击没有击中，且乙射击第二次击中，但第三次没有击中；
第一次甲射击没有击中，且乙射击第二次没有击中，第三次甲射击击中；
故这件事的概率为，
故答案为：；．
【点评】本题主要考查相互独立事件的概率乘法公式的应用，体现了分类讨论的数学思想，属于中档题．
四、解答题：本题共6小题，共70分。解答应写出文字说明，证明过程或演算步骤。
17．（10分）已知复数满足，且的虚部为，在复平面内所对应的点在第四象限．
（1）求；
（2）若，在复平面上对应的点分别为，，为坐标原点，．
【分析】（1）由题意设，利用列式求得值，则可求；
（2）分别求出，，的坐标，得到的坐标，再由数量积求夹角可得．
【解答】解：（1）设，
，，
得或，
又在复平面内所对应的点在第四象限，
；
（2），
，，，
，，
则，
．
【点评】本题考查复数的代数表示法及其几何意义，考查复数模的求法，训练了利用数量积求向量的夹角，是中档题．
18．（12分）如图，在三棱锥中，，，，为的中点，为上一点，且平面，．求证：
（1）直线平面；
（2）．

【分析】（1）根据线面平行的性质定理，由平面，推出，再由线面平行的判定定理，得证；
（2）易知，由勾股定理可证，从而知，再由线面垂直的判定定理证明平面，进而得证．
【解答】证明：（1）平面，平面，平面平面，
，
又平面，平面，
平面．
（2）由（1）得，，
又是的中点，
是的中点，
，
又，，
，即，
，，
，且是的中点，，
又，平面，平面，
平面，
平面，
故
【点评】本题考查空间中线与面的位置关系，熟练掌握线与面平行、垂直的判定定理或性质定理是解题的关键，考查空间立体感、推理论证能力，属于中档题．
19．（12分）某中学高一年级举行了一次数学竞赛，从中随机抽取了一批学生的成绩．经统计，这批学生的成绩全部介于50至100之间，将数据按照，，，，，，，，，的分组作出频率分布直方图如图所示．
（1）求频率分布直方图中的值，并估计本次竞赛成绩的第80百分位数；
（2）若按照分层随机抽样从成绩在，，，的两组中抽取6人，再从这6人中随机抽取2人，求至少有1人的成绩在，内的概率．

【分析】（1）利用频率之和为1，列式求，由百分位数的定义求解第80百分位数即可；
（2）先求出从，和，中抽取的人数，然后利用列举法求出总的基本事件数以及符合条件的基本事件数，由古典概型的概率公式求解即可．
【解答】解：（1）由题意得，，
所以，
因为，，，，，
所以成绩在80（分以下的频率为，
成绩在90（分以下的频率为，
所以第80百分位数，即．
（2）因为，，，的频率之比为，
所以从，中随机抽取人，从，中随机抽取
从，中抽取的2人记为，，从，中抽取的4人记为1，2，3，4，
从这6人中随机抽取2人的样本空间为，13，14，，，23，24，，，34，，，，，，共有15个样本点，
设事件表示“至少有1人的成绩在，内”，
则，，，，，，，，共有9个样本点，
所以至少有1人在，内的概率为．
【点评】本题考查了频率分布直方图的应用，百分位数的定义以及古典概型概率公式的运用，考查了逻辑推理能力与化简运算能力，属于基础题．
20．（12分）已知在中，角，，的对边分别为，，，．
（1）若，求的值；
（2）若点在边上，且，，求面积的最大值．
【分析】（1）根据已知条件，运用余弦定理，可推得，再结合三角函数的同角公式和余弦函数的两角差公式，即可求解．
（2）法一，由，可推得，对等式两边同时平方，并结合均值不等式和三角形面积公式，即可求解．
法二，由于，可得，，在和，分别运用余弦定理，可得
①，在中，运用余弦定理得，②，联立①②，并结合均值不等式，可得，再结合三角形面积公式，即可求解．
【解答】解：（1）由余弦定理得，，
整理可得，，

又，
，
，
又，
，
故．
（2）法，
，
，
即，
．当且仅当，等号成立，
又，
面积的最大值为．
法，
，
在中，由余弦定理得，，
在中，由余弦定理得，，
又，所以，
整理得，①，
又在中，由余弦定理得，②，
由①②得，，
．当且仅当，等号成立，
又，
面积的最大值为．
【点评】本题主要考查了余弦定理和向量的运用．考查了学生对三角函数基础知识的综合运用，属于中档题．
21．（12分）已知在正三棱柱中，，是棱的中点．
（1）求证：平面平面；
（2）设，求三棱锥的体积；
（3）若把平面与平面所成的锐二面角为时的正三棱柱称为“黄金棱柱”，请判断此三棱柱是否为“黄金棱柱”，并说明理由．

【分析】（1）证法1：取为的中点，利用等腰三角形证明，，得出平面，证明平面平面．
证法2：取为的中点，利用菱形的性质证明，，得出平面，证明平面平面．
（2）解法1：利用等体积法计算即可．
解法2：利用三棱锥体积公式计算．
（3）延长交的延长线于点，连接，为平面与平面的交线，为平面与平面所成二面角的平面角，判断是否为即可．
【解答】解：（1）证明：连接与交于点，连接，如图1所示：

证法1：因为为正三棱柱，且是棱的中点，
所以，且为平行四边形，
所以为的中点，因此．
同理得，则，平面，，所以平面；
而平面，所以平面平面．
证法2：因为为正三棱柱，得为正△为平行四边形，
又，所以为菱形，
所以，
由为菱形得为的中点，
又是棱的中点，得，
所以，平面，平面，，
所以平面，
又平面，所以平面平面．
（2）解法1：由（1）法1得平面，
所以，
又在△中，，，
所以．
解法2：由（1）法2得平面，
所以，
又在△中，，
在△中，，，
所以；
所以．
（3）延长交的延长线于点，连接，如图2所示：

则为平面与平面的交线，
因为，又为的中点，所以为的中点，
即，则，
因为正三棱柱，
所以平面，平面，
所以，，、平面，
所以平面，又平面，
所以，又，
所以为平面与平面所成二面角的平面角；
若此正三棱柱为“黄金棱柱”，则，
可得，即，
与条件矛盾，所以此三棱柱不能成为“黄金棱柱”．
【点评】本题考查了空间中的垂直关系应用问题，也考查了棱锥的体积和二面角的计算问题，是中档题．
22．（12分）如图，某小区准备将闲置的一直角三角形地块开发成公共绿地，图中．设计时要求绿地部分（如图中阴影部分所示）有公共绿地走道，且两边是两个关于走道对称的三角形和△．现考虑方便和绿地最大化原则，要求点与点，均不重合，落在边上且不与端点，重合，设．
（1）若，求此时公共绿地的面积；
（2）为方便小区居民的行走，设计时要求，的长度最短，求此时绿地公共走道的长度．

【分析】（1）由题意可知，故为等边三角形，根据与的关系得出，代入面积公式计算；
（2）用 表示出，利用正弦定理得出关于的函数，利用三角恒等变换求出取得最小值对应的值，再计算的长．
【解答】解：（1）△，，
，．
，
，，，，
是等边三角形，
．
（2），，
．
，即，
．
在中，由正弦定理可得：，
，
令．
，当即时取最大值，
当时最短，此时是等边三角形，．
【点评】本题考查了解三角形的实际应用，正弦定理及三角恒等变换，属于中档题．
声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布
日期：2021/8/23 17:47:31；用户：高中数学12；邮箱：sztdjy76@xyh.com；学号：26722394