江西省南昌市第二中学2020-2021学年高一上学期期中考试数学试题 Word版含答案

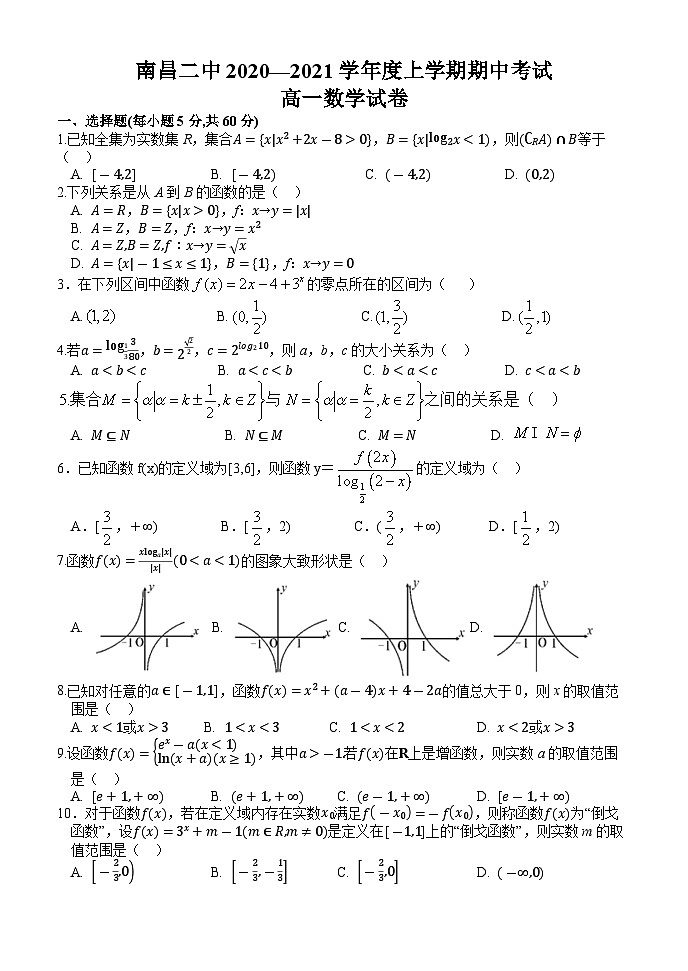
南昌二中2020—2021学年度上学期期中考试

高一数学试卷

一、选择题(每小题5分,共60分)

1.已知全集为实数集R，集合，，则等于（  ）

A.  B.      C.   D.

2.下列关系是从A到B的函数的是（  ）

A. ，，f：
B. ，，f：
C.
D. ，，f：

3．在下列区间中函数的零点所在的区间为（   ）

A.              B.             C.             D.

4.若，，，则a，b，c的大小关系为（  ）

A.         B.           C.        D.

A.    B.     C.        D.

6．已知函数f(x)的定义域为[3,6]，则函数y＝的定义域为（  ）

A．[，＋∞)         B．[，2)         C．(，＋∞)       D．[，2)

7.函数的图象大致形状是（  ）

A. B. C. D.

8.已知对任意的，函数的值总大于0，则x的取值范围是（  ）

A. 或     B.        C.      D. 或

9.设函数，其中若在上是增函数，则实数a的取值范围是（  ）

A.  B.      C.    D.

10．对于函数，若在定义域内存在实数满足，则称函数为“倒戈函数”，设是定义在上的“倒戈函数”，则实数m的取值范围是（  ）

A.  B.  C.    D.

11.设函数，若互不相等的实数满足，则的取值范围是（  ）

A.  B.  C.  D.

12.已知的图象关于直线对称，则的值域为（  ）

A.  B.  C.  D.

二、填空题(每小题5分,共20分)

13.已知幂函数在上单调递增，则m值为______．

14．函数的值域为______．

15．函数的定义域上的值域为，则t的可取范围为______．

16.已知，设，若存在不相等的实数a，b同时满足方程

和   ，则实数m的取值范围为______．

三、解答题(70分)

17．（本小题10分）求下列各式的值：

（1）.

（2）.

18．（本小题12分）已知集合．

（1）  

（2）

19.（本小题12分）已知函数是定义在区间上的奇函数，对于任意的都有．

（1）证明在定义域上单调递增;

（2）解不等式.
 

20. （本小题12分）已知函数，．
      （1）若函数的值域为R，求实数a的取值范围
      （2）函数，若对于任意的，都存在使得不等式成立，求实数k的取值范围
     

21.（本小题12分）已知函数是定义在R上的奇函数．

(1)求a的值；

(2)是否存在实数k，使得函数在区间上的取值范围是？若存在，求出实数k的取值范围；若不存在，请说明理由．

22.（本小题12分）已知，函数.

（1）当时，解不等式；

（2）若关于x的方程有两个不等的实数根，求a的取值范围.
 

高一数学期中考试参考答案

1. D解：或，，，
．故选：D．

2.B解：根据题意，依次分析选项：对于A，A中有元素0，在对应关系下，不在集合B中，不是函数；对于B，符合函数的定义，是从A到B的函数；
对于C，A中元素时，B中没有元素与之对应，不是函数；
对于D，A中任意元素，在对应关系下，不在集合B中，不是函数；故选：B．

3．D 由题意得，因为在其定义域内都为增函数，因此在上为增函数，通过观察发现，那么在必有零点，故选D.

4.C ，，．故选：C．

6．B   由题意得⇒⇒≤x<2，选B项．

7.C解：，且，由题意，，
所以函数是奇函数，图象关于原点对称，排除B、D；时，是单调减函数，排除A．故选：C．

8．A解：原题可转化为关于a的一次函数在上恒成立，只需或．

9.D 解： 由解析式知在单调递增，在也单调递增，
若在R 上是增函数，则，即，
因为函数在单调递增，且当时，y的值为e，
所以由，得．故选D．

10．A解：因为是定义在上的“倒戈函数”，所以存在满足，所以，所以，构造函数，，令，
，所以所以．故答案为  ．

11.D解：函数的图象，如图，不妨设，则，关于直线对称，故，且是图中线段AB上的点对应的横坐标，故，即，则的取值范围是：；即．故选D．

12.B  解：因为函数有两个零点，0，又因为其图象关于直线对称，所以2，3也是函数的两个零点，即，所以，令，则，所以，即的值域为．

13.2  幂函数在 上单调递增，
，且，解得，故答案为：2．

14．  因为

，所以，故应填.

15.解：函数的对称轴为，当时，，

当时，为增函数，可得当时，，可得，解得：，

故要使的定义域上的值域为，t的可取范围为．

16. 解：易知函数，的定义域均为R．由可得，函数是奇函数，所以若，必有，
所以方程有解，即有解，．令，则，时有解，
又函数在区间上单调递增，当时，，所以，即，
当且仅当时取等号，此时不合题意，故．

17．解：（1）

（2）

所以原式

18．解：（1）

.

（2)

 当时，即；  当时，；

 综上所述，实数的取值范围为．

19.解：(1)设，，∵m+n≠0，则x1≠x2，则，
∵f（x）是奇函数，∴f（-x2）=-f（x2），∴，不妨设，则，
由函数单调性的定义可得函数在区间[-1，1]上是增函数;

(2)由(1)知函数在区间[-1，1]上是增函数.又由，
得,解得．所以不等式的解集为．

20.解：1时，内函数有最大值，故函数值不可能取到全体正数，不符合题意；
当时，内函数是一次函数，内层函数值可以取遍全体正数，值域是R，符合题意；
当时，要使内函数的函数值可以取遍全体正数，只需要函数最小值小于等于0，
故只需，解得．综上得．
2由题意可得在恒成立，
则在有解，即在有解，
，综上，实数k的取值范围．
21.解：是定义在R上的奇函数，，从而得出，
（2）假设存在实数k，使之满足题意函数在上单调递增，为方程的两个根，即方程有两个不等的实根，
令，即方程有两个不等的正根，
．存在实数k，使得函数在上的取值范围是，并且实数k的取值范围是．

22.解：1当时，，由得，
得，即，解得或，
当时，不等式的解集为.
2由题意得，该问题等价于
，化简得，
即
当时，，不合题意，舍去；

当时，，不合题意，舍去．
当且时，且由，得且；由，得且依题意，若原方程由两个不等的实数根，则且故所求的取值范围为．