初中数学14.1.4 整式的乘法教学ppt课件

这是一份初中数学14.1.4 整式的乘法教学ppt课件，共28页。PPT课件主要包含了a+bm+n，+an，+bm，+bn，多项式乘以多项式等内容，欢迎下载使用。

为了把校园建设成为花园式的学 校，经研究决定将原有的长为a米， 宽为b米的足球场向宿舍楼方向加长 m米，向厕所方向加宽n米，扩建成为美化校园绿草地.你是学校的小主人，你能帮助学校计算出扩展后绿地的面积吗？
2. 能够运用多项式与多项式的乘法运算法则进行计算.
1. 理解并掌握多项式与多项式的乘法运算法则.
1.如何进行单项式与多项式乘法的运算？
(2)再把所得的积相加.
(1)将单项式分别乘以多项式的各项.
2.进行单项式与多项式乘法运算时，要注意什么?
即单项式要乘多项式的每一项.
(2)去括号时注意符号的变化.
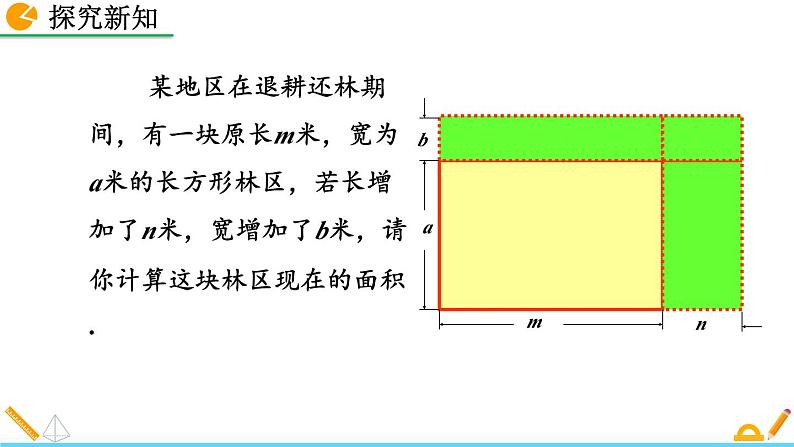
某地区在退耕还林期间，有一块原长m米，宽为a米的长方形林区，若长增加了n米，宽增加了b米，请你计算这块林区现在的面积.
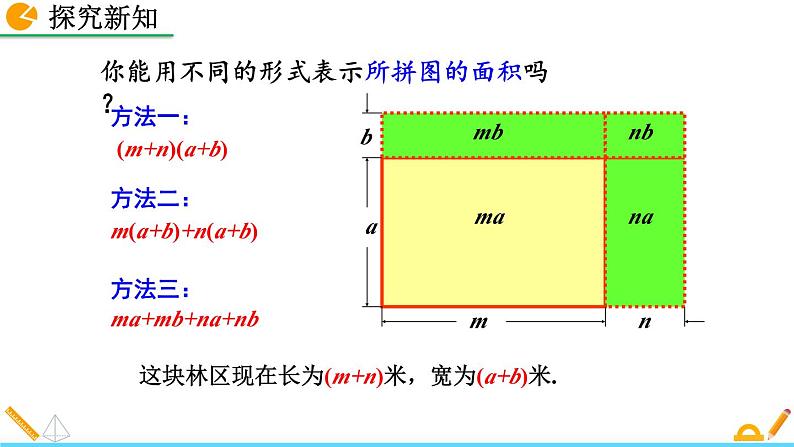
你能用不同的形式表示所拼图的面积吗？
这块林区现在长为(m+n)米，宽为(a+b)米.
m(a+b)+n(a+b)
ma+mb+na+nb
由于(m+n)(a+b)和(ma+mb+na+nb)表示同一块地的面积，故有：
(m+n)(a+b)=
如何进行多项式与多项式相乘的运算？
实际上，把(a+b)看成一个整体，有：
= ma+mb+na+nb
= m(a+b)+n(a+b)
若X=a+b，如何计算？
多项式与多项式相乘，先用一个多项式的每一项分别乘以另一个多项式的每一项，再把所得的积相加.
多乘多，来计算，多项式各项都见面，乘后结果要相加，化简、排列才算完.
例1 计算: (1)(3x+1)(x+2)； (2)(x–8y)(x–y)；
解： (1) 原式=3x·x+2·3x+1·x+1×2 =3x2+6x+x+2
(2) 原式=x·x–xy–8xy+8y2
=x2–9xy+8y2；
用多项式乘以多项式法则进行计算
(3) 原式=x·x2–x·xy+xy2+x2y–xy2+y·y2 =x3–x2y+xy2+x2y–xy2+y3 = x3+y3.
需要注意的几个问题：(1)漏乘；(2)符号问题；(3)最后结果应化成最简形式.
(3) (x+y)(x2–xy+y2).
快速训练: (1) (2x+1)(x+3); (2) (m+2n)(m+3n): (3) ( a – 1)2 ； (4) (a+3b)(a –3b ). (5) (x+2)(x+3); (6) (x–4)(x+1) (7) (y+4)(y–2); (8) (y–5)(y–3)
例2 先化简，再求值：(a–2b)(a2＋2ab＋4b2)–a(a–5b)(a＋3b)，其中a＝–1，b＝1.
当a＝–1，b＝1时，
解：原式＝a3–8b3–(a2–5ab)(a＋3b)
＝a3–8b3–a3–3a2b＋5a2b＋15ab2
＝–8b3＋2a2b＋15ab2.
原式＝–8＋2–15＝–21.
用多项式乘以多项式法则进行化简求值
先化简，再求值.(x–y)(x–2y) – (2x–3y)(x+2y)，其中 .
解：(x–y)(x–2y) – (2x–3y)(x+2y) =x2–2xy–xy+2y2–(2x2+4xy–3xy–6y2)
=x2–2xy–xy+2y2–2x2–xy+6y2
= –x2–4xy+8y2
当x= –2，y= 时，
原式= –6
例3 已知ax2＋bx＋1(a≠0)与3x–2的积不含x2项，也不含x项，求系数a、b的值．
解：(ax2＋bx＋1)(3x–2)
＝3ax3–2ax2＋3bx2–2bx＋3x–2，
∵积不含x2的项，也不含x的项，
方法总结：解决此类问题首先要利用多项式乘法法则计算出展开式，合并同类项后，再根据不含某一项，可得这一项系数等于零，再列出方程(组)解答．
选择题.(1)计算m2–(m+1)(m–5)的结果正确的是( )A.–4m–5B.4m+5C.m2–4m+5D.m2+4m–5(2)(1+x)(2x2+ax+1)的结果中x2项的系数为–2，则a的值为( )A.–2B.1C.–4D.以上都不对
1. 计算(a–2)(a+3)的结果是( )A．a2–6 B．a2+a–6C．a2+6 D．a2–a+6
2. 在矩形ABCD内，将两张边长分别为a和b(a＞b)的正方形纸片按图1，图2两种方式放置(图1，图2中两张正方形纸片均有部分重叠)，矩形中未被这两张正方形纸片覆盖的部分用阴影表示，设图1中阴影部分的面积为S1，图2中阴影部分的面积为S2．当AD–AB=2时，S2–S1的值为( 　)A．2a B．2b C．2a–2b D．–2b
2. 如果(x+a)(x+b)的结果中不含x的一次项，那么a、b满足(　　)A．a=b B．a=0 C．a=–b D．b=0
1. 计算(x–1)(x–2)的结果为(　　) A．x2+3x–2 B．x2–3x–2 C．x2+3x+2 D．x2–3x+2
3. 已知ab=a+b+1，则(a–1)(b–1)=_____．
4. 判别下列解法是否正确，若不正确，请说出理由.
5. 计算：(1)(x−3y)(x+7y)； (2)(2x + 5y)(3x−2y).
x2 +4xy–21y2；
(2) (2x +5 y)(3x−2y)
6x2 +11xy−10y2.
6.化简求值：(4x+3y)(4x–3y)+(2x+y)(3x–5y)，其中x=1，y= –2.
当x=1，y= –2时，原式=22×1–7×1×(–2)–14×(–2)2
=22+14 –56=–20.
解方程与不等式：①(x–3)(x–2)+18=(x+9)(x+1)；②(3x+6)(3x–6)＜9(x–2)(x+3)．
解：①原式去括号，得:x2–5x+6+18=x2+10x+9， 移项合并，得:15x=15， 解得:x=1； ②原式去括号，得:9x2–36＜9x2+9x–54， 移项合并，得:9x＞18， 解得:x＞2 ．
小东找来一张挂历画包数学课本．已知课本长a厘米，宽b厘米，厚c厘米，小东想将课本封面与封底的每一边都包进去m厘米，那么小东应在挂历画上裁下一块多大面积的长方形？
面积：(2m+2b+c)(2m+a)
解：(2m+2b+c)(2m+a)
= 4m2+2ma+4bm+2ab+2cm+ca.
答：小东应在挂历画上裁下一块 (4m2+2ma+4bm+2ab+2cm+ca)平方厘米的长方形.
多项式与多项式相乘，先用一个多项式的每一项分别乘以另一个多项式的每一项，再把所得的积相加.
(a+b)(m+n)=am+an+bm+bn
不要漏乘；正确确定各项符号；结果要最简.
实质上是转化为单项式乘多项式的运算.
(x–1)2在一般情况下不等于x2–12.