广东省揭阳市揭东区2022-2023学年八年级下学期期末考试数学试题

2022-2023学年度第二学期期末教学质量监测

八年级数学科试卷

温馨提示：1.将答案填写在答题卷上；2.考试时间为90分钟，满分120分。

一、选择题(本大题共10小题，每小题3分，共30分)

1．如图，以下四个图标中可以看作由“基本图案”经过平移得到的是（　　）

A．    B．    C． D．

2．若a＞b，则下列式子中正确的是（　　）

A． B．a﹣3＜b﹣3 C．﹣3a＜﹣3b D．b＞a

3．若等腰三角形的两边长分别为3和6，则该三角形的周长是（　　）

A．11 B．12 C．15 D．12或15

4．式子n2﹣1与n2+n的公因式是（　　）

A．n+1 B．n2 C．n D．n﹣1

5．化简：÷＝（　　）

A．1 B．x C． D．

6．到三角形三个顶点的距离都相等的点是（　　）

A．两条中线的交点               B．两条高的交点 

C．两条角平线的交点               D．两条边的垂直平分线的交点

7．下列各式从左到右的变形中，为因式分解的是（　　）

A．m（x+y）＝mx+my                      B．x2+16x+64＝（x+8）2 

C．x2+y2﹣36＝x2+（y+6）（y﹣6）          D．ay+by+c＝y（a+b）+c

8．如图，在△ABC中，AB边上的垂直平分线分别交边AC于点E，交边AB于点D，若AC的长为9cm，BE的长为6cm，则EC的长为（　　）

A．2cm B．3cm C．4cm D．5cm

9．如果关于x的分式方程有增根，则m的值为（　　）

A．1 B．﹣1 C．2 D．4

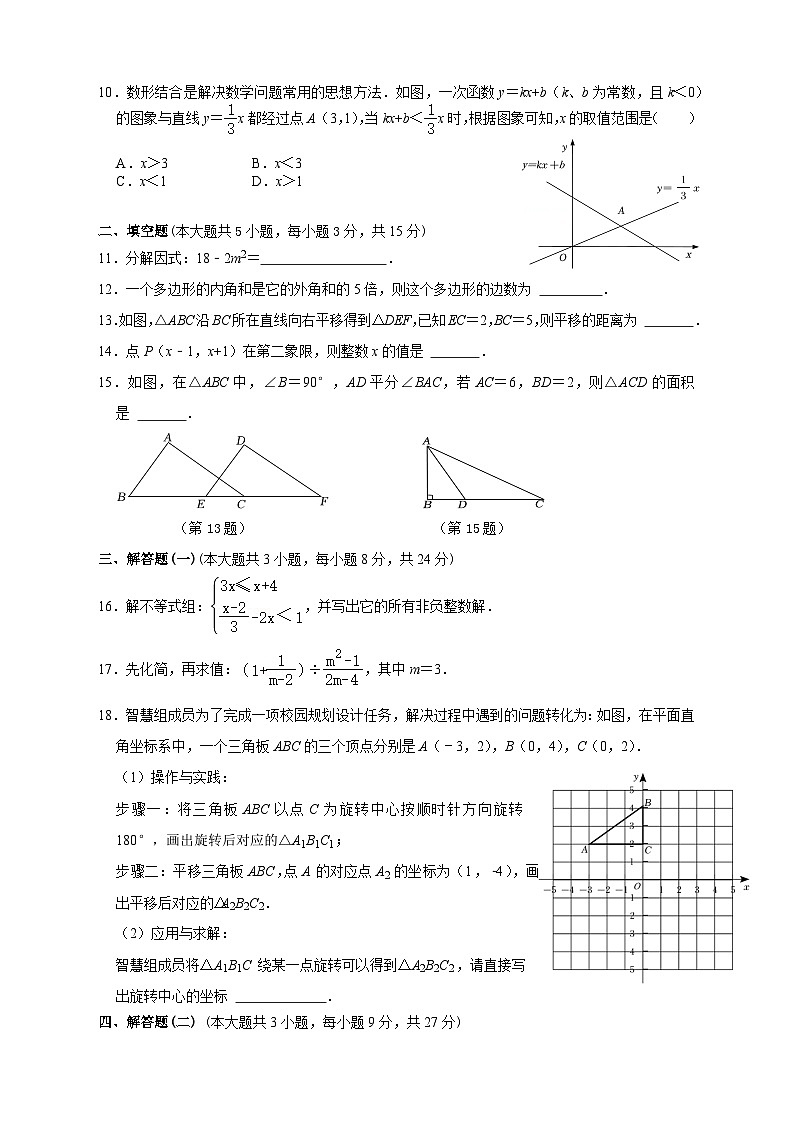
10．数形结合是解决数学问题常用的思想方法．如图，一次函数y＝kx+b（k、b为常数，且k＜0）的图象与直线y＝x都经过点A（3，1），当kx+b＜x时，根据图象可知，x的取值范围是（　　）

A．x＞3 B．x＜3 

C．x＜1 D．x＞1

二、填空题(本大题共5小题，每小题3分，共15分)

11．分解因式：18﹣2m2＝　              　．

12．一个多边形的内角和是它的外角和的5倍，则这个多边形的边数为 　     　．

13．如图，△ABC沿BC所在直线向右平移得到△DEF，已知EC＝2，BC＝5，则平移的距离为 　   　．

14．点P（x﹣1，x+1）在第二象限，则整数x的值是 　   　．

15．如图，在△ABC中，∠B＝90°，AD平分∠BAC，若AC＝6，BD＝2，则△ACD的面积是 　   　．

           （第13题）                          （第15题）

三、解答题(一)(本大题共3小题，每小题8分，共24分)

16．解不等式组：，并写出它的所有非负整数解．

17．先化简，再求值：，其中m＝3．

18．智慧组成员为了完成一项校园规划设计任务，解决过程中遇到的问题转化为：如图，在平面直角坐标系中，一个三角板ABC的三个顶点分别是A（﹣3，2），B（0，4），C（0，2）．

（1）操作与实践：

步骤一：将三角板ABC以点C为旋转中心按顺时针方向旋转180°，画出旋转后对应的△A1B1C1；

步骤二：平移三角板ABC，点A的对应点A2的坐标为（1，﹣4），画出平移后对应的△A2B2C2．

（2）应用与求解：

智慧组成员将△A1B1C绕某一点旋转可以得到△A2B2C2，请直接写出旋转中心的坐标 　         　．

四、解答题(二) (本大题共3小题，每小题9分，共27分)

19．疫情过后，今年云南旅游市场强劲复苏．某旅行社今年春节租用A、B两种客房，用4800元租到A客房的数量与用4200元租到B客房的数量相同，今年每间A客房的租金比每间B客房的租金多30元，分别求今年该旅行社租用的A、B两种客房每间客房的租金．

20．如图，已知点E、F为平行四边形ABCD对角线BD上两点，且∠BAF＝∠DCE，连接AE，CF．求证：（1）AF＝CE；（2）四边形AECF为平行四边形．

21．在学习对复杂多项式进行因式分解时，老师示范了如下例题：

完成下列任务：（1）例题中第二步到第三步运用了因式分解的 　   　；（填序号）

①提取公因式；②平方差公式；③两数和的完全平方公式；④两数差的完全平方公式；

（2）请你模仿以上例题分解因式：（a2﹣4a+2）（a2﹣4a+6）+4．

五、解答题(三) (本大题共2小题，每小题12分，共24分)

22.已知，在等边三角形ABC中，点E在AB上，点D在CB的延长线上，且ED＝EC．

（1）【特殊情况，探索结论】

如图1，当点E为AB的中点时，确定线段AE与DB的大小关系，请你直接写出结论：AE　   　DB（填“＞”、“＜”或“＝”）．

（2）【特例启发，解答题目】

如图2，当点E为AB边上任意一点时，确定线段AE与DB的大小关系，请你写出结论，并说明理由．.AE　   　DB（填“＞”、“＜”或“＝”）；理由如下，过点E作EF∥BC，交AC于点F．（请你完成以下解答过程）．

（3）【拓展结论，设计新题】

在等边三角形ABC中，点E在直线AB上，点D在线段CB的延长线上，且ED＝EC，若△ABC的边长为1，AE＝2，求CD的长（直接写出结果）．

23．如图，AM是△ABC的中线，D是线段AM上一点（不与点A重合）．DE∥AB交AC于点F，CE∥AM，连接AE．

（1）如图1，当点D与M重合时，证明△ABD≌△EDC；

（2）如图1，当点D与M重合时，求证：四边形ABDE是平行四边形；

（3）如图2，当点D不与M重合时，（2）中的结论还成立吗？请说明理由．

2022-2023学年度第二学期末教学质量监测

八年级数学科参考答案

一、选择题

1-5   DCCAD     6-10 DBBBA

二、填空题

11.   　2（3+m）（3﹣m）         12. 　12      13.   　　3　     14.    0              

15.    　6　       

三、解答题（一）

16.解：由3x≤x+4得：x≤2，…………………………2分

由﹣2x＜1得：x＞﹣1，…………………………4分

则不等式组的解集为﹣1＜x≤2，…………………………6分

所以该不等式组的非负整数解为0、1、2．…………………………8分

17.解：原式＝，…………………………2分

＝，…………………………4分

＝．…………………………6分

当m＝3时，原式＝．…………………………8分

18解：（1）如图，△A1B1C1、△A2B2C2为所作；…………………………6分

（2）如图，△A1B1C绕P点旋转180°得到△A2B2C2，即旋转中心的坐标为（2，﹣1）．

故答案为：（2，﹣1）．…………………………8分

四、解答题二

19.解：设A客房每间客房的租金为x元，则B客房每间客房的租金为（x﹣30）元．…………………………1分

根据题意，得．…………………………4分

解得x＝240．…………………………6分

经检验，x＝240是原方程的解，且符合题意，…………………………7分

则240﹣30＝210（元）．…………………………8分

答：A客房每间客房的租金为240元，则B客房每间客房的租金为210元．

…………………………9分

20.证明：（1）∵四边形ABCD是平行四边形，

∴AB＝CD，AB∥CD．…………………………1分

∴∠ABF＝∠CDE，…………………………2分

在△ABF和△CDE中，

，

∴△ABF≌△CDE（ASA），…………………………4分

∴AF＝CE；…………………………5分

（2）由（1）可知，△ABF≌△CDE，

∴AF＝CE，∠AFB＝∠CED，…………………………7分

∴AF∥CE，

∴四边形AECF为平行四边形．…………………………9分

21. 解：（1）例题中第二步到第三步运用了因式分解的两数差的完全平方公式，

故答案为：④；…………………………3分

（2）（a2﹣4a+2）（a2﹣4a+6）+4

设a2﹣4a＝x，…………………………4分

原式＝（x+2）（x+6）+4…………………………5分

＝x2+8x+16…………………………6分

＝（x+4）2…………………………7分

＝（a2﹣4a+4）2…………………………8分

＝（a﹣2）4．…………………………9分

五、解答题（三）

22.解：填“=”.………………………3分

（2）填“=”，………………………4分

理由如下，过点E作EF∥BC，交AC于点F，

证明：∵△ABC为等边三角形，

∴△AEF为等边三角形，

∴AE＝EF，BE＝CF， ………………5分

∵ED＝EC，

∴∠D＝∠ECD，

∵∠DEB＝60°﹣∠D，∠ECF＝60°﹣∠ECD，

∴∠DEB＝∠ECF， ………………6分

在△DBE和△EFC中，

，

∴△DBE≌△EFC（SAS）， ………………8分

∴DB＝EF，

则AE＝DB； ………………9分

（3）     3           ………………12分

解析：点E在AB延长线上时，作EF∥AC，则△EFB为等边三角形，

如图所示，同理可得△DBE≌△CFE，

∵AB＝1，AE＝2，

∴BE＝1，

∵DB＝FC＝FB+BC＝2，

则CD＝BC+DB＝3．

23.解：（1）∵DE∥AB，

∴∠EDC＝∠ABM，

∵CE∥AM，

∴∠ECD＝∠ADB，

∵AM是△ABC的中线，且D与M重合，

∴BD＝DC，

∴△ABD≌△EDC， ………………4分

（2）由（1）知△ABD≌△EDC，

∴AB＝ED，

∵AB∥ED，

∴四边形ABDE是平行四边形； ………………7分

（4）  结论成立， ………………8分

理由如下：如图2，过点M作MG∥DE交CE于G，………………9分

∵CE∥AM，

∴四边形DMGE是平行四边形，………………10分

∴ED＝GM，且ED∥GM，

由（1）知，AB＝GM，AB∥GM，

∴AB∥DE，AB＝DE，

∴四边形ABDE是平行四边形.………………12分