新疆乌鲁木齐市第三十六中学2022-2023学年七年级下学期期末数学试题

这是一份新疆乌鲁木齐市第三十六中学2022-2023学年七年级下学期期末数学试题，共16页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

2022-2023学年新疆乌鲁木齐三十六中七年级（下）期末数学试卷
一、选择题（本大题共8小题，每小题3分，共24.0分。在每小题列出的选项中，选出符合题目的一项）
1．下列实数是无理数的是（　　）
A．﹣2 B． C． D．
2．下列事件中适合采用抽样调查的是（　　）
A．对乘坐飞机的乘客进行安检
B．对“天宫2号”零部件的检查
C．学校招聘教师，对应聘人员进行面试
D．对端午节期间市面上粽子质量情况的调查
3．如图，∠1+∠2＝180°，∠3＝108°，则∠4的度数是（　　）

A．72° B．80° C．82° D．108°
4．若x＞y，则下列式子中错误的是（　　）
A．x﹣3＞y﹣3 B．＞ C．x+3＞y+3 D．﹣3x＞﹣3y
5．估计的值在（　　）
A．3和4之间 B．4和5之间 C．5和6之间 D．6和7之间
6．如图，点E在AC的延长线上，下列条件能判断AB∥CD的是（　　）

A．∠1＝∠2 B．∠3＝∠4
C．∠D＝∠DCE D．∠D+∠ACD＝180°
7．为了庆祝中国共产党建党100周年，西山区举行党史知识竞赛，已知竞赛试题共有30道，每一题答对得5分，答错或不答都扣2分．小陈得分要超过100分，则设他答对x道题，则可列不等式正确的是（　　）
A．5x﹣（30﹣x）＞100 B．5x﹣2（30﹣x）＞100
C．5（30﹣x）﹣2x＞100 D．5（30﹣x）﹣x＞100
8．我国古代《算法统宗》里有这样一首诗：“我问开店李三公，众客都来到店中，一房七客多七客，一房九客一房空．”诗中后两句的意思是：如果每一间客房住7人，那么有7人无房住；如果每一间客房住9人，那么就空出一间客房．设该店有客房x间、房客y人，下列方程组中正确的是（　　）
A． B．
C． D．
二、填空题（本大题共6小题，每小题3分，共18.0分）
9．请用不等式表示“x的2倍与3的和大于5”：　 　．
10．已知样本25，21，25，21，23，25，27，29，25，28，30，29，26，24，25，27，26，22，24，25，26，28若组距为2，那么应分为　 　组，在24.5～26.5这一组的频数是　 　．
11．第四象限的点P（x，y）满足|x|＝5，y2＝9，则点P的坐标是　 　
12．某实验学校为了解七年级1200名学生体质健康情况，从中抽取了100名学生进行测试，在这个问题中，样本容量是　 　．
13．若是关于x，y的二元一次方程mx﹣2y＝4的解，则m的值为　 　．
14．如图，将△ABC向右平移得到△DEF，如果BF＝10，CE＝6，则平移的距离是 　 　．

三、解答题（本大题共8小题，共58.0分）
15．计算：﹣12022﹣+|﹣2|．
16．解方程组：．
17．解不等式组．
18．完成下面的证明．
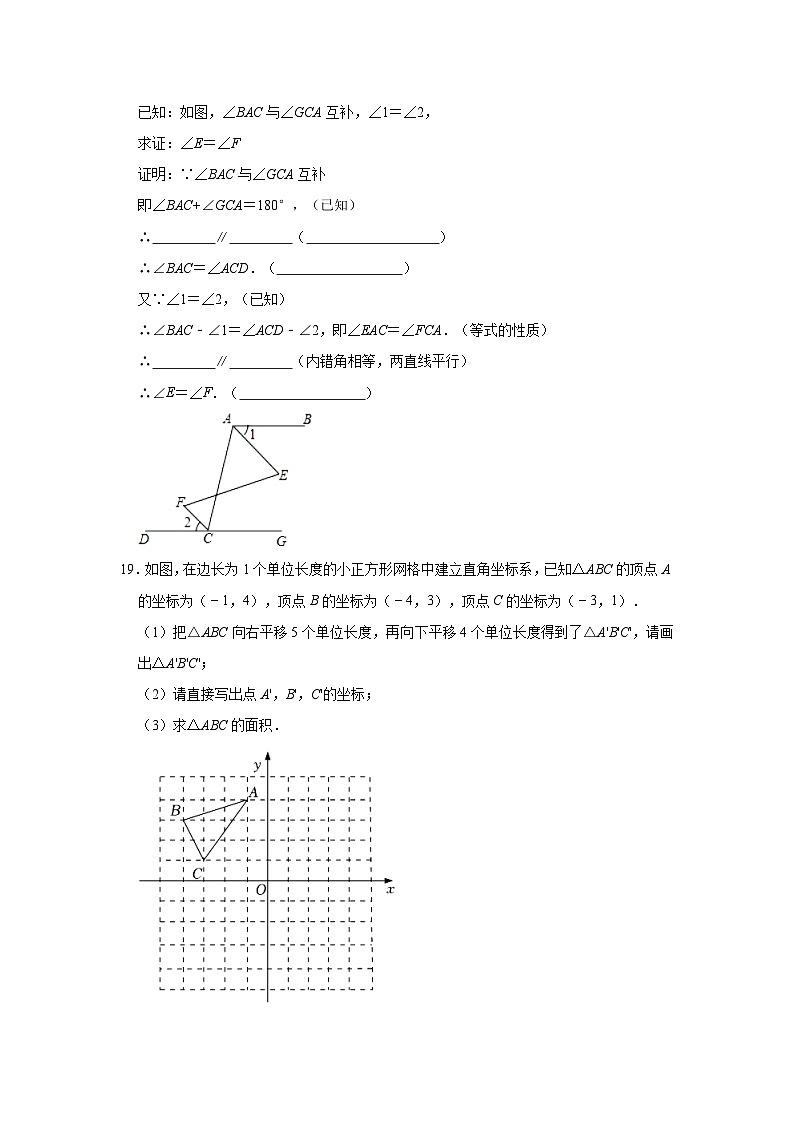
已知：如图，∠BAC与∠GCA互补，∠1＝∠2，
求证：∠E＝∠F
证明：∵∠BAC与∠GCA互补
即∠BAC+∠GCA＝180°，（已知）
∴　 　∥　 　（　 　）
∴∠BAC＝∠ACD．（　 　）
又∵∠1＝∠2，（已知）
∴∠BAC﹣∠1＝∠ACD﹣∠2，即∠EAC＝∠FCA．（等式的性质）
∴　 　∥　 　（内错角相等，两直线平行）
∴∠E＝∠F．（　 　）

19．如图，在边长为1个单位长度的小正方形网格中建立直角坐标系，已知△ABC的顶点A的坐标为（﹣1，4），顶点B的坐标为（﹣4，3），顶点C的坐标为（﹣3，1）．
（1）把△ABC向右平移5个单位长度，再向下平移4个单位长度得到了△A'B'C'，请画出△A'B'C'；
（2）请直接写出点A'，B'，C'的坐标；
（3）求△ABC的面积．

20．学校团委组织志愿者到图书馆整理一批新进的图书．若男生每人整理30本，女生每人整理20本，共能整理680本；若男生每人整理50本，女生每人整理40本，共能整理1240本．求男生、女生志愿者各有多少人？
21．某校数学实践小组就近期人们比较关注的五个话题：“A．5G通讯； B．民法典；C．北斗导航；D．数字经济； E．小康社会”，对某小区居民进行了随机抽样调查，每人只能从中选择一个本人最关注的话题，根据调查结果绘制了如图两幅不完整的统计图．

请结合统计图中的信息，解决下列问题：
（1）数学实践小组在这次活动中，调查的居民共有　 　人；
（2）将上面的最关注话题条形统计图补充完整；
（3）最关注话题扇形统计图中的a＝　 　，话题D所在扇形的圆心角是　 　度；
（4）假设这个小区居民共有10000人，请估计该小区居民中最关注的话题是“民法典”的人数大约有多少？
22．为了预防新冠肺炎疫情的发生，学校免费为师生提供防疫物品．某校花7200元购进洗手液与84消毒液共400瓶，已知洗手液的价格是25元/瓶，84消毒液的价格是15元/瓶．
求：（1）该校购进洗手液和84消毒液各多少瓶？
（2）若购买洗手液和84消毒液共150瓶，总费用不超过2500元，请问最多能购买洗手液多少瓶？


参考答案
一、选择题（本大题共8小题，每小题3分，共24.0分。在每小题列出的选项中，选出符合题目的一项）
1．下列实数是无理数的是（　　）
A．﹣2 B． C． D．
【分析】根据无理数的定义（无理数是指无限不循环小数）逐个判断即可．
解：＝3，
则由无理数的定义可知，属于无理数的是．
故选：D．
【点评】本题考查了无理数，能熟记无理数的定义是解此题的关键，注意：无理数含有①含π的，②开方开不尽的根式，③一些有规律的数，④tan30°．
2．下列事件中适合采用抽样调查的是（　　）
A．对乘坐飞机的乘客进行安检
B．对“天宫2号”零部件的检查
C．学校招聘教师，对应聘人员进行面试
D．对端午节期间市面上粽子质量情况的调查
【分析】由普查得到的调查结果比较准确，但所费人力、物力和时间较多，而抽样调查得到的调查结果比较近似．
解：A、对乘坐飞机的乘客进行安检，意义重大，应采用全面调查，故此选项不合题意；
B、对“天宫2号”零部件的检查，意义重大，应采用全面调查，故此选项不合题意；
C、学校招聘教师，对应聘人员进行面试，人数较少，应采用全面调查，故此选项不合题意；
D、对端午节期间市面上粽子质量情况的调查，数量众多，具有破坏性，应采用抽样调查，故此选项符合题意；
故选：D．
【点评】本题考查了抽样调查和全面调查的区别，选择普查还是抽样调查要根据所要考查的对象的特征灵活选用，一般来说，对于具有破坏性的调查、无法进行普查、普查的意义或价值不大，应选择抽样调查，对于精确度要求高的调查，事关重大的调查往往选用普查．
3．如图，∠1+∠2＝180°，∠3＝108°，则∠4的度数是（　　）

A．72° B．80° C．82° D．108°
【分析】由邻补角定义得到∠2与∠5互补，再由∠1与∠2互补，利用同角的补角相等得到∠1＝∠5，利用同位角相等两直线平行得到a与b平行，利用两直线平行同旁内角互补得到∠6与∠4互补，而∠3与∠6对顶角相等，由∠3的度数求出∠6的度数，进而求出∠4的度数．
解：∵∠1+∠2＝180°，∠2+∠5＝180°，
∴∠1＝∠5，
∴a∥b，
∴∠4+∠6＝180°，
∴∠4＝72°．
故选：A．

【点评】此题考查了平行线的判定与性质，熟练掌握平行线的判定与性质是解本题的关键．
4．若x＞y，则下列式子中错误的是（　　）
A．x﹣3＞y﹣3 B．＞ C．x+3＞y+3 D．﹣3x＞﹣3y
【分析】根据不等式的基本性质，进行判断即可．
解：A、根据不等式的性质1，可得x﹣3＞y﹣3，故A选项正确；
B、根据不等式的性质2，可得＞，故B选项正确；
C、根据不等式的性质1，可得x+3＞y+3，故C选项正确；
D、根据不等式的性质3，可得﹣3x＜﹣3y，故D选项错误；
故选：D．
【点评】本题考查了不等式的性质：
（1）不等式两边加（或减）同一个数（或式子），不等号的方向不变．
（2）不等式两边乘（或除以）同一个正数，不等号的方向不变．
（3）不等式两边乘（或除以）同一个负数，不等号的方向改变．
5．估计的值在（　　）
A．3和4之间 B．4和5之间 C．5和6之间 D．6和7之间
【分析】用“夹逼法”找到在哪两个可化为整数的二次根式之间即可．
解：∵＜＜，
∴4＜＜5，
故选：B．
【点评】考查估算无理数大小的知识；用“夹逼法”估算无理数是常用的估算无理数的方法．
6．如图，点E在AC的延长线上，下列条件能判断AB∥CD的是（　　）

A．∠1＝∠2 B．∠3＝∠4
C．∠D＝∠DCE D．∠D+∠ACD＝180°
【分析】根据平行线的判定定理即可直接作出判断．
解：A．根据内错角相等，两直线平行即可证得AB∥CD；
B．根据内错角相等，两直线平行即可证得BD∥AC，不能证AB∥CD；
C．根据内错角相等，两直线平行即可证得BD∥AC，不能证AB∥CD；
D．根据同旁内角互补，两直线平行，即可证得BD∥AC，不能证AB∥CD．
故选：A．
【点评】本题考查了平行线的判定定理，正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键，不能遇到相等或互补关系的角就误认为具有平行关系，只有同位角相等、内错角相等、同旁内角互补，才能推出两被截直线平行．
7．为了庆祝中国共产党建党100周年，西山区举行党史知识竞赛，已知竞赛试题共有30道，每一题答对得5分，答错或不答都扣2分．小陈得分要超过100分，则设他答对x道题，则可列不等式正确的是（　　）
A．5x﹣（30﹣x）＞100 B．5x﹣2（30﹣x）＞100
C．5（30﹣x）﹣2x＞100 D．5（30﹣x）﹣x＞100
【分析】设他答对x道题，知他答错（30﹣x）题，根据“答对题数×答对数量﹣答错题数×答错扣分＞100”可得答案．
解：设他答对x道题，
根据小陈得分要超过100分可得5x﹣2（30﹣x）＞100，
故选：B．
【点评】本题主要考查由实际问题抽象出一元一次不等式，用不等式表示不等关系时，要抓住题目中的关键词，如“大于（小于）、不超过（不低于）、是正数（负数）”“至少”、“最多”等等，正确选择不等号．因此建立不等式要善于从“关键词”中挖掘其内涵，不同的词里蕴含这不同的不等关系．
8．我国古代《算法统宗》里有这样一首诗：“我问开店李三公，众客都来到店中，一房七客多七客，一房九客一房空．”诗中后两句的意思是：如果每一间客房住7人，那么有7人无房住；如果每一间客房住9人，那么就空出一间客房．设该店有客房x间、房客y人，下列方程组中正确的是（　　）
A． B．
C． D．
【分析】设该店有客房x间，房客y人；根据题意一房七客多七客，一房九客一房空得出方程组即可．
解：设该店有客房x间，房客y人；
根据题意得：，
故选：A．
【点评】本题考查了二元一次方程组的应用；根据题意得出方程组是解决问题的关键．
二、填空题（本大题共6小题，每小题3分，共18.0分）
9．请用不等式表示“x的2倍与3的和大于5”：　2x+3＞5　．
【分析】x的2倍与3的和为2x+3，大于5即＞5，据此列不等式．
解：由题意得，2x+3＞5．
故答案为：2x+3＞5．
【点评】本题考查了由实际问题抽象出一元一次不等式，读懂题意，抓住关键词语，弄清运算的先后顺序和不等关系，才能把文字语言的不等关系转化为用数学符号表示的不等式．
10．已知样本25，21，25，21，23，25，27，29，25，28，30，29，26，24，25，27，26，22，24，25，26，28若组距为2，那么应分为　5　组，在24.5～26.5这一组的频数是　9　．
【分析】根据题意可以求出这组数据的极差，然后根据组距即可确定组数，再根据题目中的数据即可得到在24.5～26.5这一组的频数，本题得以解决．
解：极差是：30﹣21＝9，
∵组距为2，9÷2＝4.5，
∴应分为5组，
在24.5～26.5这一组的频数是：9，
故答案为：5，9．
【点评】本题考查频数分布表，解答本题的关键是明确题意，会求一组数据的极差和划分相应的组数．
11．第四象限的点P（x，y）满足|x|＝5，y2＝9，则点P的坐标是　（5，﹣3）　
【分析】直接利用第四象限内点的坐标特点得出x，y的符号，进而得出答案．
解：∵第四象限内的点P（x，y），
∴x＞0，y＜0，
∵|x|＝5，y2＝9，
∴x＝5，y＝﹣3．
故点P的坐标是：（5，﹣3）．
故答案为：（5，﹣3）．
【点评】此题主要考查了点的坐标以及绝对值和平方根，正确得出x，y的符号是解题关键．
12．某实验学校为了解七年级1200名学生体质健康情况，从中抽取了100名学生进行测试，在这个问题中，样本容量是　100　．
【分析】样本容量则是指样本中个体的数目．
解：了解七年级1200名学生体质健康情况，从中抽取了100名学生进行测试，在这个问题中，样本容量是100，
故答案为：100．
【点评】此题考查了总体、个体、样本、样本容量，解题要分清具体问题中的总体、个体与样本，关键是明确考查的对象．总体、个体与样本的考查对象是相同的，所不同的是范围的大小．样本容量是样本中包含的个体的数目，不能带单位．
13．若是关于x，y的二元一次方程mx﹣2y＝4的解，则m的值为　3　．
【分析】把x与y的值代入方程计算即可求出m的值．
解：把代入方程mx﹣2y＝4中得：2m﹣2＝4，
解得：m＝3．
故答案为：3．
【点评】此题考查了二元一次方程的解，方程的解即为能使方程左右两边相等的未知数的值．
14．如图，将△ABC向右平移得到△DEF，如果BF＝10，CE＝6，则平移的距离是 　2　．

【分析】根据平移的性质可得BE＝CF为平移距离，然后求解即可．
解：∵△ABC沿BC方向向右平移得到△DEF，
∴BE＝CF，
∵BF＝10，EC＝6，
∴BE＝×（10﹣6）＝2，
即平移的距离为2．
故答案为：2．
【点评】本题考查了平移的性质，主要利用了对应顶点的连线的长度等于平移距离．
三、解答题（本大题共8小题，共58.0分）
15．计算：﹣12022﹣+|﹣2|．
【分析】这里，先算﹣12022＝﹣1，＝4，|﹣2|＝2﹣，再进行综合运算．
解：﹣12022﹣+|﹣2|
＝﹣1﹣4+2﹣
＝﹣3﹣．
【点评】本题考查了实数的综合运算，计算过程中要细心，注意正负符号，综合性较强．
16．解方程组：．
【分析】方程组利用加减消元法求出解即可．
解：，
①+②×3得：10x＝50，
解得：x＝5，
把x＝5代入②得：y＝3，
则方程组的解为．
【点评】此题考查了解二元一次方程组，利用了消元的思想，消元的方法有：代入消元法与加减消元法．
17．解不等式组．
【分析】分别求出不等式组中两不等式的解集，找出两解集的公共部分即可．
解：，
由①得：x≥﹣1，
由②得：x＜3，
则不等式组的解集为：﹣1≤x＜3．
【点评】此题考查了解一元一次不等式组，熟练掌握不等式组的解法是解本题的关键．
18．完成下面的证明．
已知：如图，∠BAC与∠GCA互补，∠1＝∠2，
求证：∠E＝∠F
证明：∵∠BAC与∠GCA互补
即∠BAC+∠GCA＝180°，（已知）
∴　AB　∥　DG　（　同旁内角互补，两直线平行　）
∴∠BAC＝∠ACD．（　两直线平行，内错角相等　）
又∵∠1＝∠2，（已知）
∴∠BAC﹣∠1＝∠ACD﹣∠2，即∠EAC＝∠FCA．（等式的性质）
∴　AE　∥　CF　（内错角相等，两直线平行）
∴∠E＝∠F．（　两直线平行，内错角相等　）

【分析】首先判断AB∥CD，然后根据平行线的性质，以及平行线的判定方法证明AE∥CF，根据平行线的性质即可求解．
【解答】证明：∵∠BAC与∠GCA互补
即∠BAC+∠GCA＝180°，（已知）
∴AB∥DG（同旁内角互补，两直线平行）
∴∠BAC＝∠ACD．（两直线平行，内错角相等）
又∵∠1＝∠2，（已知）
∴∠BAC﹣∠1＝∠ACD﹣∠2，即∠EAC＝∠FCA．（等式的性质）
∴AE∥CF（内错角相等，两直线平行）
∴∠E＝∠F．（两直线平行，内错角相等）
故答案为：AB、DG、同旁内角互补，两直线平行、AE、CF、两直线平行，内错角相等．
【点评】本题考查了平行线的性质以及平行线的判定方法，正确证明AE∥CF是关键．
19．如图，在边长为1个单位长度的小正方形网格中建立直角坐标系，已知△ABC的顶点A的坐标为（﹣1，4），顶点B的坐标为（﹣4，3），顶点C的坐标为（﹣3，1）．
（1）把△ABC向右平移5个单位长度，再向下平移4个单位长度得到了△A'B'C'，请画出△A'B'C'；
（2）请直接写出点A'，B'，C'的坐标；
（3）求△ABC的面积．

【分析】（1）利用平移变换的性质分别作出A，B，C的对应点A′，B′，C′即可；
（2）根据图形写出各点的坐标即可；
（3）把三角形的面积看成矩形的面积减去周围的三个三角形面积即可．
解：（1）△A'B'C'如图：

（2）A'（4，0）B'（1，﹣1）C'（2，﹣3）；

（3）△ABC的面积＝正方形面积﹣边上三块小三角形的面积，．
答：△ABC的面积是3.5．

【点评】本题考查作图﹣平移变换，三角形的面积等知识，解题的关键是掌握平移变换的性质，学会用分割法求三角形的面积．
20．学校团委组织志愿者到图书馆整理一批新进的图书．若男生每人整理30本，女生每人整理20本，共能整理680本；若男生每人整理50本，女生每人整理40本，共能整理1240本．求男生、女生志愿者各有多少人？
【分析】设男生志愿者有x人，女生志愿者有y人，根据“若男生每人整理30本，女生每人整理20本，共能整理680本；若男生每人整理50本，女生每人整理40本，共能整理1240本”，即可得出关于x、y的二元一次方程组，解之即可得出结论．
解：设男生志愿者有x人，女生志愿者有y人，
根据题意得：，
解得：．
答：男生志愿者有12人，女生志愿者有16人．
【点评】本题考查了二元一次方程组的应用，找准等量关系，列出二元一次方程组是解题的关键．
21．某校数学实践小组就近期人们比较关注的五个话题：“A．5G通讯； B．民法典；C．北斗导航；D．数字经济； E．小康社会”，对某小区居民进行了随机抽样调查，每人只能从中选择一个本人最关注的话题，根据调查结果绘制了如图两幅不完整的统计图．

请结合统计图中的信息，解决下列问题：
（1）数学实践小组在这次活动中，调查的居民共有　200　人；
（2）将上面的最关注话题条形统计图补充完整；
（3）最关注话题扇形统计图中的a＝　25　，话题D所在扇形的圆心角是　36　度；
（4）假设这个小区居民共有10000人，请估计该小区居民中最关注的话题是“民法典”的人数大约有多少？
【分析】（1）根据选择B的人数和所占的百分比，可以求得本次调查的居民人数；
（2）根据（1）中的结果和统计图中的数据，可以计算出选择A和C的人数，从而可以将条形统计图补充完整；
（3）根据统计图中的数据，可以得到a和话题D所在扇形的圆心角的度数；
（4）根据题意和统计图中的数据，可以计算出计该小区居民中最关注的话题是“民法典”的人数大约有多少．
解：（1）调查的居民共有：60÷30%＝200（人），
故答案为：200；
（2）选择C的居民有：200×15%＝30（人），
选择A的有：200﹣60﹣30﹣20﹣40＝50（人），
补全的条形统计图如右图所示；
（3）a%＝50÷200×100%＝25%，
话题D所在扇形的圆心角是：360°×＝36°，
故答案为：25，36；
（4）10000×30%＝3000（人），
答：该小区居民中最关注的话题是“民法典”的人数大约有3000人．

【点评】本题考查条形统计图、扇形统计图、用样本估计总体，解答本题的关键是明确题意，利用数形结合的思想解答．
22．为了预防新冠肺炎疫情的发生，学校免费为师生提供防疫物品．某校花7200元购进洗手液与84消毒液共400瓶，已知洗手液的价格是25元/瓶，84消毒液的价格是15元/瓶．
求：（1）该校购进洗手液和84消毒液各多少瓶？
（2）若购买洗手液和84消毒液共150瓶，总费用不超过2500元，请问最多能购买洗手液多少瓶？
【分析】（1）设该校购进洗手液x瓶，该校购进84消毒液y瓶，根据“共400瓶；花费7200元”，即可得出关于x，y的二元一次方程组，解之即可得出结论；
（2）设能购买洗手液a瓶，则能购买84消毒液（150﹣a）瓶，根据总费用不超过2500元，列出不等式求解即可．
解：（1）设该校购进洗手液x瓶，该校购进84消毒液y瓶，
依题意有，
解得．
故该校购进洗手液120瓶，该校购进84消毒液280瓶；
（2）设能购买洗手液a瓶，则能购买84消毒液（150﹣a）瓶，
依题意有25a+15（150﹣a）≤2500，
解得a≤25．
故最多能购买洗手液25瓶．
【点评】本题考查了二元一次方程组的应用以及一元一次不等式的应用，解题的关键是：（1）找准等量关系，正确列出二元一次方程组；（2）找准不等关系，正确列出一元一次不等式．