2023年河南省商丘市柘城县中考二模数学试题（含解析）

这是一份2023年河南省商丘市柘城县中考二模数学试题（含解析），共24页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

2023年河南省商丘市柘城县中考二模数学试题
学校:___________姓名：___________班级：___________考号：___________

一、单选题
1．的相反数是（    ）
A． B．6 C． D．
2．运营商和互联网大数据显示，线下消费成为2023年春节消费最亮增长点，春节期间商圈接待量达亿人次，比去年增长，其中数据“亿”用科学记数法表示为（    ）
A． B． C． D．
3．下列调查中适合全面调查的是（    ）
A．对某品牌灯泡的使用寿命的调查 B．对黄河流域中的生物多样性情况的调查
C．对某市中学生的睡眠情况的调查 D．对神舟十四号载人飞船发射前的零部件的检查
4．如图，是由9个大小相同的小正方体搭成的几何体，其左视图是（    ）
  
A．   B．   C．   D．  
5．下列运算正确的是（    ）
A． B． C． D．
6．一元二次方程的根的情况是（    ）
A．有两个不相等的实数根 B．没有实数根 C．有两个相等的实数根 D．只有一个实数根
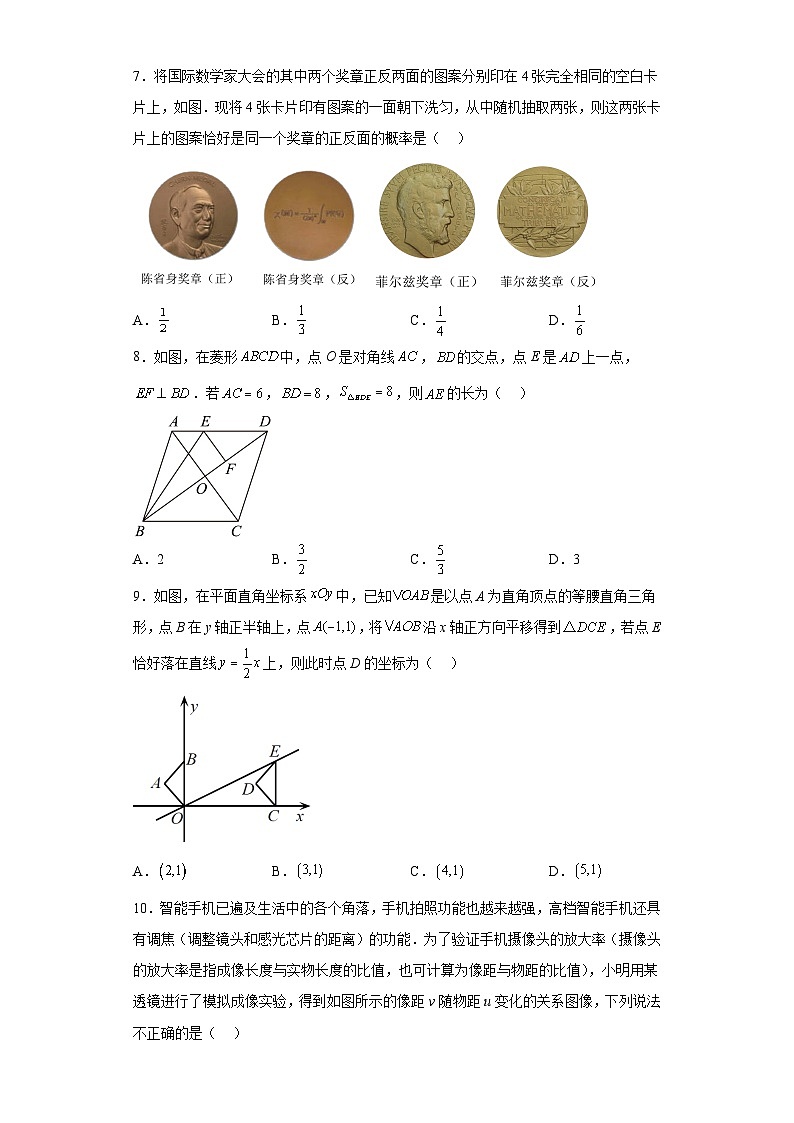
7．将国际数学家大会的其中两个奖章正反两面的图案分别印在4张完全相同的空白卡片上，如图．现将4张卡片印有图案的一面朝下洗匀，从中随机抽取两张，则这两张卡片上的图案恰好是同一个奖章的正反面的概率是（    ）
        
A． B． C． D．
8．如图，在菱形中，点O是对角线，的交点，点E是上一点，．若，，，则的长为（    ）
  
A．2 B． C． D．3
9．如图，在平面直角坐标系中，已知是以点A为直角顶点的等腰直角三角形，点B在y轴正半轴上，点，将沿x轴正方向平移得到，若点E恰好落在直线上，则此时点D的坐标为（    ）
  
A． B． C． D．
10．智能手机已遍及生活中的各个角落，手机拍照功能也越来越强，高档智能手机还具有调焦（调整镜头和感光芯片的距离）的功能．为了验证手机摄像头的放大率（摄像头的放大率是指成像长度与实物长度的比值，也可计算为像距与物距的比值），小明用某透镜进行了模拟成像实验，得到如图所示的像距v随物距u变化的关系图像，下列说法不正确的是（    ）
  
A．当物距为时，像距为 B．当像距为时，透镜的放大率为2
C．物距越大，像距越小 D．当透镜的放大率为1时，物距和像距均为

二、填空题
11．若二次根式有意义，则实数x的取值范围是_________．
12．请写出一个图像经过y轴正半轴的函数的解析式_________．
13．一把直尺和一个含角的直角三角板按如图所示方式摆放，其中三角板的一个顶点落在直尺上．若，则_________．
  
14．如图，在扇形中，，点C，D分别是和上的点，且，将扇形沿翻折，翻折后的恰好经过点O．若，则图中阴影部分的面积是_________．
  
15．如图，已知正方形的边长为4，点E是边的中点，连接，，将绕点E旋转得到线段，连接，当时，的长为_________．
  

三、解答题
16．（1）计算：．
（2）解二元一次方程组：．
17．《中共中央国务院关于做好2023年全面推进乡村振兴重点工作的意见》指出：实施玉米单产提升工程．为了加快玉米生物育种产业化步伐，某省农科院选择10个试验点乡镇，每个乡镇选择两块自然条件相近的试验田分别种植培育A，B两种玉米种子，得到的亩产量数据如下（单位：）：
A种玉米：1004 1019 1018 1002 1006 1011 1018 1011 1003 1016
B种玉米：1007 1004 1011 1010 1002 1012 1006 1014 1004 1009
整理以上数据，并绘制如图所示的折线统计图．

根据以上信息，回答下列问题：
(1)A种玉米亩产量的中位数为_________，B种玉米亩产量的中位数为_________．
(2)观察折线统计图，从玉米的亩产量或亩产量的稳定性的角度分析，你认为农科院应推荐种植哪种玉米？并说明理由．
18．如图，的顶点O与坐标原点重合，边在x轴正半轴上，，，反比例函数的图像经过顶点C，与边交于点D．
  
(1)求反比例函数的表达式．
(2)尺规作图：作的平分线交x轴于点E．（保留作图痕迹，不写作法）
(3)在（2）的条件下，连接，若，求证：．
19．无影塔位于河南汝南城南，俗传夏至正午无塔影，故称无影塔．某数学兴趣小组在学习完锐角三角函数后，分成A，B两个小组利用无人机测量无影塔的高度．如下是两个小组设计的两种测量方案．
课题
测量无影塔的高度
方案
A组方案
B组方案
测量示意图
  
  
方案说明
点A为塔的最高点，点B为塔底座的最右端，无人机在点C处测得塔顶端A处的俯角为，测得点B处的俯角为（A，B，C三点在同一竖直平面内）
点A为塔的最高点，点B，C在同一水平线上，在点B处测得塔顶端A处的俯角为，在点C处测得塔顶端A处的俯角为（A，B，C三点在同一竖直平面内）
测量数据
，，无人机距离塔底端所在水平地面的距离为36m
，，点B，C之间的距离为28m，无人机距离塔底端所在水平地面的距离为38m
参考数据
，，，
，，
(1)他们在计算过程中发现A组的方案比B组的方案误差大，为什么？
(2)请利用B组的方案求该塔的高度．
20．某学校为做好绿化、改善育人环境，准备购买两种树苗在学校栽种．已知1棵种树苗比1棵种树苗贵5元，用400元购买的种树苗与用300元购买的种树苗的数量相同．
(1)求购买1棵种树苗和1棵种树苗各需多少元；
(2)若该校计划购买两种树苗共150棵，且种树苗的数量不少于种树苗的一半，则怎样购买可以使购买费用最低，最低费用为多少？
21．如图，是一个抛物线形拱桥的截面图，在正常水位时，水位线与拱桥最高点的距离为，水面宽．

(1)请你建立合适的平面直角坐标系，并根据建立的平面直角坐标系求出该抛物线的解析式．
(2)已知一艘船（可近似看成长方体）在此航行时露出水面的高度为，若这艘船的宽度为，当水位线比正常水位线高出时，这艘船能否从该抛物线形拱桥下方顺利通过，请说明理由．
22．综合与探究
我们知道：顶点在圆上，并且两边都和圆相交的角叫做圆周角，一条弧所对的圆周角的度数等于它所对的圆心角度数的一半．类似地，我们定义：顶点在圆外，并且两边都和圆相交的角叫做圆外角．
【探究】
圆外角的度数与它所夹的弧所对的圆心角的度数之间有什么关系？
【实验】
（1）如图1，当圆外角的两条边分别与有两个公共点时，改变的度数，测量得到如下数据：
的度数




所对的圆心角度数（）




所对的圆心角度数（）




猜想：_________．（用含，的式子表示）
  
【特例】
（2）当圆外角的其中一条边与只有一个公共点时，如图2，射线与相切于点A，射线经过圆心O，交于另一点C，设，所对的圆心角度数分别为，，写出的度数与，之间的数量关系，并证明．
【应用】
（3）在（2）的条件下，连接，若，，求的半径．
23．综合与实践
在一节数学课上，张老师提出了这样一个问题：如图1，在等腰直角三角形中，，D是边上一动点（不与点B重合），，，交于点F．猜想线段，之间的数量关系并说明理由．

小聪与同桌小明讨论后，仍不得其解，张老师给出提示：“数学中常通过把一个问题特殊化来找到解题思路．”两人茅塞顿开，于是进行了如下讨论，请仔细阅读，并完成相应的任务．
小聪：已知点D是动点，因此可以将点D移动到一个特殊的位置．当点D与点C重合时，如图2所示．此时可以分别延长，交于点H，如图3所示，可知是等腰三角形，证明，从而得出线段，之间的数量关系．

小明：对于图2，我有不同的证明方法，过点F分别作的平行线，交边于点M，N，如图4所示，可知，且，又∵，可得与的相似比为，从而得出线段之间的数量关系．
任务一：如图2，猜想线段之间的数量关系为_________．
任务二：通过阅读上述讨论，请在小聪与小明的方法中选择一种，就图1中的情形判断线段之间的数量关系，并给出证明．
任务三：若，其他条件不变，当是直角三角形时，直接写出的长．

参考答案：
1．C
【分析】相反数的概念：只有符号不同的两个数叫做互为相反数．
【详解】解：根据相反数的概念，可知的相反数是，
故选：C．
【点睛】本题考查了相反数，掌握相反数的定义是解答本题的关键．
2．B
【分析】科学记数法的表示形式为的形式，其中，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．
【详解】解：数据“亿”用科学记数法表示为．
故选：B．
【点睛】此题考查科学记数法的表示方法．科学记数法的表示形式为的形式，其中，n为整数，表示时关键要正确确定a的值以及n的值．
3．D
【分析】根据抽样调查与全面调查的特点依次判断即可．
【详解】解：选项A中，对某品牌灯泡的使用寿命的调查，调查具有破坏性，适合抽样调查，不符合题意；
选项B中，对黄河流域中的生物多样性情况的调查，调查范围广，工作量大，且不可能做到全面调查，适合抽样调查，不符合题意；
选项C中，对某市中学生的睡眠情况的调查，调查范围广，工作量大，适合抽样调查，不符合题意；
选项D中，对神舟十四号载人飞船发射前的零部件的检查，事关重大，适合全面调查，符合题意；
故选D．
【点睛】题目主要考查抽样调查与全面调查的特点，熟练掌握全面调查与抽样调查的特点是解题关键．
4．A
【分析】根据左视图是从左边看到的图形进行解答．
【详解】解：根据左视图的概念，从左向右看，该几何体有列，第列有层，第列有层，第列有层．
故选A．
【点睛】本题考查了三视图的概念，左视图即从左往右看得到的图形．
5．B
【分析】根据合并同类项，同底数幂的乘法，积的乘方，完全平方公式的运算法则计算各项，即可得到答案．
【详解】解：A．与不是同类项，不能进行合并，故选项A错误；
B．，故B选项正确；
C．．故C选项错误；
D．，故D选项错误，
故选：B．
【点睛】本题考查了合并同类项，同底数幂的乘法，积的乘方，完全平方公式，熟练掌握运算法则是解题的关键．
6．A
【分析】根据根的判别式进行解答即可．
【详解】解：由题意，可知，
∴该一元二次方程有两个不相等的实数根，
故选：A．
【点睛】本题考查了一元二次方程 (为常数)的根的判别式，理解根的判别式对应的根的三种情况是解题的关键．当时，方程有两个不相等的实数根；当时，方程有两个相等的实数根；当时，方程没有实数根．
7．B
【分析】先画出树状图，然后根据概率公式进行计算即可．
【详解】解：将陈省身奖章（正）（反）分别记为，，将菲尔兹奖章（正）（反）分别记为、．由题意，可画树状图如下：
  
由树状图可知，共有12种等可能的结果，其中抽取的两张卡片上的图案恰好是同一个奖章的正反面的结果有4种，
∴P（这两张卡片上的图案恰好是同一个奖章的正反面），故B正确．
故选：B．
【点睛】本题主要考查了列表法或画树状图法求概率，解题的关键是根据题意画出树状图或列出表格．
8．C
【分析】根据可以求出的长，结合菱形的性质可求出边长，根据平行线分线段成比例，即可求解．
【详解】解：∵，，
∴，
∴，
∵四边形ABCD为菱形，AC＝6，
∴，，，
∴，
∵，
∴，
∴，即，解得，
∴，
故选C．
【点睛】本题考查了菱形的性质，平行线分线段成比例，灵活运用所学知识是解题关键．
9．B
【分析】根据点，求出点B的坐标，再结合即可求出点E的坐标，从而知道平移的方向，即可求解．
【详解】解：∵点，
∴，
∵是以点A为直角顶点的等腰直角三角形，
∴，
∴，
∵E是点B沿x轴向右平移得到的点，
∴点E的纵坐标为2，
将代入中，得，
∴点，
∴点E是点B向右平移4个单位长度得到的，
∴点D也是点A向右平移4个单位长度得到的，
∴点，即点，
故选：B．
【点睛】本题考查了平移的性质，等腰直角三角形的性质，求出平移的方向是解题关键．
10．B
【详解】解：由函数图象可知：当物距为时，像距为，故选项A说法正确；
由函数图象可知：当像距为时，物距为，放大率为，故选项B说法错误；
由函数图象可知：物距越大，像距越小，故选项C说法正确；
由题意可知：当透镜的放大率为1时，物距和像距均为，故选项D说法正确，
故选：B．
【点睛】本题考查了函数图象的分析，理解题意，认真分析函数图象是解决本题的关键．
11．
【分析】根据二次根式有意义的条件（被开方式大于等于0）计算即可．
【详解】解：若使二次根式有意义，
则，
解得．
故答案为：
【点睛】本题考查了二次根式有意义的条件，熟记二次根式的定义是解题关键．
12．（答案不唯一）
【分析】由各函数的图像与性质可得答案．
【详解】解：由题意，经过y轴正半轴的函数的解析式可以为，
故答案为：（答案不唯一）．
【点睛】本题考查的是函数的性质，熟记各函数的图像是解本题的关键．
13．/122度
【分析】由平行线的性质得到，再利用三角形的内角和定理即可求解．
【详解】解：在图中标记，如图所示．
  
∵直尺的对边平行，
∴．
∴．
故答案为：．
【点睛】本题考查了三角形内角和定理，平行线的性质，掌握“两直线平行，同位角相等”是解题的关键．
14．
【详解】过点O作交于点E，连接OC，CE，由折叠的性质结合所作辅助线可得出为等边三角形，即．再根据平行线的性质可求出，从而可求出，进而可求出，利用锐角三角函数可求出，最后根据，结合扇形面积公式和三角形面积公式求解即可．
【分析】解：过点O作交于点E，连接，如图，
  
∴，
∴为等边三角形，
∴．
∵，，
∴．
∵，
∴，
∴，
∴，
∴．
故答案为：．
【点睛】本题考查折叠的性质，扇形的面积公式，平行线的性质，等边三角形的判定与性质，解直角三角形等知识．正确作出辅助线并利用数形结合的思想是解题关键．
15．或
【分析】本题分两种情况：①点F在左侧，②点F在右侧，讨论即可．
【详解】∵正方形的边长为4，点E是边BC的中点，
∴．
在中，由勾股定理，得．
在中，由勾股定理，得．
由旋转的性质，可知，
∴．
由题意，可知需分以下两种情况讨论．
①当点F在左侧时，
过点F作交的延长线于点G，如解图1所示，
  
则．
∵，
∴．
∵，
∴．
∴，．
∴．
∴在中，由勾股定理，得．
②当点F在右侧时，
过点F作交的延长线于点G，如图2所示．
  
同①，可知．
∴，．
∴．
∴在中，由勾股定理，得．
综上所述，当时，的长为或．
【点睛】本题考查了正方形的性质，旋转的性质，勾股定理，全等三角形的判定与性质等知识．明确题意，添加合适辅助线，找出所求问题需要的条件是解题的关键．
16．（1）；（2）
【分析】（1）利用绝对值的意义，零指数幂的定义，以及实数的运算法则求解；
（2）利用加减消元法或代入消元法求解即可．
【详解】解：（1）原式．
（2），得．
，得，解得．
将代入中，得，解得．
该二元一次方程组的解为．
【点睛】本题考查了零指数幂的运算，绝对值的运算，实数的运算法则，解二元一次方程组，熟练掌握相关运算法则是解题的关键．
17．(1)，
(2)所以从玉米的亩产量来看，应该推荐种植A种玉米．从亩产量的稳定性来看，应该推荐种植B种玉米，理由见解析

【分析】（1）根据中位数的定义求解即可；
（2）A的产量高，但是波动大，B的产量低，但是波动小，据此求解即可.
【详解】（1）解：分别把两种玉米的产量从低到高排列为：
A种玉米：1002  1003  1004  1006  1011  1011  1016  1018  1018  1019
B种玉米：1002  1004  1004  1006  1007  1009  1010  1011  1012  1014
∴A种玉米亩产量的中位数为，B种玉米亩产量的中位数为，
故答案为：，；
（2）解：观察折线统计图，可知A种玉米的亩产量较高．B种玉米的亩产量比较稳定，所以从玉米的亩产量来看，应该推荐种植A种玉米．从亩产量的稳定性来看，应该推荐种植B种玉米．
【点睛】本题主要考查了求中位线，折线统计图，方差的含义，灵活运用所学知识是解题的关键．
18．(1)
(2)见解析
(3)见解析

【分析】（1）点C作于点F，解求出，的长度，从而求出点C的坐标，然后代入反比例函数解析式即可求解；
（2）根据角平分线的作图方法作图即可；
（3）利用平行线的性质，角平分线的定义可求，进而求出，利用三角形内角和定理可求出，然后利用等腰三角形的判定即可求解．
【详解】（1）解：过点C作于点F，如解图所示．
  
在中，，，
∴，．
∴．
把代入反比例函数中，得．
∴反比例函数的表达式为．
（2）解：如解图所示，所作射线即为所求．
  
（3）证明：在中，，．
∵，
∴．
∵平分，
∴．
∵，
∴．
∴．
∴．
∴．
∴．
【点睛】本题考查了反比例函数的图象与性质，尺规作图（角平分线），平行四边形的性质等知识．明确题意，找出所求问题需要的条件是解题的关键．
19．(1)见解析
(2)26m

【分析】（1）由A组的方案测得塔底端的俯角不是塔底正中心的，可得误差大的原因；
（2）记塔底端中心为点D，连接并延长交于点E，如解图所示，则，．设．可得．可得．从而可得．
【详解】（1）解： A组的方案测得塔底端的俯角不是塔底正中心的，故A组方案的误差较大．
（2）记塔底端中心为点D，连接并延长交于点E，如解图所示，则，．
  
设．
在中，∵，
∴．
在中，∵，
∴．
∴，
解得．
∴．
答：该塔的高度约为26m．
【点睛】本题考查的是解直角三角形的应用，掌握仰角俯角的含义是解本题的关键．
20．(1)购买1棵种树苗需要20元，购买1棵种树苗需要15元
(2)当购买种树苗50棵，购买种树苗100棵时，购买费用最低，最低费用为2500元

【分析】（1）设1棵种树苗元，则1棵种树苗元，根据用400元购买的种树苗与用300元购买的种树苗的数量相同，列出分式方程求解即可；
（2）设购买种树苗棵，则购买种树苗棵，购买费用为元，先求出的取值范围，再列出关于的一次函数的解析式，取最小值即可得到结果．
【详解】（1）解：设1棵种树苗元，则1棵种树苗元，
由题意得，，
解得，，
经检验是原方程的解，且符合题意，
，
答：购买1棵种树苗需要20元，购买1棵种树苗需要15元；
（2）解：设购买种树苗棵，则购买种树苗棵，购买费用为元，
种树苗的数量不少于种树苗的一半，
，
，
由题意得，，
，
随的增大而增大，
当时，去的最小值，最小值为，
此时，，
答：当购买种树苗50棵，购买种树苗100棵时，购买费用最低，最低费用为2500元．
【点睛】本题主要卡超了分式方程的应用，一次函数的应用，一元一次不等式的应用，读懂题意，找出等量或不等关系是解题的关键．
21．(1)抛物线的解析式为（答案不唯一，建立的平面直角坐标系不同则答案不同）
(2)这艘船能从该抛物线形拱桥下方顺利通过，理由见解析

【分析】（1）根据拱桥的实际问题建立直角坐标系，再根据建立直角坐标系得到抛物线的解析式即可解答；
（2）根据题意得到船的最高点的纵坐标为，再根据抛物线的解析式为得到，进而得到这艘船最高点在同一水平面的拱桥的宽度为即可解答．
【详解】（1）解：建立的平面直角坐标系如解图所示．

观察图象，可知该抛物线的顶点为，点．
∴可设该抛物线的解析式为．
将点代入中，得，
解得．
∴该抛物线的解析式为；
（答案不唯一，建立的平面直角坐标系不同则答案不同）；
（2）解：能，理由如下：
当水位线比正常水位线高出时，此时船的最高点的纵坐标为．
将代入中，
解得，
∴此时与这艘船最高点在同一水平面的拱桥的宽度为（）．
∵，
∴这艘船能从该抛物线形拱桥下方顺利通过．
【点睛】本题考查了二次函数与实际问题，掌握二次函数的性质是解题的关键．
22．（1）（2），证明见解析（3）
【分析】（1）通过分析表格中数据间的数量关系即可得出猜想；
（2）连接，根据切线的性质推出，再由，即可推出；
（3）过点C作于点D，根据，设，，再证明得出，求出，最后利用勾股定理即可求出圆的半径．
【详解】（1）根据表中数据可猜想，
故答案是：．
（2），证明如下：
连接，如图所示，
∵与相切于点A，
∴．
∴，即．
∵，即，
∴．
∴．
  
（3）过点C作于点D，如图所示．
∵，
可设，．
∴，．
∴．
∵，，
∴．
∴，即，
解得，．
在中，由勾股定理，得，
即，  
解得（负值已舍去）．
∴．
的半径为．
【点睛】本题主要考查了切线的性质，相似三角形的判定与性质，勾股定理等知识，熟练掌握切线的性质，相似三角形的判定与性质是解题的关键．
23．任务一：，任务二：，证明见解析，任务三：或
【分析】任务一：根据小聪与小明的提示猜想即可；任务二：选择其中一个同学的方法，根据提示证明即可；任务三：分类讨论直角三角形的直角顶点，当时或当时，分别计算即可；
【详解】解：任务一：．
任务二：选择小明的方法：．
证明：过点F分别作的平行线，交于点M，N，如解图1所示．

∵是等腰直角三角形，，
∴．
∵，
∴，．
∴．
∵，
∴，
∴．
∵，
∴．
∵，
∴．
∴，即．
∴．
∴．
∴，．
∵，即，
∴．
∴，
∴．
∴．
任务三：或．
①当时，点D与点C重合，如图2所示．

是等腰直角三角形，，
．
当时，如图3所示．

∵是等腰直角三角形，，
∴．
∵，，
∴．
∴．
∴．
∴．
∴．
综上所述，的长为或．
【点睛】本题考查了等腰三角形的性质与判定、相似三角形的性质与判定等知识点，辅助线的添加是解题关键．