2023年广东省佛山外国语学校中考数学三模试题（含解析）

这是一份2023年广东省佛山外国语学校中考数学三模试题（含解析），共22页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
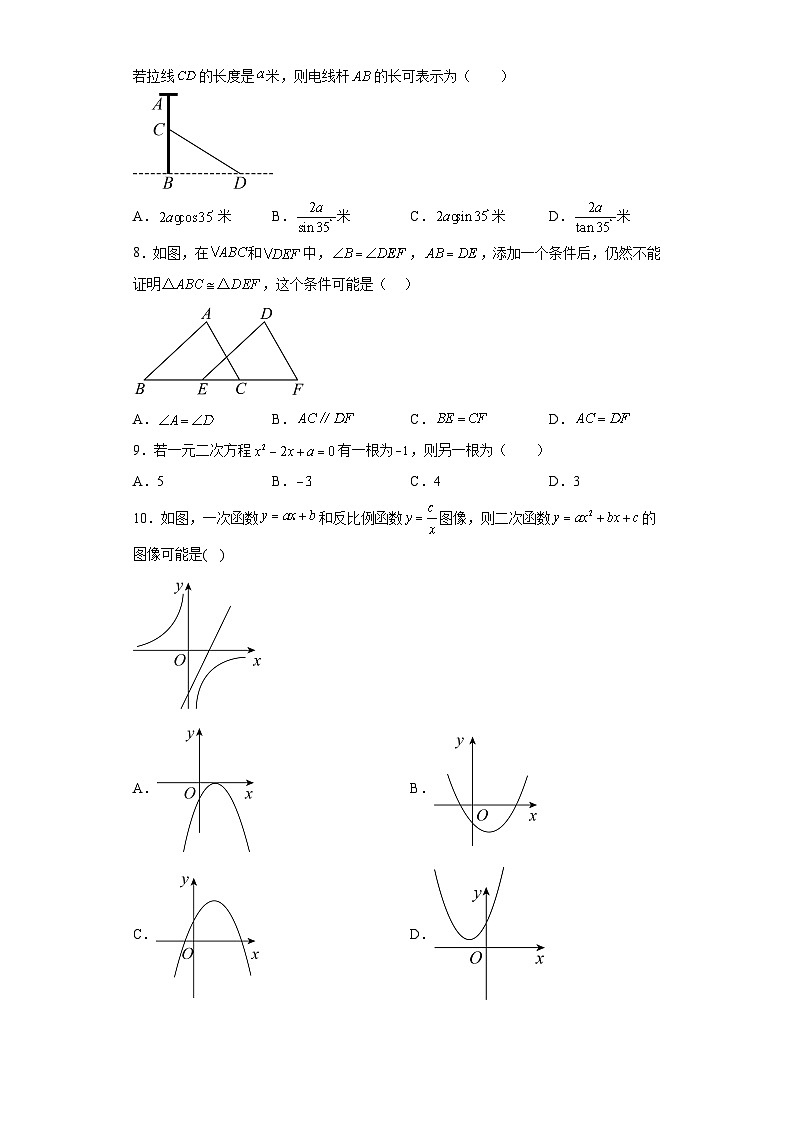
2023年广东省佛山外国语学校中考数学三模试题学校:___________姓名：___________班级：___________考号：___________ 一、单选题1．据旅游部官网消息，2023年春节7天假日，全国国内出游约308000000人次．数据308000000用科学记数法表示为（    ）A． B． C． D．2．如图，直线c与直线a、b都相交．若，，则（　　）A． B． C． D．3．一个不透明的袋子中装有20个小球，其中12个红球，8个绿球，这些小球除颜色外完全相同．从袋子中随机摸出一个小球，则摸出的小球是红球的概率是（    ）A． B． C． D．4．下列运算中，正确的是（    ）A． B．C． D．5．如图，四边形内接于，连接，，若，则（    ）A． B． C． D．6．将向上平移2个单位后所得的抛物线的解析式为（    ）A． B． C． D．7．如图，电线杆的中点处有一标志物，在地面点处测得标志物的仰角为35°，若拉线的长度是米，则电线杆的长可表示为（　　）A．米 B．米 C．米 D．米8．如图，在和中，，，添加一个条件后，仍然不能证明，这个条件可能是（    ）A． B． C． D．9．若一元二次方程有一根为，则另一根为（　　）A．5 B． C．4 D．310．如图，一次函数和反比例函数图像，则二次函数的图像可能是(   )  A．   B．  C．   D．   二、填空题11．若代数式有意义，则实数x的取值范围是 _____．12．点关于轴的对称点是_____．13．已知一根弹簧在不挂重物时长6cm，在一定的弹性限度内，每挂1kg重物弹簧伸长0.3cm. 则该弹簧总长y(cm)随所挂物体质量x(kg)变化的函数关系式为__________.14．一个多边形的每一个外角都等于，则这个多边形的内角和为_________°．15．一个圆锥的侧面积为，底面圆半径为2，则该圆锥的母线长为______．16．如图，在直角坐标系中，点A的坐标是，点B是x轴上的一个动点，将线段绕点A逆时针旋转至点C，连接．在运动过程中，的最小值为______． 三、解答题17．解不等式组：并在数轴上表示它的解集．18．先化简，再求值：，其中19．某校为调查学生对海洋科普知识的了解情况，从全校学生中随机抽取名学生进行测试，测试成绩进行整理后分成五组，并绘制成如下的频数直方图和扇形统计图．请根据图中信息解答下列问题：（1）补全频数直方图；（2）在扇形统计图中，“70~80”这组的百分比__________；（3）已知“80~90”这组的数据如下：81，83，84，85，85，86，86，86，87，88，88，89．抽取的名学生测试成绩的中位数是__________分；（4）若成绩达到80分以上（含80分）为优秀，请你估计全校1200名学生对海洋科普知识了解情况为优秀的学生人数．20．如图，在中，，是中点，连接．分别过点，点作，，交点为．  (1)求证：四边形是菱形；(2)若，，求四边形的面积．21．如图，一次函数的图象与y轴交于点A，与反比例函数的图象交于点和点，连接．(1)求的值；(2)求的面积．22．某家电销售商城电冰箱的销售价为每台2100元，空调的销售价为每台1750元，每台电冰箱的进价比每台空调的进价多400元，商城用80000元购进电冰箱的数量与用64000元购进空调的数量相等．(1)求每台电冰箱与空调的进价分别是多少？(2)现在商城准备一次购进这两种家电共100台，设购买电冰箱x台，这100台家电的销售总利润为y元，要求购进空调数量不超过电冰箱数量的2倍，总利润不低于13000元，请分析合理的方案共有多少种？并确定获利最大的方案以及最大利润．23．如图，为的两条半径，直线l与相切于点B．(1)请用无刻度的直尺和圆规过点O作线段的垂线（要求：不写作法，保留作图痕迹）；(2)连接，若（1）中所作垂线分别与，直线l交于点C和点D．①求证：；②若的半径为4，，求的长．24．如图，抛物线与x轴交于两点，与y轴交于点C，抛物线的对称轴交x轴于点D，已知．(1)求抛物线的函数表达式；(2)点E是线段上的一个动点，过点E作x轴的垂线与抛物线相交于点F，当点E运动到什么位置时，四边形的面积最大?求出四边形的最大面积及此时E点的坐标；(3)在y轴上是否存在点P，使得？若存在，请直接写出P点的坐标，若不存在，请说明理由．
参考答案：1．A【分析】绝对值大于1的数可以用科学记数法表示，一般形式为，为正整数，且比原数的整数位数少1，据此可以解答．【详解】解：数据308000000用科学记数法表示为．故选：A．【点睛】本题考查用科学记数法表示较大的数，熟练掌握科学记数法表示较大的数一般形式为，其中，是正整数，正确确定的值和的值是解题的关键．2．A【分析】根据对顶角相等，得出，根据两直线平行，同位角相等，得出．【详解】解：如图，∵，和是对顶角，∴，∵，∴，故A正确．故选：A．【点睛】本题主要考查了平行线的性质，对顶角性质，解题的关键是熟练掌握：两直线平行，同位角相等；两直线平行，内错角相等；两直线平行，同旁内角互补．3．D【分析】根据概率的求法，找准两点：①全部情况的总数；②符合条件的情况数目；二者的比值就是其发生的概率．【详解】解：不透明的袋子中装有20个小球，其中12个红球、8个绿球，袋子中随机摸出一个小球，则摸出的小球是红球的概率为．故选：D．【点睛】本题考查了概率的求法：如果一个事件有n种可能，而且这些事件的可能性相同，其中事件A出现m种结果，那么事件A的概率，掌握概率的求解方法是解题的关键．4．C【分析】直接利用幂的乘方、积的乘方运算法则、平方差公式以及同底数幂乘除法运算法则分别计算得出答案即可．【详解】解：A、，故此选项不符合题意；B、，故此选项不符合题意；C、，故此选项符合题意；D、，故此选项不符合题意；故选：C．【点睛】本题主要考查了积幂的乘方、积的乘方运算、平方差公式以及同底数幂乘除法，正确掌握相关运算法则是解题的关键．5．A【分析】连接，证明，得出，则，再根据圆内接四边形对角互补，即可求解．【详解】解：连接，在和中，，∴，∵，，∴，∴，∵四边形内接于，∴，故选：A．  【点睛】本题主要考查了圆内接四边形，解题的关键是掌握圆的内接四边形对角互补．6．A【详解】解：根据函数图像平移法则：“上加下减”得：抛物线向上平移2个单位得到抛物线的解析式为．故选：A．7．C【分析】先根据锐角三角函数的定义求出的长，然后根据中点的定义可得出结论．【详解】解：∵，∴，∵点C是的中点，∴．故选：C．【点睛】本题考查的是解直角三角形的应用—仰角俯角问题，解答此题的关键是熟记锐角三角函数的定义．8．D【分析】根据全等三角形的判定，利用、、即可得出答案．【详解】解：∵，，∴当时，由可得，故A不符合题意；当时，则，由可得，故B不符合题意；当时，则，由可得，故C不符合题意；当时，不能得出，故D符合题意；故选：D．【点睛】本题主要考查全等三角形的判定，解答的关键是熟记全等三角形的判定条件并灵活运用．9．D【分析】将代入方程即可求出a的值．【详解】解：将代入方程可得：，∴，∴方程为，∴，解得，，故选：D．【点睛】本题考查一元二次方程的解，解一元二次方程，关键是掌握能使一元二次方程左右两边相等的未知数的值是一元二次方程的解．10．B【分析】根据一次函数与反比例函数的图象位置，确定出的正负，进而利用二次函数图象与性质判断即可．【详解】解：观察图象可得：，二次函数图象开口向上，对称轴在轴右侧，与轴交点在负半轴，则二次函数的图象可能是  ，故选：B．【点睛】本题主要考查了反比例函数的图象，一次函数图象，以及二次函数的图象，熟练掌握各自图象的性质是解本题的关键．11．【分析】根据二次根式的被开方数是非负数即可得出答案．【详解】解：∵，∴．故答案为：．【点睛】本题考查了二次根式有意义的条件，掌握二次根式的被开方数是非负数是解题的关键．12．(-2，-3)【分析】点(x，y)关于y轴的对称点的坐标是(-x，y)，据此进行求解即可得.【详解】点P(2，-3)关于y轴的对称点坐标是(-2，-3)，故答案为(-2，-3).【点睛】本题考查了关于y轴对称的点的坐标，解决的关键是对知识点的正确记忆．关于横轴的对称点，横坐标不变，纵坐标变成相反数；关于纵轴的对称点，纵坐标不变，横坐标变成相反数；关于原点的对称点，横纵坐标都变成相反数．13．y=0.3x+6【分析】弹簧总长=挂上xkg的重物时弹簧伸长的长度+弹簧原来的长度，把相关数值代入即可【详解】解：∵每挂1kg重物弹簧伸长0.3cm，∴挂上x kg的物体后，弹簧伸长0.3x cm，∴弹簧总长y=0.3x+6．故答案为：y=0.3x+6．【点睛】本题考查了根据实际问题列一次函数关系式；得到弹簧总长的等量关系是解决本题的关键．14．720【分析】由多边形外角的性质可求解多边形的边数，再利用多边形的内角和定理可求解．【详解】解：，．即这个多边形的内角和是．故答案为：．【点睛】本题主要考查多边形的内角与外角，求解多边形的边数是解题的关键．15．3【分析】设该圆锥的母线长为l，利用圆锥的侧面积公式得到方程，然后解方程即可求解．【详解】解：设该圆锥的母线长为l，根据题意得：，解得l=3，即该圆锥的母线长是3．故答案为：3．【点睛】本题考查了圆锥的计算：圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长．16．//【分析】以为边在y轴左侧作等边，连接，过点D作轴于点E，利用证明，得出，由垂线段最短可知，当B和E重合时，最小，则也最小，然后在，利用含的直角三角形的性质求出即可．【详解】解：以为边在y轴左侧作等边，连接，过点D作轴于点E， ，∴，，∵线段绕点A逆时针旋转至点C，∴，，∴，∴，又，，∴，∴，∴当最小时，也最小，而点B在轴上运动，由垂线段最短可知，当B和E重合时，最小值为，即的最小值为，∵，∴，∵，，∴，∴，∴的最小值为．故答案为：．【点睛】本题考查了旋转的性质，等边三角形的性质，全等三角形的判定与性质，垂线段最短，含的直角三角形的性质等知识，明确题意，添加合适辅助线，找出所求问题的条件是解题的关键．17．，见解析【分析】分别解不等式，进而得出不等式组的解集，进而得出答案．【详解】解：解不等式①，得．解不等式②，得．∴不等式组的解集为．【点睛】此题主要考查了解一元一次不等式组以及在数轴上表示不等式的解集，正确解不等式是解题关键,一元一次不等式的解法先移项，再化简（同乘除）；求一元一次不等式组解集的口诀：同大取大，同小取小，大小小大中间找，大大小小找不到（无解）．18．【分析】先根据分式的混合运算顺序和运算法则化简原式，再将m的值代入计算可得．【详解】原式＝ =，当时，原式.【点睛】本题主要考查分式的化简求值，解题的关键是掌握分式的混合运算顺序和运算法则．19．（1）见解析；（2）20％；（3）84．5分；（4）672人【分析】（1）先求出样本容量，再用用本容量减去已知各部分的频数，即可求出“90~1000”这组的频数，从而补全频数直方图；（2）用“70~80”这组的频数除以样本容量即可；（3）根据中位数的定义求解即可；（4）用1200乘以80分以上人数所占的比例即可．【详解】解：（1）8÷16％=50人，50-4-8-10-12=16人，补全频数直方图如下：（2）m==20％；（3）∵“50~80”分的人数已有22人，∴第25和26名的成绩分别是是84分，85分，∴中位数是分；（4）人．∴优秀人数是672人．【点睛】此题主要考查了频数分布直方图、扇形统计图的综合和利用统计图获取信息的能力；利用统计图获取信息时，必须认真观察、分析、研究统计图，才能作出正确的判断和解决问题．也考查了利用样本估计总体．20．(1)见解析(2) 【分析】（1）先证四边形是平行四边形，再由直角三角形斜边上的中线的性质可得，即可得证；（2）过点作于点，解直角三角形求出的长即可．【详解】（1）证明：∵，，∴四边形是平行四边形，∵，是的中点，∴，∴平行四边形是菱形；（2）解：过点作于点，如图所示，  则，∵，∴，在中，，∵，，∴，∵是的中点，∴，在中，∵，∴，∴，∴．【点睛】本题考查了菱形的判定与性质、平行四边形的判定与性质、直角三角形斜边上的中线性质等知识，熟练掌握平行四边形的判定与性质，证明四边形为菱形是解题的关键．21．(1)(2)8 【分析】（1）利用待定系数法求得反比例函数的解析式，进而求得点B的坐标，过点B作于点D，过点C作于点E，则，利用直角三角形的边角关系定理解答即可得出结论；（2）利用待定系数法求得一次函数的解析式，进而求得点A的坐标，利用点C坐标求得线段的长度，利用三角形的面积公式和的面积，将相关数值代入运算即可得出结论．【详解】（1）解：过点B作于点D，过点C作于点E，如图，设反比例函数的解析式为， ∵反比例函数的图象经过点，∴．∴反比例函数的解析式为，∵反比例函数的图象经过点，∴，∴．∴，∴；（2）∵一次函数的图象经过点B，C，∴，解得：，∴一次函数的解析式为，令，则，∴，∴．∵，∴．∴，，∴的面积．【点睛】本题主要考查了一次函数的图象与性质，一次函数图象上点的坐标的特征，反比例函数图象的性质，反比例函数图象上点的坐标的特征，待定系数法，利用点的坐标表示出相应线段的长度是解题的关键．22．(1)每台空调的价为1600元，每台电冰箱的进价为2000元(2)合适的方案共有7种，当购进电冰箱34台，空调66台获利最大，最大利润为13300元 【分析】（1）分式方程中的销售问题，题目中有两个相等关系，①每台电冰箱的进价比每台空调的进价多400元，用80000元购进电冰箱的数量与用64000元购进空调的数量相等，用第一个相等关系，设每台空调的进价为m元，表示出每台电冰箱的进价为（m+400）元，用第二个相等关系列出方程．（2）销售问题中的确定方案和利润问题，题目中有两个不等关系，①要求购进空调数量不超过电冰箱数量的2倍，②总利润不低于13000元，根据题意设出设购进电冰箱x台（x为正整数），这100台家电的销售总利润为y元，列出不等式组，确定出购买电冰箱的台数的范围，从而确定出购买方案．【详解】（1）解：设每台空调的进价为m元，则每台电冰箱的进价为（m+400）元．根据题意得：解得：经检验．是原方程的解．答：每台空调的价为1600元，每台电冰箱的进价为2000元．（2）设购进电冰箱x(x为正整数)台，这100台家电的错售总利润为y元，根据题得：解得：∵x为正整，∴x=34，35，36，37，38，39，40∴合适的方案共有7种，即①电冰箱34台，空调66台；②电冰箱35名，空调65台；③电冰箱36台；空调64台；④电冰箱37名，空调63台；⑤电冰箱38名，空调62台；⑥电冰箱39名，空调61台；⑦电冰箱40名，空调60台；∵∴y随x的增大雨减小，∴当时，y有最大值，最大值为(元)答：当购进电冰箱34台，空调66台获利最大，最大利润为13300元【点睛】本题考查了分式方程的应用、一次函数的性质以及解一元一次不等式组，解题的关键是：（1）根据数量=总价÷单价列出关于m的分式方程；（2）根据总利润=电冰箱的总利润+空调总利润找出y关于x的函数关系式．23．(1)见解析(2)①见解析；② 【分析】（1）利用基本作图，先作直径，然后过O点作的垂线即可；（2）①先根据切线的性质得到，再利用得到，接着利用等角的余角相等证明，然后利用得到；②先在中利用余弦的定义求出，则利用勾股定理计算出，再由①的结论得到，设，则，，在中利用勾股定理得到，然后解方程求出x，最后计算即可．【详解】（1）如图，为所作；（2）①证明：∵直线l与相切于点B，∴，∴，即，∵，∴，∴，∵，∴，∴，而，∴；②在中，∵，∴， ∴，∵；∴，设，则，在中，，解得，∴．【点睛】本题考查了作图-基本作图：熟练掌握5种基本作图是解决问题的关键．也考查了圆周角定理、切线的性质和解直角三角形．24．(1)(2)四边形的面积最大为，E点坐标为（－2，－1）(3)存在，P 点的坐标为（0，）或（0，） 【分析】（1）将点坐标代入，解得，即可得解；（2）先求直线的函数表达式为,设点，结合图形， 四边形的面积，运用二次函数的性质求得最值及点E点的坐标；（3）设，作于点G， ，求得＝，利用等积法得，解得n，得到点，再利用对称性得另一点【详解】（1）将代入抛物线表达式得，解得，抛物线表达式为；（2）∵抛物线的对称轴为直线，∴，，设直线的函数表达式为，将点坐标代入得，解得，∴直线的函数表达式为，..设，则，∴ ＝，∴＝，四边形的面积＋当时，四边形的面积最大，最大值为，此时E点坐标为；（3）P 点的坐标为或①作于点G， ，设， ，， ，，由的面积，得，即，化简，得，解得， （不符合题意，舍去），∴，②∵点与点P关于原点O对称， ，∴，综上所述：P 点的坐标为或）【点睛】本题为二次函数的综合应用，涉及待定系数法，三角形的面积，二次函数的性质，方程的思想及分类讨论的思想等知识，本题考点较多，综合性较强，难度适中．