2023年高考数学真题完全解读（新高考Ⅱ卷）

这是一份2023年高考数学真题完全解读（新高考Ⅱ卷），共28页。试卷主要包含了试卷总体情况分析，试题坚持思想性与科学性的统一，解答题等内容，欢迎下载使用。
2023年高考真题完全解读（新高考Ⅱ卷）
适用省份：
辽宁、重庆、海南、云南、吉林、黑龙江、安徽、山西

一、试卷总体情况分析
新高考Ⅱ卷函数与导数四个小题，一个大题，共计32分；立体几何两个小题，一个大题，共计22分；解析几何两个小题，一个大题，共计22分；三角函数与解三角形两个小题，一个大题，共计20分；统计概率两个小题，一个大题，共计22分；数列一个小题，一个大题，共计17分；集合，复数与平面向量，各占5分。总体来看，数列比重有所增加。试卷整体上提升了对学生的数学运算和逻辑推理核心素养等的考查。
二、试题坚持思想性与科学性的统一
如新课标Ⅱ卷第3题，抽样了解学生参加体育运动的情况，第19题，要求合理平衡漏诊率和误诊率，制定检测标准，试题情境既有现实意义，也能很好地体现数学学科的应用价值。全面贯彻党的教育方针，落实立德树人根本任务，促进学生德智体美劳全面发展；反映新时代基础教育课程理念，落实考试评价改革、高中育人方式改革等相关要求.
三、试题依据课程标准命题,深化基础考查
如新课标Ⅱ卷第11题，其本质是根据一元二次方程根的性质判定方程系数之间的关系，题中函数经过求导以后，其既有极大值又有极小值的性质可以转化为一元二次方程有两个正根。深入考查直观想象素养，如新课标Ⅱ卷第9题以多选题的形式考查圆锥的内容，题目全面考查基础，四个选项设问逐次递进，前面的选项为后面的选项提供了条件，各选项分别考查圆锥的不同性质，互相联系，重点突出。扎实考查数学运算素养，要求考生理解运算对象，掌握运算法则，探究运算思路，求得运算结果。如新课标Ⅱ卷第10题设置了直线与抛物线相交的情境，通过直线方程与抛物线方程的联立考查计算能力。
四．试题突出素养和能力考查，甄别思维品质
如新课标Ⅱ卷第22题将导数与三角函数巧妙的结合起来，通过对导函数的分析，考查函数的单调性、极值等相关问题，通过导数、函数不等式等知识，深入考查了分类讨论的思想，化归与转化的思想。如新课标Ⅱ卷第15题是一道开放题，有多个答案，考查直线与圆的位置关系、点到直线距离及圆内接三角形性质等知识内容。


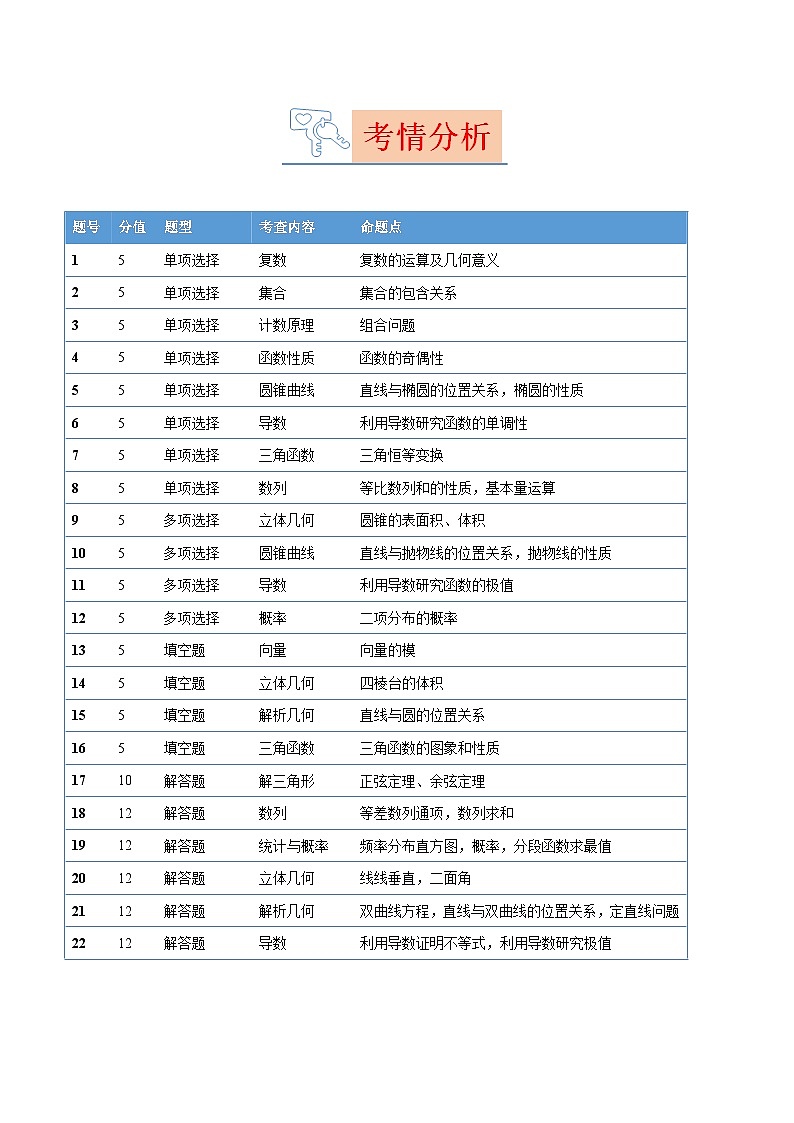
题号
分值
题型
考查内容
命题点
1
5
单项选择
复数
复数的运算及几何意义
2
5
单项选择
集合
集合的包含关系
3
5
单项选择
计数原理
组合问题
4
5
单项选择
函数性质
函数的奇偶性
5
5
单项选择
圆锥曲线
直线与椭圆的位置关系，椭圆的性质
6
5
单项选择
导数
利用导数研究函数的单调性
7
5
单项选择
三角函数
三角恒等变换
8
5
单项选择
数列
等比数列和的性质，基本量运算
9
5
多项选择
立体几何
圆锥的表面积、体积
10
5
多项选择
圆锥曲线
直线与抛物线的位置关系，抛物线的性质
11
5
多项选择
导数
利用导数研究函数的极值
12
5
多项选择
概率
二项分布的概率
13
5
填空题
向量
向量的模
14
5
填空题
立体几何
四棱台的体积
15
5
填空题
解析几何
直线与圆的位置关系
16
5
填空题
三角函数
三角函数的图象和性质
17
10
解答题
解三角形
正弦定理、余弦定理
18
12
解答题
数列
等差数列通项，数列求和
19
12
解答题
统计与概率
频率分布直方图，概率，分段函数求最值
20
12
解答题
立体几何
线线垂直，二面角
21
12
解答题
解析几何
双曲线方程，直线与双曲线的位置关系，定直线问题
22
12
解答题
导数
利用导数证明不等式，利用导数研究极值



1、减少死记硬背和‘机械刷题’现象”，扩大试题的开放性与灵活度，进一步降低死记硬背和“机械刷题”的得分收益。
2、学生应认识到低效的学习方式只会带来无效的压力和负担，讲究备考复习时效性，不断巩固阶段性复习成果。
3、你做过的题，一般不会再考——变化的是形式；高考考的题，你大部分都做过——不变的是本质；高考常换汤，偶尔换碗，永远不换的是药。数学复习过程中要重视一题多解和多题一解及变式训练，提升数学素养和解决问题的能力。


一、选择题：本大题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求的。
1．在复平面内，对应的点位于（ ）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
【答案】A
【解析】，复数对应的点位于复平面内第一象限，故选A.
【方法总结】利用复数与点的对应关系解题的步骤
(1)找对应关系：复数的几何表示法即复数z＝a＋bi(a，b∈R)可以用复平面内的点Z(a，b)来表示，是解决此类问题的根据.
(2)列出方程：此类问题可建立复数的实部与虚部应满足的条件，通过解方程(组)或不等式(组)求解.
2．设集合，，若，则（ ）．
A．2 B．1 C． D．
【答案】B
【解析】则且，此时
或且，则，显然，故选B.
【解后反思】利用集合间的关系求参数的关注点
(1)分析集合间的关系时，首先要分析、简化每个集合．
(2)此类问题通常借助数轴，利用数轴分析法，将各个集合在数轴上表示出来，以形定数，还要注意验证端点值，做到准确无误．一般含“＝”用实心点表示，不含“＝”用空心圈表示．
(3)此类问题还要注意“空集”的情况，因为空集是任何集合的子集．
3．某学校为了解学生参加体育运动的情况，用比例分配的分层随机抽样方法作抽样调查，拟从初中部和高中部两层共抽取60名学生，已知该校初中部和高中部分别有400名和200名学生，则不同的抽样结果共有（ ）．
A．种 B．种
C．种 D．种
【答案】D
【解析】初中部和高中部总共有（人），
按照分层抽样的原理，应从初中部抽取（人），
从高中部抽取（人），
第一步：从初中部抽取40人，有种方法，
第2步：从高中部抽取20人，有种方法，
根据分步计数原理，一共有种方法；故选：D.
【解题规律】有限制条件的抽(选)取问题，主要有两类
(1)“含”与“不含”问题，其解法常用直接分步法，即“含”的先取出，“不含”的可把所指元素去掉再取，分步计数．
(2)“至多”“至少”问题，其解法常有两种解决思路：一是直接分类法，但要注意分类要不重不漏；二是间接法，注意找准对立面，确保不重不漏．
4．若为偶函数，则（ ）．
A． B．0 C． D．1
【答案】B
【解析】方法一：函数的定义域为，因是偶函数，
不妨令x=1，则有
方法二：发现是奇函数，而为偶函数，
有，
故，则．选B．
【解后反思】利用奇偶性求值的常见类型 (1)求参数值：若解析式含参数，则根据f(－x)＝－f(x)或f(－x)＝f(x)列式，比较系数利用待定系数法求解；若定义域含参数，则根据定义域关于原点对称，利用区间的端点和为0求参数．
(2)求函数值：利用f(－x)＝－f(x)或f(－x)＝f(x)求解，有时需要构造奇函数或偶函数以便于求值．
5．已知椭圆的左、右焦点分别为，，直线与C交于A，B两点，若面积是面积的2倍，则（ ）．
A． B． C． D．
【答案】C

【解析】由，可得
椭圆与直线与C交于A，B两点，可得
设椭圆的左、右焦点分别为（，0），（，0）
到直线的距离分别为、，
由点到直线的距离公式可知，
因为，所以有，
即，
两边平方解得，故选C．
【解后反思】解决直线与椭圆的综合问题，要注意分类讨论思想和数形结合思想的运用
6．已知函数在区间单调递增，则a的最小值为（ ）．
A． B．e C． D．
【答案】C
【解析】函数在区间单调递增
等价于在区间上恒成立，即，
设，则在上恒有，
所以，则，即，故选C．
【解后反思】利用导数法解决取值范围问题的两个基本思路
①将问题转化为不等式在某区间上的恒成立问题，即f′(x)≥0(或f′(x)≤0)恒成立，利用分离参数或函数性质求解参数范围，然后检验参数取“＝”时是否满足题意．
②先令f′(x)>0(或f′(x)