天津市和平区部分校 2022-2023学年高一下学期期末数学试题

这是一份天津市和平区部分校 2022-2023学年高一下学期期末数学试题，文件包含天津市和平区部分校2022-2023学年高一下学期期末数学试题解析版docx、天津市和平区部分校2022-2023学年高一下学期期末数学试题原卷版docx等2份试卷配套教学资源，其中试卷共22页， 欢迎下载使用。
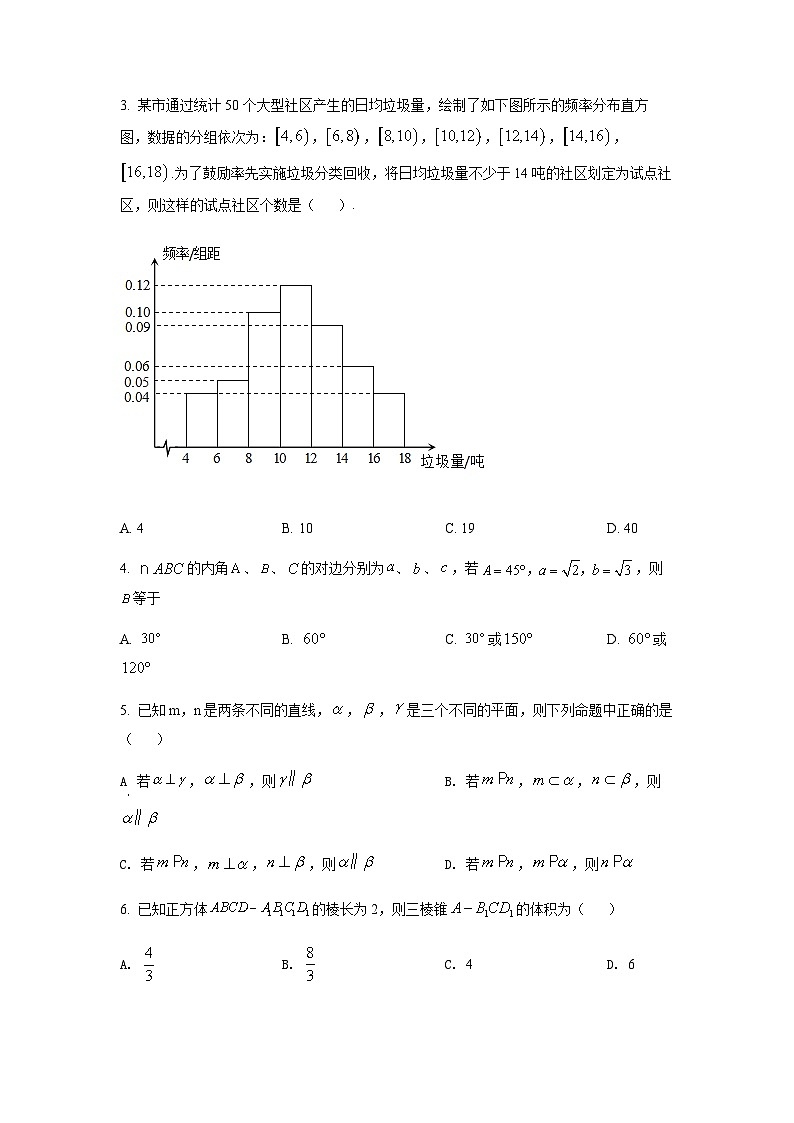
 高一数学第Ⅰ卷注意事项：1．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑．如需改动，用橡皮擦干净后，再选涂其他答案标号．2．本卷共9小题，每小题4分，共36分．参考公式：如果事件与事件互斥，那么．如果事件与事件相互独立，那么．一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的．1. 已知向量，，则A.  B.  C.  D. 【答案】A【解析】【详解】因为，所以=（5，7），故选A.考点：本小题主要考查平面向量的基本运算，属容易题. 2. 如图所示，在中，D为AB的中点，则（    ）A.  B. C.  D. 【答案】B【解析】【分析】由为的中点，可得，再利用三角形法则求解．【详解】解：在中，为的中点，，故选：B．3. 某市通过统计50个大型社区产生的日均垃圾量，绘制了如下图所示的频率分布直方图，数据的分组依次为：，，，，，，.为了鼓励率先实施垃圾分类回收，将日均垃圾量不少于14吨的社区划定为试点社区，则这样的试点社区个数是（    ）.
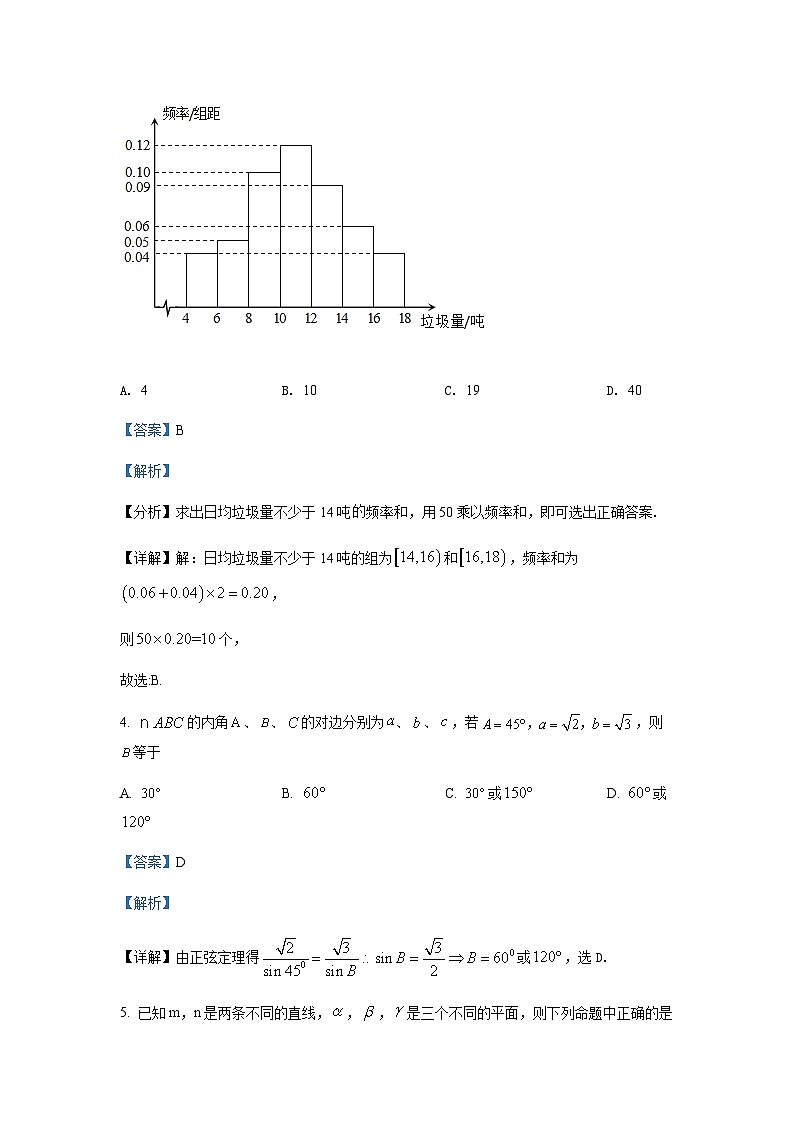
 A. 4 B. 10 C. 19 D. 40【答案】B【解析】【分析】求出日均垃圾量不少于14吨频率和，用50乘以频率和，即可选出正确答案.【详解】解：日均垃圾量不少于14吨的组为和，频率和为，则个，故选:B.4. 的内角、、的对边分别为、、，若，则等于A.  B.  C. 或 D. 或【答案】D【解析】【详解】由正弦定理得或，选D.5. 已知m，n是两条不同的直线，，，是三个不同的平面，则下列命题中正确的是（    ）A. 若，，则 B. 若，，，则C. 若，，，则 D. 若，，则【答案】C【解析】【分析】在中，与相交或平行；在中，与相交或平行；在中，由线面垂直的性质定理和面面平行的判定定理得；在中，或n在平面内.【详解】若，，则或γ与β相交，排除；若，，，则与平行或相交，排除；若，，则或n在平面内，排除.故选.【点睛】本题主要考查空间中平面与平面的位置关系、直线与平面的位置关系，解题的关键是掌握判断两平面平行和直线与平面平行的方法.6. 已知正方体的棱长为2，则三棱锥的体积为（    ）A.  B.  C. 4 D. 6【答案】B【解析】【分析】如图三棱锥是由正方体截去四个小三棱锥，从而可得答案.【详解】如图三棱锥是由正方体截去四个小三棱锥又所以故选：B7. 若是纯虚数，则实数的值等于（    ）A. 0或2 B. 2或 C.  D. 2【答案】C【解析】【分析】根据纯虚数的定义计算得解.【详解】因为是纯虚数，所以，解得；故选：C.8. 若，且，那么是（    ）A. 直角三角形 B. 等边三角形C. 非等边等腰三角形 D. 等腰直角三角形【答案】B【解析】【分析】化简，结合余弦定理可得，再利用正余弦定理对化简可得，从而可判断出的形状【详解】由，得，化简得，所以由余弦定理得，因为，所以，因为，所以由正余弦定理得，化简得，所以，所以为等边三角形，故选：B9. 在中，，，，若，则实数A.  B.  C.  D. 【答案】D【解析】【分析】将、用、表示，再代入中计算即可.【详解】由，知为的重心，所以，又，所以，，所以，.故选：D【点睛】本题考查平面向量基本定理的应用，涉及到向量的线性运算，是一道中档题.第Ⅱ卷注意事项：1．用黑色墨水的钢笔或签字笔将答案写在答题卡上．2．本卷共9小题，共64分．二、填空题：本大题共6小题，每小题4分，共24分．10. 是虚数单位，复数，则的共轭复数______.【答案】【解析】【分析】利用复数的乘法化简复数，由此可得出.【详解】，因此，.故答案为：.11. 若向量，则与平行的单位向量是________．【答案】或【解析】【分析】根据向量的坐标，可得，计算即可得出与平行的单位向量的坐标.【详解】因为，所以，则与平行的单位向量的坐标是：或，故答案为：或.12. 已知向量，，且，则坐标是___________.【答案】或【解析】【分析】根据题意可知，设，由，根据向量的模的坐标表示得出，由，得出，再根据向量垂直的坐标表示得出，即可求出和，从而求得的坐标.【详解】解：由题可知，，可设，则，由于，且，则，即：，即：，解得：或，所以的坐标是：或.故答案为：或.【点睛】本题考查平面向量坐标运算，以及向量的模和向量垂直的坐标表示，考查计算能力.13. 甲､乙两名同学进行篮球投篮练习，甲同学一次投篮命中的概率为，乙同学一次投篮命中的概率为，假设两人投篮命中与否互不影响，则甲､乙两人各投篮一次，至少有一人命中的概率是___________.【答案】【解析】【分析】考虑两个人都不命中的概率，从而可求至少有一个人命中的概率.【详解】两个都不命中的概率为，故至少有一人命中的概率是，故答案为：.14. 如图所示，一个水平放置的正方形ABCO，它在直角坐标系xOy中，点B的坐标为(2，2)，则用斜二测画法画出的正方形的直观图中，顶点B′到x′轴的距离为______.【答案】【解析】【分析】作出直观图，结合斜二测画法概率计算【详解】如图，，到轴的距离为．故答案为：．15.  是钝角三角形，内角A，B，C所对的边分别为a，b，c，，，则最大边c的取值范围是____________．【答案】【解析】【分析】由题意可得，由余弦定理结合即可求解.【详解】因为是钝角三角形，最大边为，所以角为钝角，在中，由余弦定理可得：，可得，又因为，所以，所以最大边的取值范围是：，故答案为：.三、解答题：本大题共4小题，共40分．解答应写出文字说明，证明过程或演算步骤．16. 已知中，角A，B，C的对边分别为a，b，c，，且，．（1）求a的长；（2）求的面积．【答案】（1）3    （2）【解析】【分析】（1）由已知结合正弦定理可得，然后结合余弦定理可求，.（2）先求得，再利用三角形的面积公式即可求解．【小问1详解】由结合正弦定理得，即，因为，，由余弦定理可得，，解得，，，【小问2详解】，则的面积．17. 已知某校甲、乙、丙三个年级的学生志愿者人数分别为240，160，160．现采用分层抽样的方法从中抽取7名同学去某敬老院参加献爱心活动．（1）应从甲、乙、丙三个年级的学生志愿者中分别抽取多少人?（2）设抽出的7名同学分别用A，B，C，D，E，F，G表示，现从中随机抽取2名同学承担敬老院的卫生工作．（ⅰ）若用表示样本点“抽取的2名同学为A和B”试用所给字母列举出所有可能的抽取结果；（ⅱ）设M为事件“抽取的2名同学来自同一年级”，求事件M发生的概率．【答案】（1）应从甲、乙、丙三个年级的学生志愿者中分别抽取3人，2人，2人．    （2）【解析】【分析】（1）结合人数的比值求解即可；（2）（ⅰ）由题意列出所有可能的结果即可，共有21种．（ⅱ）由题意结合（ⅰ）中的结果和古典概型计算公式求解即可【小问1详解】由已知，甲、乙、丙三个年级的学生志愿者人数之比为，由于采用分层抽样的方法从中抽取7名同学，因此应从甲、乙、丙三个年级的学生志愿者中分别抽取3人，2人，2人．【小问2详解】（ⅰ）从抽出的7名同学中随机抽取2名同学的所有可能结果为共21种．（ⅱ）由（ⅰ），不妨设抽出的7名同学中，来自甲年级的是A，B，C，来自乙年级的是D，E，来自丙年级的是F，G，则从抽出的7名同学中随机抽取的2名同学来自同一年级的所有可能结果为，共5种．所以，事件M发生的概率为P（M）=．18. 天津市某中学高三年级有1000名学生参加学情调研测试，用简单随机抽样的方法抽取了一个容量为50的样本，得到数学成绩的频率分布直方图如图所示：（1）求第四个小矩形的高，并估计本校在这次统测中数学成绩不低于120分的人数；（2）求样本数据的中位数的近似值（保留1位小数）；（3）估计这1000名学生的数学平均分．【答案】（1）0.028；700.    （2）126.7    （3）126.2【解析】【分析】（1）设第四个小矩形的高为a，由各矩形的面积之和为1求解；然后再得到数学成绩不低于120分的概率，进而得到其人数； （2）设中位数为x，利用中位数的公式求解；（3）利用平均数公式求解.【小问1详解】解：设第四个小矩形的高为a，则，解得 ，则在这次统测中数学成绩不低于120分的概率为：，所以在这次统测中数学成绩不低于120分的人数为；【小问2详解】设中位数为x，则，解得；小问3详解】这1000名学生的数学平均分为：.19.  如图，在四棱锥中，底面为平行四边形，为等边三角形，平面平面，，，，（Ⅰ）设分别为的中点，求证：平面；（Ⅱ）求证：平面；（Ⅲ）求直线与平面所成角的正弦值.【答案】（I）见解析；（II）见解析；（III）.【解析】【分析】（I）连接，结合平行四边形的性质，以及三角形中位线的性质，得到，利用线面平行的判定定理证得结果；（II）取棱的中点，连接，依题意，得，结合面面垂直的性质以及线面垂直的性质得到，利用线面垂直的判定定理证得结果；（III）利用线面角的平面角的定义得到为直线与平面所成的角，放在直角三角形中求得结果.详解】（I）证明：连接，易知，，又由，故，又因为平面，平面，所以平面.（II）证明：取棱的中点，连接，依题意，得，又因为平面平面，平面平面，所以平面，又平面，故，又已知，，所以平面.（III）解：连接，
 由（II）中平面，可知为直线与平面所成的角.因为为等边三角形，且为的中点，所以，又，在中，，所以，直线与平面所成角的正弦值为.【点睛】本小题主要考查直线与平面平行、直线与平面垂直、平面与平面垂直、直线与平面所成的角等基础知识，考查空间想象能力和推理能力.