高中数学人教A版 (2019)必修 第二册9.2 用样本估计总体课文内容课件ppt

这是一份高中数学人教A版 (2019)必修 第二册9.2 用样本估计总体课文内容课件ppt，共25页。PPT课件主要包含了2用样本估计总体，学习目标，提出问题，解决问题，画频率分布直方图，观察频率分布直方图，小试牛刀，经典例题，小结频率分布直方图，决定组距与组数等内容，欢迎下载使用。

沃德在分析问题的时候，能够做到不被表面现象所迷惑，在获取数据之后，通过数据分析，找出数据中蕴含的信息，进而得到正确的统计分析结果。
9.2.1总体取值规律的估计
基础性目标：会画出频率分布表和频率分布直方图。拓展性目标：能根据频率分布表和频率分布直方图分析具体问题。挑战性目标：结合实际，能用样本估计总体的取值规律。核心素养：数据分析、数学运算
问题1 我国是世界上严重缺水的国家之一，城市缺水问题较为突出.某市政府为了节约生活用水，计划在本市试行居民生活用水定额管理，即确定一个居民月用水量标准a，用水量不超过a的部分按平价收费，超出a的部分按议价收费. 那么标准a定为多少比较合理呢？
(1)每户居民月均用水标准a如果定得太低，会影响____________________；
(2)每户居民月均用水标准a如果定得太高，会不利于__________________；
(3)为了较为合理地确定出这个标准，需要做哪些工作？
必须先了解全市所有居民用户中，月用水量在不同范围内的居民用户所占的比例情况.
(4)如何调查全市所有居民用户的月用水量分布情况？
①全面调查：获取过去一年全市所有居民用户的月均用水量数据
②抽样调查：分析样本观测数据，估计全市居民用户月均用水量的分布情况.
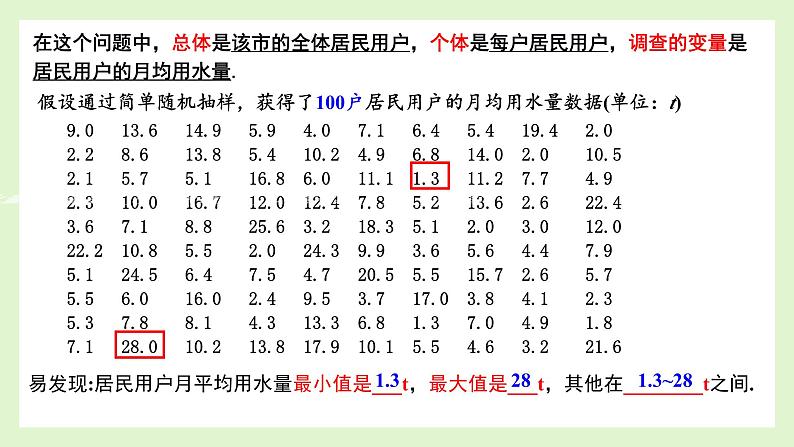
在这个问题中，总体是该市的全体居民用户，个体是每户居民用户，调查的变量是居民用户的月均用水量.
假设通过简单随机抽样，获得了100户居民用户的月均用水量数据(单位：t)
9.0 13.6 14.9 5.9 4.0 7.1 6.4 5.4 19.4 2.02.2 8.6 13.8 5.4 10.2 4.9 6.8 14.0 2.0 10.52.1 5.7 5.1 16.8 6.0 11.1 1.3 11.2 7.7 4.92.3 10.0 16.7 12.0 12.4 7.8 5.2 13.6 2.6 22.43.6 7.1 8.8 25.6 3.2 18.3 5.1 2.0 3.0 12.022.2 10.8 5.5 2.0 24.3 9.9 3.6 5.6 4.4 7.95.1 24.5 6.4 7.5 4.7 20.5 5.5 15.7 2.6 5.75.5 6.0 16.0 2.4 9.5 3.7 17.0 3.8 4.1 2.35.3 7.8 8.1 4.3 13.3 6.8 1.3 7.0 4.9 1.87.1 28.0 10.2 13.8 17.9 10.1 5.5 4.6 3.2 21.6
易发现:居民用户月平均用水量最小值是___t，最大值是___t，其他在________t之间.
分析数据的基本方法： 1.图：提取信息、传递信息. 2.表：改变数据的排列形式，提供解释数据的新方式. 在这个实际问题中，我们更关心月均用水量在不同范围内的居民用户占全市居民用户的比例.所以选择频率分布表和频率分布直方图.
频率分布：是指一组数据在各个小范围所占比例的大小，一般用频率分布表或直方图反映样本的频率分布。 频数：将一批数据按要求分为若干组，各组内的数据的个数，叫做该组数据的频数. 频率：各个小组数据在样本容量中所占的比例的大小，叫做该组数据的频率.
制作频率分布表、频率分布直方图的步骤：
1.求极差：样本数据中的最大值和最小值的差 28.0-1.3=26.72.决定组距与组数（1）组数太多或太少，都会影响我们了解数据的分布情况,组距与组数的确定没有固定的标准.（2）常当样本容量不超过100时，常分成5～12组．（3）为方便起见，一般取等长组距,并且组距应力求“取整”. 如果取组距为3，则组数= , 即可以将数据分为 组， 这也说明这个组距是比较合适的。
3.将数据分组 由于组距为3，9个组距的长度超过极差，我们可以使第一组的左端点略小于数据中的最小值1.3，最后一组的右端点略大于数据中的最大值28.0.
[1.2,4.2)，[4.2,7.2)，…，[25.2,28.2]
例如，可以取区间为 ，按如下方式把样本观测数据以组距为3，分为9组：
4.列频率分布表
建议：分组取左闭右开区间 , 最后一组取闭区间
一般分四列：分组、频数累计、 频数、频率，
横轴表示月均用水量，纵轴表示频率/组距。
各小长方形的面积的总和等于1 ，即样本数据落在整个区间的频率为1.
小长方形面积=组距×（频率/组距）=频率，
根据100户居民用户的月均用水量的频率分布，可以推测该市全体居民用户月均用水量也会有类似的分布，即大部分居民用户均用水量集中在较低值区域.
思想：用样本的频率分布估计总体的频率分布
由于样本的随机性，这种估计可能会存在一定误差
分别以3和27为组数，对数据进行等距分组，画出100户居民用户月均用水量的频率分布直方图如下图 . 观察图形，你发现不同组数对于直方图呈现数据分布规律有什么影响?
同一组数据，组数不同，得到的直方图形状和频率分布特点也不尽相同。
组数少、组距大：容易从中看出数据整体的分布特点，但损失了较多的原始数据信息，无法看出每组内的数据分布情况；
组数多、组距小：保留了较多的原始数据信息，但由于小长方形较多，图形不规则，不容易从中看出总体数据的分布特点。
不同的频率分布印象有时会影响人们对总体的判断
1.思考辨析(正确的画“√”，错误的画“×”)(1)频率分布直方图中小长方形的高表示该组上的个体在样本中出现的频率与组距的比值．(　　)(2)频率分布直方图中小矩形的面积表示该组的个体数．(　 　)2.从一堆苹果中任取10个，称得它们的质量如下(单位：克)：125，120，122，105，130，114，116，95，120，134，则样本数据落在[114.5,124.5)内的频率为(　 　)A．0.2 B．0.3 C．0.4 D．0.5
3.一个容量为80的样本中数据的最大值是140，最小值是41，组距是10，则应将样本数据分为(　　)A．10组 B．9组 C．8组 D．7组
例1 为了解中学生的身高情况，对某中学同龄的50名男生的身高进行了测量，结果如下(单位：cm)：175　168　170　176　167　181　162　173　171　177171　171　174　173　174　175　177　166　163　160166　166　163　169　174　165　175　165　170　158174　172　166　172　167　172　175　161　173　167170　172　165　157　172　173　166　177　169　181(1)列出频率分布表；(2)绘制频率分布直方图．
题型一 频率分布直方图的绘制
解： 极差为181－157＝24，将样本数据分成7组，组距为4.列频率分布表如下.
(2)绘制频率分布直方图如图．
例2 从某小区抽取100户居民进行月用电量调查，发现其用电量都在50至350度之间，频率分布直方图如图所示.(1)求直方图中x的值；(2)在这些用户中，求用电量落在区间[100,250)内的户数.
题型二 频率分布直方图的应用
解:　(1)由频率分布直方图知[200,250)小组的频率为(0.002 4＋0.0036＋0.0060＋0.0024＋0.0012+X)×50＝1，于是x＝0.0044．(2)∵数据落在[100,250)内的频率为(0.0036＋0.0060＋0.004 4)×50＝0.7，∴所求户数为0.7×100＝70．
1.求极差（一组数据中的最大值与最小值的差）.
3.将数据分组（确定分点，左闭右开最后闭）
4.列出频率分布表（分组，频数，频率）
5.列出频率分布直方图（纵轴为频率/组距）
课时练173——174页