湖北省武汉市硚口区2021-2022学年七年级下学期期末学业质量检测数学试卷(含解析)

这是一份湖北省武汉市硚口区2021-2022学年七年级下学期期末学业质量检测数学试卷(含解析)，共19页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

2021~22022 学年度第二学期期末质量检测
七年级数学试卷
一、选择题（本大题共10小题，每小题3分，共30分）
1．下列调查中，最适合采用抽样调查的是(　　)
A．对旅客上飞机前的安检 B．了解全班同学每周体育锻炼的时间
C．企业招聘，对应聘人员的面试 D．了解某批次灯泡的使用寿命情况
2．式子中，x的取值范围是（       ）
A． B． C． D．
3．若，则下列式子中错误的是（       ）
A． B． C． D．
4．点关于x轴对称的点的坐标是（       ）
A． B． C． D．
5．如图，以下说法错误的是（　　）

A．若∠EAD＝∠B，则 B．若∠BAD+∠D＝180°，则
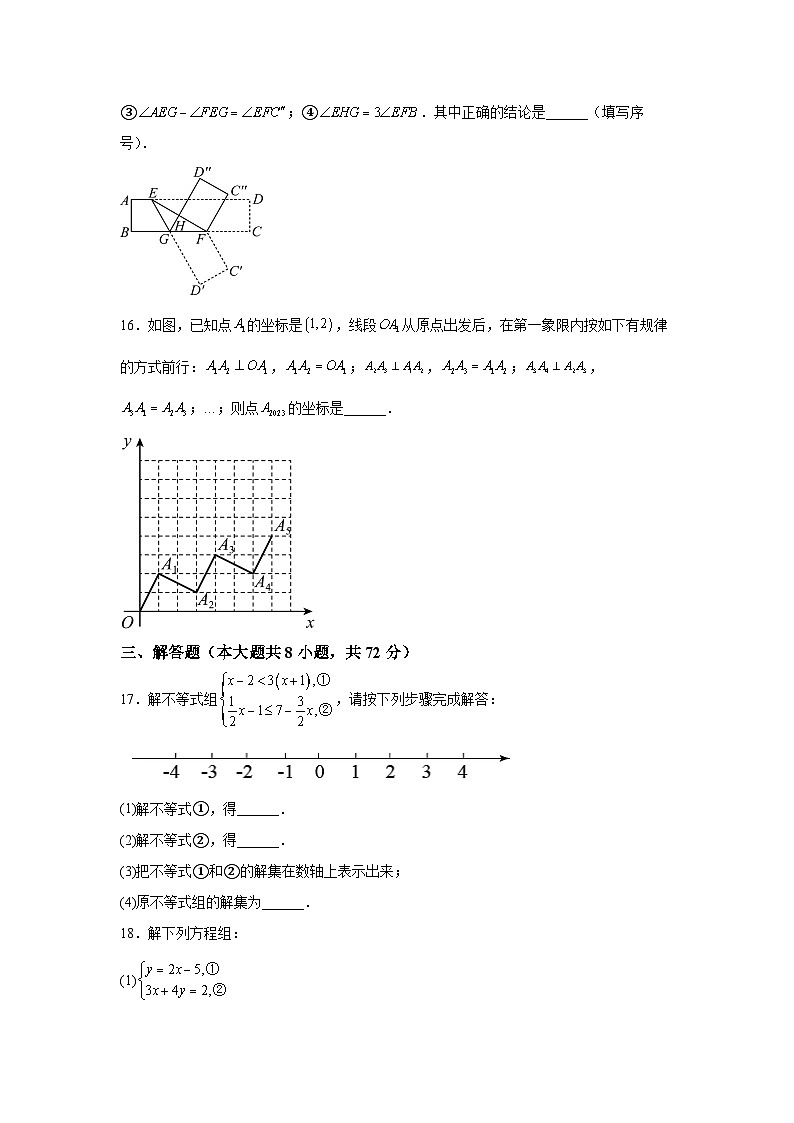
C．若∠BAC＝∠DCA，则 D．若∠D＝∠EAD，则
6．若点先向右平移个单位，再向上平移个单位，得到点，若点位于第三象限，则的取值范围是（       ）
A． B． C． D．
7．如图，，将一块等腰直角三角板的直角顶点置于直线a，b之间，已知，则的大小是（       ）

A．114° B．104° C．124° D．116°
8．用白铁皮做罐头盒，每张铁皮可制盒身25个，或制盒底40个，一个盒身与两个盒底配成一套罐头盒．现有36张白铁皮，用多少张制盒身，多少张制盒底可以使盒身与盒底正好配套？设用x张制盒身，y张制盒底，根据题意可列出的方程是（       ）
A． B． C． D．
9．若关于x的不等式组有两个整数解，则a的取值范围是（       ）
A． B． C． D．
10．某商家将蓝牙耳机、多接口优盘、迷你音箱搭配为A，B，C三种盲盒各一个，其中A盒中有2个蓝牙耳机，3个多接口优盘，1个迷你音箱；B盒中有2蓝牙耳机，4个多接口优盘，2个迷你音箱；C盒中有1个蓝牙耳机，3个多接口优盘，2个迷你音箱．经核算，A盒成本为145元，B盒成本为200元（每种盲盒的成本为该盒中蓝牙耳机、多接口优盘、迷你音箱的成本之和），则C盒的成本为（       ）
A．150元 B．155元 C．165元 D．170元
二、填空题（本大题共6小题，每小题3分，共18分）
11．计算的结果等于_________．
12．某校5名同学课外一周的体育锻炼时间（单位：小时）分别为：8，8，9，10，15．这5个数据的平均数是______．
13．关于x的不等式的解集是______．
14．现有1角，5角，1元硬币各10枚，从中共取出15枚，共值7元．则5角硬币取出了______枚．
15．如图，将长方形纸片ABCD沿EF折叠（折线EF交AD于E，交BC于F），点C，D的落点分别是，，交BC于G，再将四边形沿FG折叠，点，的落点分别是，，交EF于H．下列四个结论：①；②；③；④．其中正确的结论是______（填写序号）．

16．如图，已知点的坐标是，线段从原点出发后，在第一象限内按如下有规律的方式前行：，；，；，；…；则点的坐标是______．

三、解答题（本大题共8小题，共72分）
17．解不等式组，请按下列步骤完成解答：

(1)解不等式①，得______．
(2)解不等式②，得______．
(3)把不等式①和②的解集在数轴上表示出来；
(4)原不等式组的解集为______．
18．解下列方程组：
(1)
(2)
19．在“世界读书日”来临之际，某校为了解学生的课外阅读情况，从全校随机抽取了部分学生，调查了他们平均每周的课外阅读时间t（单位：h），整理所得数据绘制如下不完整的统计图表．
平均每周的课外阅读时间频数分布表
组别
平均每周的课外阅读时间t/h
人数
A

16
B

a
C

b
D

8

平均每周的课外阅读时间扇形统计图

根据以上图表信息，解答下列问题：
(1)这次调查的样品容量是______，______，______；
(2)B组所在扇形的圆心角的大小是______；
(3)该校共1200名学生，请你估计该校学生平均每周的课外阅读时间不少于8h的人数．
20．如图，已知，，CD与AF相交于F．

(1)求证：；
(2)若AE平分，，求的度数．
21．如图是由小正方形组成的网格，每个小正方形的顶点叫做格点，的三个顶点都是格点，其中点A的坐标是．

(1)直接写出点B，C的坐标；
(2)将先向右平移6个单位长度，再向上平移3个单位长度得，画，并写出点B的对应点的坐标；
(3)若点D是直线BC上一个动点，线段AD的最小值恰好等于线段BC的一半，写出线段AD的最小值；
(4)点M是图中网格中的格点，使的面积为3，直接写出格点M的个数．
22．某经销商购进10件A产品和20件B产品需要155元，购进20件A产品和10件B产品需要130元．A产品每件售价5元，B产品的销量不超过200件，每件8元；销量超过200件时，超过的部分每件7元．
(1)求每件A，B产品的进价；
(2)该经销商每天购进A，B产品共300件，并在当天都销售完．
①要求购进B产品的件数多于A产品件数的2倍，B产品的总利润不超过A产品总利润的4倍，设每天购进A产品x件（x为正整数），求x的取值范围；
②端午节这天，经销商让利销售，将A产品售价每件降低m元，B产品售价每件定为7元，且A，B产品的总利润的最小值不少于318元，在①中x的取值条件下，直接写出m的最大值．
23．直线，BE—EC是一条折线段，BP平分．

(1)如图1，若，求证：；
(2)CQ平分，直线BP，CQ交于点F．
①如图2，写出和的数量关系，并证明；
②当点E在直线AB，CD之间时，若，直接写出的大小．
24．在平面直角坐标系中，，，a，b满足，连接AB交y轴于C．
　　
(1)直接写出______，______；
(2)如图1，点P是y轴上一点，且三角形ABP的面积为12，求点P的坐标；
(3)如图2，直线BD交x轴于，将直线BD平移经过点A，交y轴于E，点在直线AE上，且三角形ABQ的面积不超过三角形ABD面积的，求点Q横坐标x的取值范围．


1．D
解析：
A. ∵对旅客上飞机前的安检非常重要,故宜采用普查;       
B. ∴了解全班同学每周体育锻炼的时间工作量比较小,故宜采用普查;
C. ∵企业招聘，对应聘人员的面试工作量比较小,故宜采用普查;       
D. ∵了解某批次灯泡的使用寿命情况具有破坏性, 故宜采用抽样调查;
故选D.
2．A
解析：
解：式子有意义，则x-2≥0，
解得：x≥2．
故选：A．
3．D
解析：
解：A、∵a＞b，∴a+2＞b+2，故本选项不合题意；
B、∵a＞b，∴，故本选项不合题意；
C、∵a＞b，∴a-3＞b-3，故本选项不合题意；
D、∵a＞b，∴-4a＜-4b，∴1-4a＜1-4b，故本选项符合题意．
故选：D．
4．B
解析：
解：点A（-4，2）关于x轴对称的点的坐标是（-4，-2）．
故选：B．
5．C
解析：
解：若∠EAD＝∠B，则AD∥BC，
故A说法正确，不符合题意；
若∠BAD+∠D＝180°，则AB∥CD，
故B说法正确，不符合题意；
若∠BAC＝∠DCA，则AB∥CD，
故C说法错误，符合题意；
若∠D＝∠EAD，则AB∥CD，
故D说法正确，不符合题意；
故选：C．
6．B
解析：
解：点A（n-1，n+2）先向右平移3个单位，再向上平移2个单位得到点A′（n+2，n+4），
∵点A′位于第三象限，
∴
解得，n＜-4，
故选：B．
7．A
解析：
解：如图，过直角三角板的直角顶点作直线c直线a，
∵a∥b ，
∴abc，∠3+∠4=90°，

∴∠1=∠4=24°，∠3+∠5=180°，
∴∠3=90°-∠4=66°，
∴∠5=180°-∠3=114°，
∴∠2=∠5=114°．
故选：A．
8．D
解析：
解：设用x张制盒身，y张制盒底，
可得方程组，
故选：D．
9．C
解析：
解：，
∵解不等式①得：x＜，
解不等式②得：x≥-5，
∴不等式组的解集是-5≤x＜，
∵关于x的不等式组有两个整数解，
∴-4＜≤-3，
解得：-8＜a≤-6，
故选：C．
10．B
解析：
解：设1个蓝牙耳机的价值为x元，1个多接口优盘的价值为y元，1个迷你音箱的价值为z元，
依题意得：，
②÷2得：x+2y+z=100③，
②-①得：y+z=55④，
③+④得：x+3y+2z=155，即C盒的成本为155元．
故选：B．
11．3
解析：
解：，
故答案为：3．
12．10
解析：
解：这5个数据的平均数是：×（8+8+9+10+15）=10；
故答案为：10．
13．当a＞0时，x＞2；当a＜0时，x＜2
解析：
解：ax-2a＞0（a≠0），
∴ax＞2a，
∴当a＞0时，x＞2，
当a＜0时，x＜2，
∴不等式：ax-2a＞0的解集是：当a＞0时，x＞2；当a＜0时，x＜2．
故答案为：当a＞0时，x＞2；当a＜0时，x＜2．
14．7
解析：
解：设取出1角的硬币x枚，5角的硬币y枚，则取出1元的硬币（15-x-y）枚，
依题意，得：x+5y+10（15-x-y）=70，
∴y=16-x，
∵x，y，15-x-y均为非负整数，
∴x=5，y=7，
∴15-x-y=3，
故答案为：7．
15．①③④
解析：
解：设∠GEF=x，
由折叠可知，∠GEF=∠DEF=x，
∵AD∥BC，
∴∠DEF=∠EFB=x，
∴∠GEF=∠GFE，故①正确；
∵AD∥BC，
∴∠AEF=∠EFC=180°-x，
由折叠可知，∠EFC=∠EFC'=180°-x，
∴∠GFC'180°-2x，
由折叠可知，∠GFC'=∠GFC''=180°-2x，
∴∠EFC''=180°-3x，
∵∠AEG-∠FEG=180°-2x-x=180°-3x，
∴∠AEG-∠FEG=∠EFC''，故②错误，③正确；
∵FC'∥ED'，
∴∠FGD'=180°-（180°-2x）=2x，
∵由折叠可知，∠D''GF=∠D'GF=2x，
∴∠EHG=∠D''GF+∠EFG=3x，
∴∠EHG=3∠EFB，故④正确，
故答案为：①③④．
16．（3034，1013）
解析：
解：A1（1，2），A2（3，1），A3（4，3），A4（6，2），A5（7，4），A6（9，3），…，
可得：
A1横坐标为：×3−2=1，纵坐标为：+1=2；
A3横坐标为：×3−2=4，纵坐标为：+1=3；
A5横坐标为：×3−2=7，纵坐标为：+1=4，…；
∴下标为奇数时，横坐标依次为：1，4，7，…，纵坐标为：2，3，4，…；
∴A2023横坐标为：×3−2=3034，纵坐标为：+1=1013…；
∴A2023的坐标为：（3034，1013），
故答案为：（3034，1013）．
17．(1)x＞
(2)x≤4
(3)见解析
(4)＜x≤4
18．(1)
(2)
（1）
解：，
把①代入②，得3x+4（2x-5）=2，
解得：x=2，
把x=2代入①，得y=2×2-5=-1，
所以方程组的解是；
（2）
，
②×3+③，得11x+10z=35④，
由①和④组成一个二元一次方程组，
解得：，代入②，得10+3y-2=9，
解得：y=，
所以原方程组的解是．
19．(1)80，32
(2)144°
(3)480人
（1）
解：16÷20%=80（人），
“C组”的人数为80×30%=24（人），
所以“B组”的人数为：a=80-16-24-8=32（人），
故答案为：80，32；
（2）
360°×=144°，
故答案为：144°；
（3）
1200×=480（人），
答：该校1200名学生中，平均每周的课外阅读时间不少于8h的人数大约有480人．
20．(1)见解析
(2)60°
（1）
解：证明：∵AB∥CD，
∴∠B=∠DCE，
∵∠B=∠D，
∴∠DCE=∠D，
∴AD∥BC；
（2）
∵AB∥CD，AD∥BC，
∴∠B+∠BAD=180°，∠DAE=∠E，∠B=∠DCE，
∴∠BAD=180°-∠B，
∵AE平分∠BAD，
∴∠DAE=∠BAD=90°-∠B，
∴∠E=90°-∠B，
∵∠DFE是△CEF的外角，∠DFE=2∠B，
∴∠DFE=∠E+∠DCE，
即2∠B=90°-∠B+∠B，
解得：∠B=60°．
21．(1)B（-5，1），C（-2，0
(2)画图见解析，（1，4）
(3)
(4)10
（1）
解：由图可知，B（-5，1），C（-2，0）；
（2）
如图，△A1B1C1即为所求，此时点B1的坐标为（1，4）；

（3）
由题意可得：BC=，
∵线段AD的最小值恰好等于线段BC的一半，
∴AD的最小值为BC=；
（4）
如图，点M在与BC平行的两条直线上，
∴格点M的个数为10个．
22．(1)每件A产品的进价为3.5元，每件B产品的进价为6元
(2)①≤x＜100（x为正整数）；②0.25
（1）
解：设每件A产品的进价为a元，每件B产品的进价为b元，
由题意得：，
解得：，
答：每件A产品的进价为3.5元，每件B产品的进价为6元．
（2）
①设每天购进A产品x件，则购进B产品（300-x）件，
由题意得：，
解得：≤x＜100．
∴x的取值范围为≤x＜100（x为正整数）．
②设A，B两种商品全部售完后获得的总利润为w元，则w=（5-m-3.5）x+（7-6）（300-x）=（0.5-m）x+300，
∵销售A，B两产品的总利润的最小值不少于318元，且≤x＜100，x为正整数，
∴，
解得：m≤0.25．
答：在①中x的取值条件下，m的最大值为0.25．
23．(1)见解析
(2)①∠E+2∠F=180°，证明见解析；②70°
（1）
解：证明：延长DC交BE于K，交BP于T，如图：

∵AB∥CD，
∴∠ABT=∠BTK，
∵BP平分∠ABE，
∴∠ABT=∠TBK，
∴∠BTK=∠TBK，
∵BP∥CE，
∴∠BTK=∠KCE，∠TBK=∠KEC，
∴∠KCE=∠KEC，
∵∠KCE+∠DCE=180°，
∴∠KEC+∠DCE=180°，即∠BEC+∠DCE=180°；
（2）
①∠E+2∠F=180°，证明如下：
延长AB交FQ于M，延长DC交BE于N，如图：

∵射线BP、CQ分别平分∠ABE，∠DCE，
∴∠ABP=∠EBP，∠DCQ=∠ECQ，
设∠ABP=∠EBP=α，∠DCQ=∠ECQ=β，
∴∠FBM=∠ABP=α，∠MBE=180°-2α，
∠NCE=180°-2β，∠FCN=∠DCQ=β，
∵AB∥DC，
∴∠CNE=∠MBE=180°-2α，
∴∠F=180°-∠FBM-∠FMB=180°-（α+β），
∠E=180°-∠NCE-∠CNE=180°-（180°-2β）-（180°-2α）=2（α+β）-180°，
∴∠E+180°=2（180°-∠F），
∴∠E+2∠F=180°；
②由①知∠E+2∠F=180°，
∵∠BEC=40°，
∴∠F=70°．
24．(1)-3，4
(2)-3，4
(3)-4≤x≤-2且x≠-3
解析：
（1）解：，
又∵，，
，
解得：，
故答案为：-3，4．
（2）过点作轴于，

设，
三角形的面积四边形的面积三角形的面积，
，
即，
解得：，
点的坐标为，
过点作轴于，
三角形的面积三角形的面积三角形的面积，
，
即，
，
点的坐标为或．
（3）点向左平移4个单位长度，向下平移4个单位长度到点A，
∵点D向左平移4个单位长度后的对应点正好在y轴上，
∴点平移后的对应点恰好是点，
连接，过点作轴，如图所示：

，
三角形的面积三角形的面积，
当三角形的面积三角形的面积时，，
当点在第三象限时，
，
解得：，
当点在第二象限时，
，
解得：，
当三角形的面积不超过三角形面积的时，
点的横坐标的取值范围是，且．